人教A版(2019)高中数学选择性必修第一册 【学案】第2章2.1.1倾斜角与斜率
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 【学案】第2章2.1.1倾斜角与斜率 |

|
|
| 格式 | doc | ||
| 文件大小 | 536.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览


文档简介
2.1 直线的倾斜角与斜率
2.1.1 倾斜角与斜率
学 习 目 标 核 心 素 养
1.理解直线的斜率和倾斜角的概念.(重点)2.理解直线的方向向量和向量坐标表示.(重点)3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率.(难点) 1. 通过倾斜角概念的学习,提升直观想象的数学素养.2. 通过斜率和直线方向向量的学习,培养逻辑推理和数学运算的数学素养.
看下面几个问题
[师]大家知道两点确定一条直线,那么经过一点有多少条直线?
[生]无数条.
[师]那么再给出什么条件就可确定一条呢?
[生]倾斜程度.(方向)
[师]那么我们今天就将开始学习反应直线倾斜程度的两个量——倾斜角和斜率.
1.倾斜角的相关概念
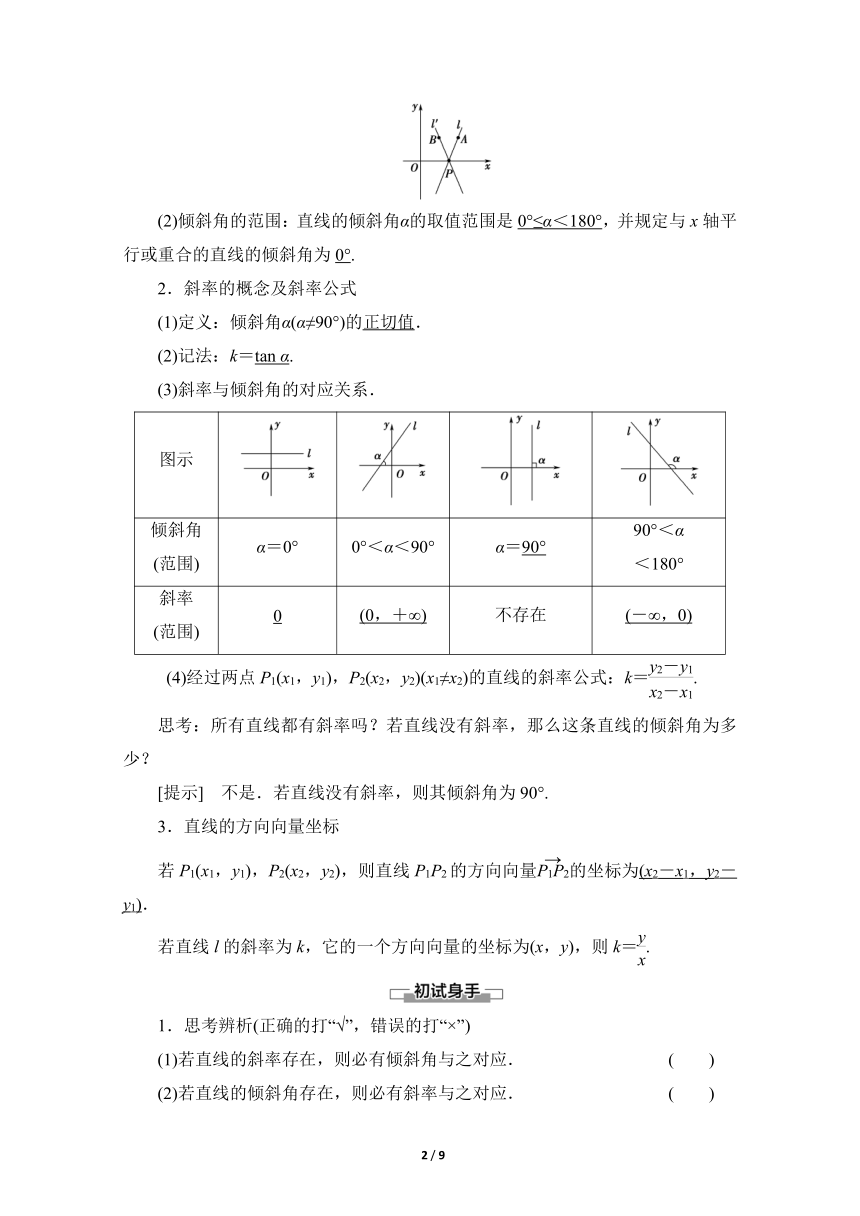
(1)倾斜角的定义:当直线l与x轴相交时,以x轴为基准,x轴正向与直线l向上的方向之间所成的角叫做直线l的倾斜角.如图所示,直线l的倾斜角是∠_APx,直线l′的倾斜角是∠BPx.
(2)倾斜角的范围:直线的倾斜角α的取值范围是0°≤α<180°,并规定与x轴平行或重合的直线的倾斜角为0°.
2.斜率的概念及斜率公式
(1)定义:倾斜角α(α≠90°)的正切值.
(2)记法:k=tan α.
(3)斜率与倾斜角的对应关系.
图示
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) 0 (0,+∞) 不存在 (-∞,0)
(4)经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式:k=.
思考:所有直线都有斜率吗?若直线没有斜率,那么这条直线的倾斜角为多少?
[提示] 不是.若直线没有斜率,则其倾斜角为90°.
3.直线的方向向量坐标
若P1(x1,y1),P2(x2,y2),则直线P1P2的方向向量的坐标为(x2-x1,y2-y1).
若直线l的斜率为k,它的一个方向向量的坐标为(x,y),则k=.
1.思考辨析(正确的打“√”,错误的打“×”)
(1)若直线的斜率存在,则必有倾斜角与之对应. ( )
(2)若直线的倾斜角存在,则必有斜率与之对应. ( )
(3)若两直线的倾斜角相等,则它们的斜率也一定相等. ( )
(4)直线的倾斜角α的集合{α|0°≤α<180°}与直线集合建立了一一对应关系. ( )
[提示] (1)√ (2)× (3)× (4)×
2.已知一条直线过点(3,-2)与点(-1,-2),则这条直线的倾斜角是( )
A.0° B.45° C.60° D.90°
A [∵k==0,∴θ =0°.]
3.已知直线l的倾斜角为30°,则直线l的斜率为( )
A. B. C.1 D.
A [由题意可知,k=tan 30°=.]
4.已知经过两点(5,m)和(m,8)的直线的斜率等于1,则m的值是________.
[由斜率公式可得=1,
解之得m=.]
直线的倾斜角
【例1】 求图中各直线的倾斜角.
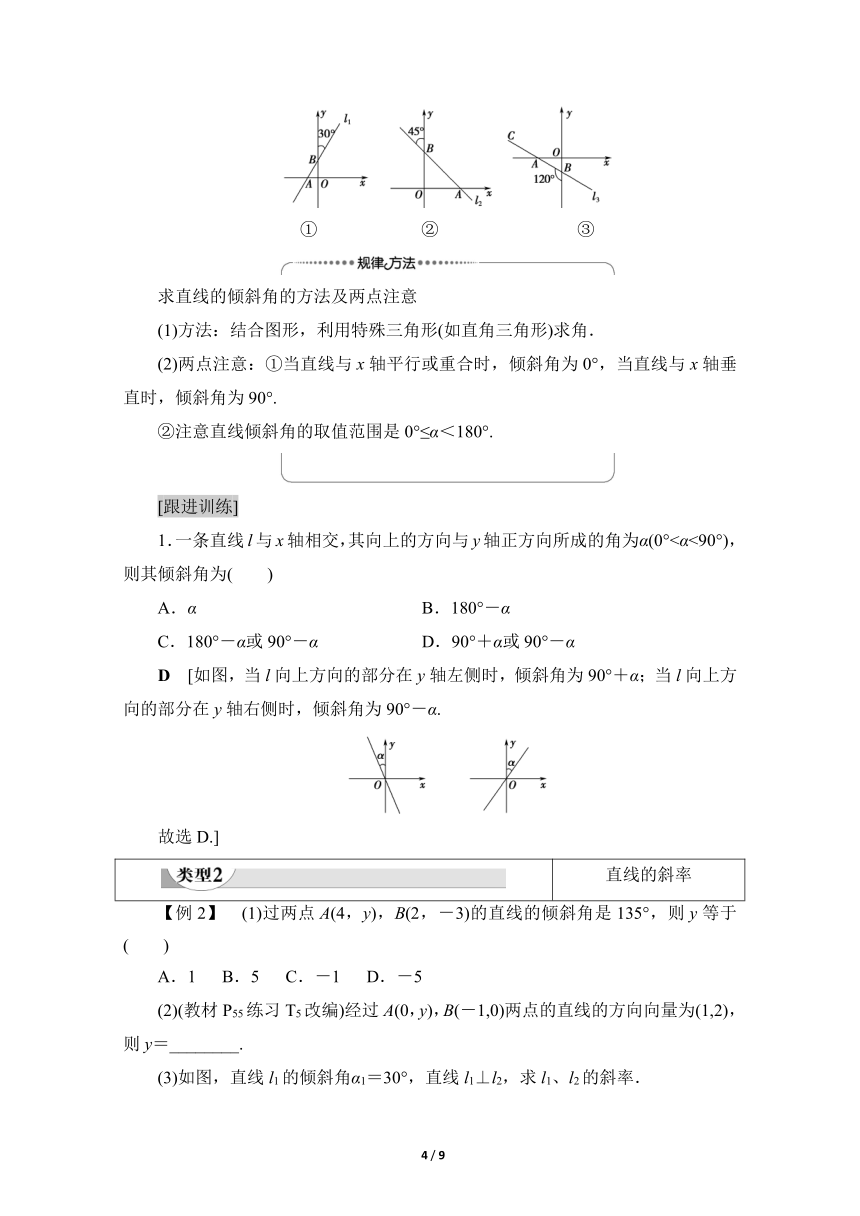
(1) (2) (3)
[解] (1)如图①,可知∠OAB为直线l1的倾斜角.易知∠ABO=30°,∴∠OAB=60°,即直线l1的倾斜角为60°.
(2)如图②,可知∠xAB为直线l2的倾斜角,易知∠OBA=45°,∴∠OAB=45°,∴∠xAB=135°,即直线l2的倾斜角为135°.
(3)如图③,可知∠OAC为直线l3的倾斜角,易知∠ABO=60°,∴∠BAO=30°,
∴∠OAC=150°,即直线l3的倾斜角为150°.
① ② ③
求直线的倾斜角的方法及两点注意
(1)方法:结合图形,利用特殊三角形(如直角三角形)求角.
(2)两点注意:①当直线与x轴平行或重合时,倾斜角为0°,当直线与x轴垂直时,倾斜角为90°.
②注意直线倾斜角的取值范围是0°≤α<180°.
[跟进训练]
1.一条直线l与x轴相交,其向上的方向与y轴正方向所成的角为α(0°<α<90°),则其倾斜角为( )
A.α B.180°-α
C.180°-α或90°-α D.90°+α或90°-α
D [如图,当l向上方向的部分在y轴左侧时,倾斜角为90°+α;当l向上方向的部分在y轴右侧时,倾斜角为90°-α.
故选D.]
直线的斜率
【例2】 (1)过两点A(4,y),B(2,-3)的直线的倾斜角是135°,则y等于( )
A.1 B.5 C.-1 D.-5
(2)(教材P55练习T5改编)经过A(0,y),B(-1,0)两点的直线的方向向量为(1,2),则y=________.
(3)如图,直线l1的倾斜角α1=30°,直线l1⊥l2,求l1、l2的斜率.
[思路探究] (1)利用公式k=(x1≠x2)=tan α;
(2)利用方向向量的共线求解;
(3)利用公式k=tan α(α≠90°).
(1)D (2)2 [(1)∵过两点A(4,y),B(2,-3)的直线的倾斜角是135°,
∴=tan 135°=-1,解得y=-5.
(2)由条件可知,直线的方向向量为(-1-0,0-y),即(-1,-y).又(1,2)是直线的另一方向向量,则=,解得y=2.]
(3)[解] 直线l1的倾斜角为α1=30°,直线l2的倾斜角α2=90°+30°=120°,
∴k=tan 30°=,k=tan 120°=-.
解决斜率问题的方法
(1)由倾斜角(或范围)求斜率(或范围)利用定义式k=tan α(α≠90°)解决.
(2)由两点坐标求斜率运用两点斜率公式k=(x1≠x2)求解.
(3)涉及直线与线段有交点问题常利用数形结合列公式求解.
[跟进训练]
2.设点A(m,-m+3),B(2,m-1),C(-1,4),直线AC的斜率等于直线BC的斜率的3倍,则实数m的值为________.
4 [依题意知,直线AC的斜率存在,且m≠-1.
kAC===-1,
kBC==,
由题意得kAC=3kBC,
∵-1=3×,解得m=4.]
直线的倾斜角和斜率的综合
[探究问题]
1.斜率公式k=中,分子与分母的顺序是否可以互换?y1与y2,x1与x2的顺序呢?
[提示] 斜率公式中分子与分母的顺序不可以互换,但y1与y2和x1与x2可以同时互换顺序,即斜率公式也可写为k=.
2.斜率的正负与倾斜角范围有什么联系?
[提示] 当k=tan α<0时, 倾斜角α是钝角;
当k=tan α>0时, 倾斜角α是锐角;
当k=tan α=0时, 倾斜角α是0°.
3.直线的斜率k随倾斜角α的增大而增大吗?
[提示] 不是,在内,k随α的增大而增大,在内,k也是随α的增大而增大.
【例3】 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.
[思路探究] 结合图形考虑,l的倾斜角应介于直线PB与直线PA的倾斜角之间,要特别注意,当l的倾斜角小于90°时,有k≥kPB;当l的倾斜角大于90°时,则有k≤kPA.
[解] 如图所示,由题意可知kPA==-1,kPB==1.
(1)要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥1.
(2)由题意可知,直线l的倾斜角介于直线PB与PA的倾斜角之间,又PB的倾斜角是45°,PA的倾斜角是135°,
所以α的取值范围是45°≤α≤135°.
1.[变条件]本例中,三点坐标不变,其它条件改为过B的直线l与线段AP有公共点,求直线l的斜率的取值范围.
[解] 如例题中图所示,
根据斜率公式得kAB==-,
kBP==1,
∴直线l的斜率的取值范围为.
2.[变条件]本例中,A、B两点坐标不变,其它条件去掉,在直线y=-1上求一点P,使PA、PB的斜率互为相反数.
[解] ∵点P在直线y=-1上,∴可设点P(x,-1).
又条件可知kPA,kPB一定存在.
由斜率公式得kPA+kPB=+=0,
解得x=.
故所求P点坐标为.
直线的倾斜角和斜率的关系
(1)直线都有倾斜角,但并不是所有的直线都有斜率.当倾斜角是90°时,直线的斜率不存在,此时,直线垂直于x轴(平行于y轴或与y轴重合).
(2)直线的斜率也反映了直线相对于x轴的正方向的倾斜程度.当0°≤α<90°时,斜率越大,直线的倾斜程度越大;当90°<α<180°时,斜率越大,直线的倾斜程度也越大.
直线的斜率和倾斜角反映了直线的倾斜程度,二者紧密相连,如下表:
直线情况 平行于x轴 垂直于x轴
α的大小 0° 0°<α<90° 90° 90°<α<180°
k的范围 0 k>0 不存在 k<0
k的增减情况 k随α的增大而增大 k随α的增大而增大
1.已知直线经过点A(0,4)和点B(1,2),则直线AB的斜率为( )
A.3 B.-2
C.2 D.不存在
B [由直线的斜率公式,得k==-2.]
2.若直线l经过第二、四象限,则直线l的倾斜角范围是( )
A.0°≤α<90° B.90°≤α<180°
C.90°<α<180° D.0°<α<180°
C [直线经过第二、四象限时,直线的倾斜角为钝角,故90°<α<180°,选C.]
3.已知直线AB与直线AC有相同的斜率,且A(1,0),B(2,a),C(a,1),则实数a的值是________.
[依题意:kAB=kAC,即=,
解得a=.]
4.已知直线l向上方向与y轴正向所成的角为30°,则直线l的倾斜角为________.
60°或120° [有如图两种情况:
① ②
第一种情况倾斜角α=90°-30°=60°,
第二种情况倾斜角α=90°+30°=120°.]
5.已知交于点M(8,6)的四条直线l1,l2,l3,l4的倾斜角之比为1∶2∶3∶4,又知l2过点N(5,3),求这四条直线的倾斜角.
[解] l2的斜率为k2==1,∴l2的倾斜角为45°,
由题意可得:l1的倾斜角为22.5°,l3的倾斜角为67.5°,l4的倾斜角为90°.
PAGE
2 / 9
2.1.1 倾斜角与斜率
学 习 目 标 核 心 素 养
1.理解直线的斜率和倾斜角的概念.(重点)2.理解直线的方向向量和向量坐标表示.(重点)3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率.(难点) 1. 通过倾斜角概念的学习,提升直观想象的数学素养.2. 通过斜率和直线方向向量的学习,培养逻辑推理和数学运算的数学素养.
看下面几个问题
[师]大家知道两点确定一条直线,那么经过一点有多少条直线?
[生]无数条.
[师]那么再给出什么条件就可确定一条呢?
[生]倾斜程度.(方向)
[师]那么我们今天就将开始学习反应直线倾斜程度的两个量——倾斜角和斜率.
1.倾斜角的相关概念
(1)倾斜角的定义:当直线l与x轴相交时,以x轴为基准,x轴正向与直线l向上的方向之间所成的角叫做直线l的倾斜角.如图所示,直线l的倾斜角是∠_APx,直线l′的倾斜角是∠BPx.
(2)倾斜角的范围:直线的倾斜角α的取值范围是0°≤α<180°,并规定与x轴平行或重合的直线的倾斜角为0°.
2.斜率的概念及斜率公式
(1)定义:倾斜角α(α≠90°)的正切值.
(2)记法:k=tan α.
(3)斜率与倾斜角的对应关系.
图示
倾斜角(范围) α=0° 0°<α<90° α=90° 90°<α<180°
斜率(范围) 0 (0,+∞) 不存在 (-∞,0)
(4)经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式:k=.
思考:所有直线都有斜率吗?若直线没有斜率,那么这条直线的倾斜角为多少?
[提示] 不是.若直线没有斜率,则其倾斜角为90°.
3.直线的方向向量坐标
若P1(x1,y1),P2(x2,y2),则直线P1P2的方向向量的坐标为(x2-x1,y2-y1).
若直线l的斜率为k,它的一个方向向量的坐标为(x,y),则k=.
1.思考辨析(正确的打“√”,错误的打“×”)
(1)若直线的斜率存在,则必有倾斜角与之对应. ( )
(2)若直线的倾斜角存在,则必有斜率与之对应. ( )
(3)若两直线的倾斜角相等,则它们的斜率也一定相等. ( )
(4)直线的倾斜角α的集合{α|0°≤α<180°}与直线集合建立了一一对应关系. ( )
[提示] (1)√ (2)× (3)× (4)×
2.已知一条直线过点(3,-2)与点(-1,-2),则这条直线的倾斜角是( )
A.0° B.45° C.60° D.90°
A [∵k==0,∴θ =0°.]
3.已知直线l的倾斜角为30°,则直线l的斜率为( )
A. B. C.1 D.
A [由题意可知,k=tan 30°=.]
4.已知经过两点(5,m)和(m,8)的直线的斜率等于1,则m的值是________.
[由斜率公式可得=1,
解之得m=.]
直线的倾斜角
【例1】 求图中各直线的倾斜角.
(1) (2) (3)
[解] (1)如图①,可知∠OAB为直线l1的倾斜角.易知∠ABO=30°,∴∠OAB=60°,即直线l1的倾斜角为60°.
(2)如图②,可知∠xAB为直线l2的倾斜角,易知∠OBA=45°,∴∠OAB=45°,∴∠xAB=135°,即直线l2的倾斜角为135°.
(3)如图③,可知∠OAC为直线l3的倾斜角,易知∠ABO=60°,∴∠BAO=30°,
∴∠OAC=150°,即直线l3的倾斜角为150°.
① ② ③
求直线的倾斜角的方法及两点注意
(1)方法:结合图形,利用特殊三角形(如直角三角形)求角.
(2)两点注意:①当直线与x轴平行或重合时,倾斜角为0°,当直线与x轴垂直时,倾斜角为90°.
②注意直线倾斜角的取值范围是0°≤α<180°.
[跟进训练]
1.一条直线l与x轴相交,其向上的方向与y轴正方向所成的角为α(0°<α<90°),则其倾斜角为( )
A.α B.180°-α
C.180°-α或90°-α D.90°+α或90°-α
D [如图,当l向上方向的部分在y轴左侧时,倾斜角为90°+α;当l向上方向的部分在y轴右侧时,倾斜角为90°-α.
故选D.]
直线的斜率
【例2】 (1)过两点A(4,y),B(2,-3)的直线的倾斜角是135°,则y等于( )
A.1 B.5 C.-1 D.-5
(2)(教材P55练习T5改编)经过A(0,y),B(-1,0)两点的直线的方向向量为(1,2),则y=________.
(3)如图,直线l1的倾斜角α1=30°,直线l1⊥l2,求l1、l2的斜率.
[思路探究] (1)利用公式k=(x1≠x2)=tan α;
(2)利用方向向量的共线求解;
(3)利用公式k=tan α(α≠90°).
(1)D (2)2 [(1)∵过两点A(4,y),B(2,-3)的直线的倾斜角是135°,
∴=tan 135°=-1,解得y=-5.
(2)由条件可知,直线的方向向量为(-1-0,0-y),即(-1,-y).又(1,2)是直线的另一方向向量,则=,解得y=2.]
(3)[解] 直线l1的倾斜角为α1=30°,直线l2的倾斜角α2=90°+30°=120°,
∴k=tan 30°=,k=tan 120°=-.
解决斜率问题的方法
(1)由倾斜角(或范围)求斜率(或范围)利用定义式k=tan α(α≠90°)解决.
(2)由两点坐标求斜率运用两点斜率公式k=(x1≠x2)求解.
(3)涉及直线与线段有交点问题常利用数形结合列公式求解.
[跟进训练]
2.设点A(m,-m+3),B(2,m-1),C(-1,4),直线AC的斜率等于直线BC的斜率的3倍,则实数m的值为________.
4 [依题意知,直线AC的斜率存在,且m≠-1.
kAC===-1,
kBC==,
由题意得kAC=3kBC,
∵-1=3×,解得m=4.]
直线的倾斜角和斜率的综合
[探究问题]
1.斜率公式k=中,分子与分母的顺序是否可以互换?y1与y2,x1与x2的顺序呢?
[提示] 斜率公式中分子与分母的顺序不可以互换,但y1与y2和x1与x2可以同时互换顺序,即斜率公式也可写为k=.
2.斜率的正负与倾斜角范围有什么联系?
[提示] 当k=tan α<0时, 倾斜角α是钝角;
当k=tan α>0时, 倾斜角α是锐角;
当k=tan α=0时, 倾斜角α是0°.
3.直线的斜率k随倾斜角α的增大而增大吗?
[提示] 不是,在内,k随α的增大而增大,在内,k也是随α的增大而增大.
【例3】 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.
[思路探究] 结合图形考虑,l的倾斜角应介于直线PB与直线PA的倾斜角之间,要特别注意,当l的倾斜角小于90°时,有k≥kPB;当l的倾斜角大于90°时,则有k≤kPA.
[解] 如图所示,由题意可知kPA==-1,kPB==1.
(1)要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥1.
(2)由题意可知,直线l的倾斜角介于直线PB与PA的倾斜角之间,又PB的倾斜角是45°,PA的倾斜角是135°,
所以α的取值范围是45°≤α≤135°.
1.[变条件]本例中,三点坐标不变,其它条件改为过B的直线l与线段AP有公共点,求直线l的斜率的取值范围.
[解] 如例题中图所示,
根据斜率公式得kAB==-,
kBP==1,
∴直线l的斜率的取值范围为.
2.[变条件]本例中,A、B两点坐标不变,其它条件去掉,在直线y=-1上求一点P,使PA、PB的斜率互为相反数.
[解] ∵点P在直线y=-1上,∴可设点P(x,-1).
又条件可知kPA,kPB一定存在.
由斜率公式得kPA+kPB=+=0,
解得x=.
故所求P点坐标为.
直线的倾斜角和斜率的关系
(1)直线都有倾斜角,但并不是所有的直线都有斜率.当倾斜角是90°时,直线的斜率不存在,此时,直线垂直于x轴(平行于y轴或与y轴重合).
(2)直线的斜率也反映了直线相对于x轴的正方向的倾斜程度.当0°≤α<90°时,斜率越大,直线的倾斜程度越大;当90°<α<180°时,斜率越大,直线的倾斜程度也越大.
直线的斜率和倾斜角反映了直线的倾斜程度,二者紧密相连,如下表:
直线情况 平行于x轴 垂直于x轴
α的大小 0° 0°<α<90° 90° 90°<α<180°
k的范围 0 k>0 不存在 k<0
k的增减情况 k随α的增大而增大 k随α的增大而增大
1.已知直线经过点A(0,4)和点B(1,2),则直线AB的斜率为( )
A.3 B.-2
C.2 D.不存在
B [由直线的斜率公式,得k==-2.]
2.若直线l经过第二、四象限,则直线l的倾斜角范围是( )
A.0°≤α<90° B.90°≤α<180°
C.90°<α<180° D.0°<α<180°
C [直线经过第二、四象限时,直线的倾斜角为钝角,故90°<α<180°,选C.]
3.已知直线AB与直线AC有相同的斜率,且A(1,0),B(2,a),C(a,1),则实数a的值是________.
[依题意:kAB=kAC,即=,
解得a=.]
4.已知直线l向上方向与y轴正向所成的角为30°,则直线l的倾斜角为________.
60°或120° [有如图两种情况:
① ②
第一种情况倾斜角α=90°-30°=60°,
第二种情况倾斜角α=90°+30°=120°.]
5.已知交于点M(8,6)的四条直线l1,l2,l3,l4的倾斜角之比为1∶2∶3∶4,又知l2过点N(5,3),求这四条直线的倾斜角.
[解] l2的斜率为k2==1,∴l2的倾斜角为45°,
由题意可得:l1的倾斜角为22.5°,l3的倾斜角为67.5°,l4的倾斜角为90°.
PAGE
2 / 9
