人教版数学八年级上册 14.2.1平方差公式 课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册 14.2.1平方差公式 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 442.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 13:27:13 | ||
图片预览







文档简介
(共20张PPT)
14.2.1 平方差公式
乘法公式
八年级上册 RJ
初中数学
知识回顾
1.单项式乘以多项式法则:
p(a+b+c)=pa+pb+pc (p,a,b,c都是单项式).
2.多项式乘以多项式法则:
(a+b)(p+q)=ap+aq+bp+bq (a,b,p,q分别是单项式).
1.了解并掌握平方差公式.
2.理解平方差公式的推导过程,并会应用平方差公式进行计算.
学习目标
课堂导入
喜洋洋在计算980×1020时,觉得这道题的计算量很大,灰太狼得意的对喜洋洋说:“你把980×1 020变成形 (1 000-20)(1 000+20)不就简单多了吗?
“你知道灰太狼运用了什么知识吗?
计算下列多项式的积:
(1) (x+1)(x-1)=_________=_____;
(2) (m+2)(m-2)=_____________=_____;
(3) (2x+1)(2x-1)=_____________=______.
x·x-x+x-1
x2 -1
m·m-2m+2m-4
m2 -4
= m2 -22
2x·2x-2x+2x-1
4x2 -1
=(2x)2 -12
观察计算结果,你能发现什么规律?
=x2 -12
猜想:(a+b)(a-b)= .
a2 -b2
知识点 平方差公式
新知探究
如何证明这个等式呢?
(1) 用多项式乘法证明
(a+b)(a-b)=
a2
-ab
+ab
-b2
=a2-b2.
(2) 借助几何图形证明
图中有两个边长分别为a,b的正方形,两个正方形的面积之差可以表示为a2- b2.
b
a
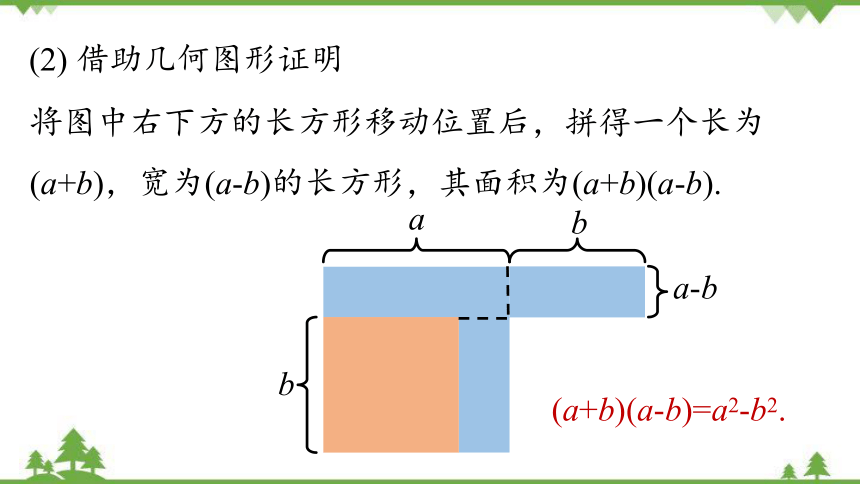
(2) 借助几何图形证明
b
a
将图中右下方的长方形移动位置后,拼得一个长为(a+b),宽为(a-b)的长方形,其面积为(a+b)(a-b).
a-b
b
(a+b)(a-b)=a2-b2.
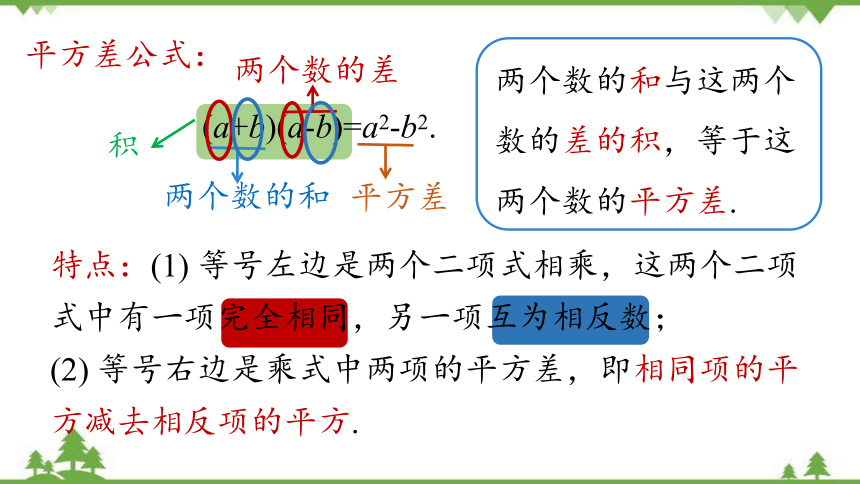
平方差公式:
(a+b)(a-b)=a2-b2.
特点:(1) 等号左边是两个二项式相乘,这两个二项式中有一项完全相同,另一项互为相反数;
(2) 等号右边是乘式中两项的平方差,即相同项的平方减去相反项的平方.
两个数的和
两个数的差
积
平方差
两个数的和与这两个数的差的积,等于这两个数的平方差.
例1 运用平方差公式计算:
(1) (3x+2)(3x-2); (2) (-x+2y)(-x-2y) .
解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.
(2) (-x+2y)(-x-2y)
=(-x)2-(2y)2
=x2-4y2 .
跟踪训练
新知探究
分析:(1) 3x相当于a,2相当于b.
(2) -x相当于a,2y相当于b.
例2 计算:
(1) (y+2)(y-2)-(y-1)(y+5); (2) 102×98.
解:(1) (y+2)(y-2)-(y-1)(y+5)
=y2-22-(y2+4y-5)
=y2-4-y2-4y+5
=-4y+1;
(2) 102×98
=(100+2)(100-2)
=1002-22
=9 996.
只有符合公式条件的乘法,才能运用公式简化运算,其余的运算仍按乘法法则进行.
平方差公式的变化及应用
变化形式 应用举例
位置变化
符号变化
系数变化
指数变化
增项变化
连用公式变化
(b+a)(-b+a)=(a+b)(a-b)=a2-b2
(-a-b)(a-b)=(-b-a)(-b+a)=(-b)2-a2=b2-a2
(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2
(a2+b2)(a2-b2)=(a2)2-(b2)2=a4-b4
(a-b+c)(a-b-c)=(a-b)2-c2
(a+b)(a-b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4
(1) 平方差公式的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式;
(2) 在运用公式时,要分清楚哪个相当于公式中的a,哪个相当于公式中的b,不要混淆.
1.(2020·郴州)如图1,将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式( )
A. x2-2x+1=(x-1)2
B. x2-1=(x+1)(x-1)
C. x2+2x+1=(x+1)2
D. x2-x=x(x-1)
x2-1
(x+1)(x-1)
B
随堂练习
2.计算下列式子:
(1) (5m+3n)(5m-3n) ; (2) (-3y-4x)(3y-4x) ;
解:(1) (5m+3n)(5n-3n)
=(5m)2-(3n)2
=25m2-9n2 ;
(2) (-3y-4x)(3y-4x)
=[(-4x)+3y][(-4x)-3y]
=(-4x)2-(3y)2
=16x2-9y2 ;
(3) (-2a2+5b)(-2a2-5b)
=(-2a2)2-(5b)2
=4a2-25b2 ;
2.计算下列式子:
(3) (-2a2+5b)(-2a2-5b) ; (4) ( x+y)(- x+y) .
3.计算下列式子:
(1) 210×190 ; (2) 2 020×2 022-2 0212 .
解:(1) 210×190
=(200+10) (200-10)
=2002-102
=40 000-100
=39 900 ;
(2) 2 020×2 022-2 0212
=(2 021-1) (2 021+1)- 2 0192
=2 0212-1-2 0212
=-1.
平方差公式
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
课堂小结
1.计算:(-3a+1) (-3a-1) (9a2+1).
解: (-3a+1) (-3a-1) (9a2+1)
= [(-3a)2-1][(3a)2+1]
=[(3a)2-1] [(3a)2+1]
=(3a)4-1
=81a4-1.
分析:观察可知,变形之后可连用两次平方差公式.
拓展提升
2.已知(a-b)2=3,(a+b)2=4,则ab= .
_________
解:因为 (a-b)2-(a+b)2
=(a-b+a+b) (a-b-a-b)
=2a· (-2b)
=-4ab,
而(a-b)2-(a+b)2=3-4=-1,
所以-4ab =-1,
所以ab= .
平方差公式的逆用
14.2.1 平方差公式
乘法公式
八年级上册 RJ
初中数学
知识回顾
1.单项式乘以多项式法则:
p(a+b+c)=pa+pb+pc (p,a,b,c都是单项式).
2.多项式乘以多项式法则:
(a+b)(p+q)=ap+aq+bp+bq (a,b,p,q分别是单项式).
1.了解并掌握平方差公式.
2.理解平方差公式的推导过程,并会应用平方差公式进行计算.
学习目标
课堂导入
喜洋洋在计算980×1020时,觉得这道题的计算量很大,灰太狼得意的对喜洋洋说:“你把980×1 020变成形 (1 000-20)(1 000+20)不就简单多了吗?
“你知道灰太狼运用了什么知识吗?
计算下列多项式的积:
(1) (x+1)(x-1)=_________=_____;
(2) (m+2)(m-2)=_____________=_____;
(3) (2x+1)(2x-1)=_____________=______.
x·x-x+x-1
x2 -1
m·m-2m+2m-4
m2 -4
= m2 -22
2x·2x-2x+2x-1
4x2 -1
=(2x)2 -12
观察计算结果,你能发现什么规律?
=x2 -12
猜想:(a+b)(a-b)= .
a2 -b2
知识点 平方差公式
新知探究
如何证明这个等式呢?
(1) 用多项式乘法证明
(a+b)(a-b)=
a2
-ab
+ab
-b2
=a2-b2.
(2) 借助几何图形证明
图中有两个边长分别为a,b的正方形,两个正方形的面积之差可以表示为a2- b2.
b
a
(2) 借助几何图形证明
b
a
将图中右下方的长方形移动位置后,拼得一个长为(a+b),宽为(a-b)的长方形,其面积为(a+b)(a-b).
a-b
b
(a+b)(a-b)=a2-b2.
平方差公式:
(a+b)(a-b)=a2-b2.
特点:(1) 等号左边是两个二项式相乘,这两个二项式中有一项完全相同,另一项互为相反数;
(2) 等号右边是乘式中两项的平方差,即相同项的平方减去相反项的平方.
两个数的和
两个数的差
积
平方差
两个数的和与这两个数的差的积,等于这两个数的平方差.
例1 运用平方差公式计算:
(1) (3x+2)(3x-2); (2) (-x+2y)(-x-2y) .
解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.
(2) (-x+2y)(-x-2y)
=(-x)2-(2y)2
=x2-4y2 .
跟踪训练
新知探究
分析:(1) 3x相当于a,2相当于b.
(2) -x相当于a,2y相当于b.
例2 计算:
(1) (y+2)(y-2)-(y-1)(y+5); (2) 102×98.
解:(1) (y+2)(y-2)-(y-1)(y+5)
=y2-22-(y2+4y-5)
=y2-4-y2-4y+5
=-4y+1;
(2) 102×98
=(100+2)(100-2)
=1002-22
=9 996.
只有符合公式条件的乘法,才能运用公式简化运算,其余的运算仍按乘法法则进行.
平方差公式的变化及应用
变化形式 应用举例
位置变化
符号变化
系数变化
指数变化
增项变化
连用公式变化
(b+a)(-b+a)=(a+b)(a-b)=a2-b2
(-a-b)(a-b)=(-b-a)(-b+a)=(-b)2-a2=b2-a2
(3a+2b)(3a-2b)=(3a)2-(2b)2=9a2-4b2
(a2+b2)(a2-b2)=(a2)2-(b2)2=a4-b4
(a-b+c)(a-b-c)=(a-b)2-c2
(a+b)(a-b)(a2+b2)=(a2-b2)(a2+b2)=a4-b4
(1) 平方差公式的字母a,b可以是单项式,也可以是多项式,只要符合这个公式的结构特征就可以运用这个公式;
(2) 在运用公式时,要分清楚哪个相当于公式中的a,哪个相当于公式中的b,不要混淆.
1.(2020·郴州)如图1,将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式( )
A. x2-2x+1=(x-1)2
B. x2-1=(x+1)(x-1)
C. x2+2x+1=(x+1)2
D. x2-x=x(x-1)
x2-1
(x+1)(x-1)
B
随堂练习
2.计算下列式子:
(1) (5m+3n)(5m-3n) ; (2) (-3y-4x)(3y-4x) ;
解:(1) (5m+3n)(5n-3n)
=(5m)2-(3n)2
=25m2-9n2 ;
(2) (-3y-4x)(3y-4x)
=[(-4x)+3y][(-4x)-3y]
=(-4x)2-(3y)2
=16x2-9y2 ;
(3) (-2a2+5b)(-2a2-5b)
=(-2a2)2-(5b)2
=4a2-25b2 ;
2.计算下列式子:
(3) (-2a2+5b)(-2a2-5b) ; (4) ( x+y)(- x+y) .
3.计算下列式子:
(1) 210×190 ; (2) 2 020×2 022-2 0212 .
解:(1) 210×190
=(200+10) (200-10)
=2002-102
=40 000-100
=39 900 ;
(2) 2 020×2 022-2 0212
=(2 021-1) (2 021+1)- 2 0192
=2 0212-1-2 0212
=-1.
平方差公式
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
课堂小结
1.计算:(-3a+1) (-3a-1) (9a2+1).
解: (-3a+1) (-3a-1) (9a2+1)
= [(-3a)2-1][(3a)2+1]
=[(3a)2-1] [(3a)2+1]
=(3a)4-1
=81a4-1.
分析:观察可知,变形之后可连用两次平方差公式.
拓展提升
2.已知(a-b)2=3,(a+b)2=4,则ab= .
_________
解:因为 (a-b)2-(a+b)2
=(a-b+a+b) (a-b-a-b)
=2a· (-2b)
=-4ab,
而(a-b)2-(a+b)2=3-4=-1,
所以-4ab =-1,
所以ab= .
平方差公式的逆用
