《志鸿全优设计》2013-2014学年高中数学人教A必修1单元目标检测:第三章 函数的应用(含解析)
文档属性
| 名称 | 《志鸿全优设计》2013-2014学年高中数学人教A必修1单元目标检测:第三章 函数的应用(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-10 00:00:00 | ||
图片预览



文档简介
数学人教A必修1第三章 函数的应用单元检测
参考完成时间:120分钟 实际完成时间:______分钟 总分:150分 得分:______
一、选择题(本大题共12小题,每小题5分,共60分)
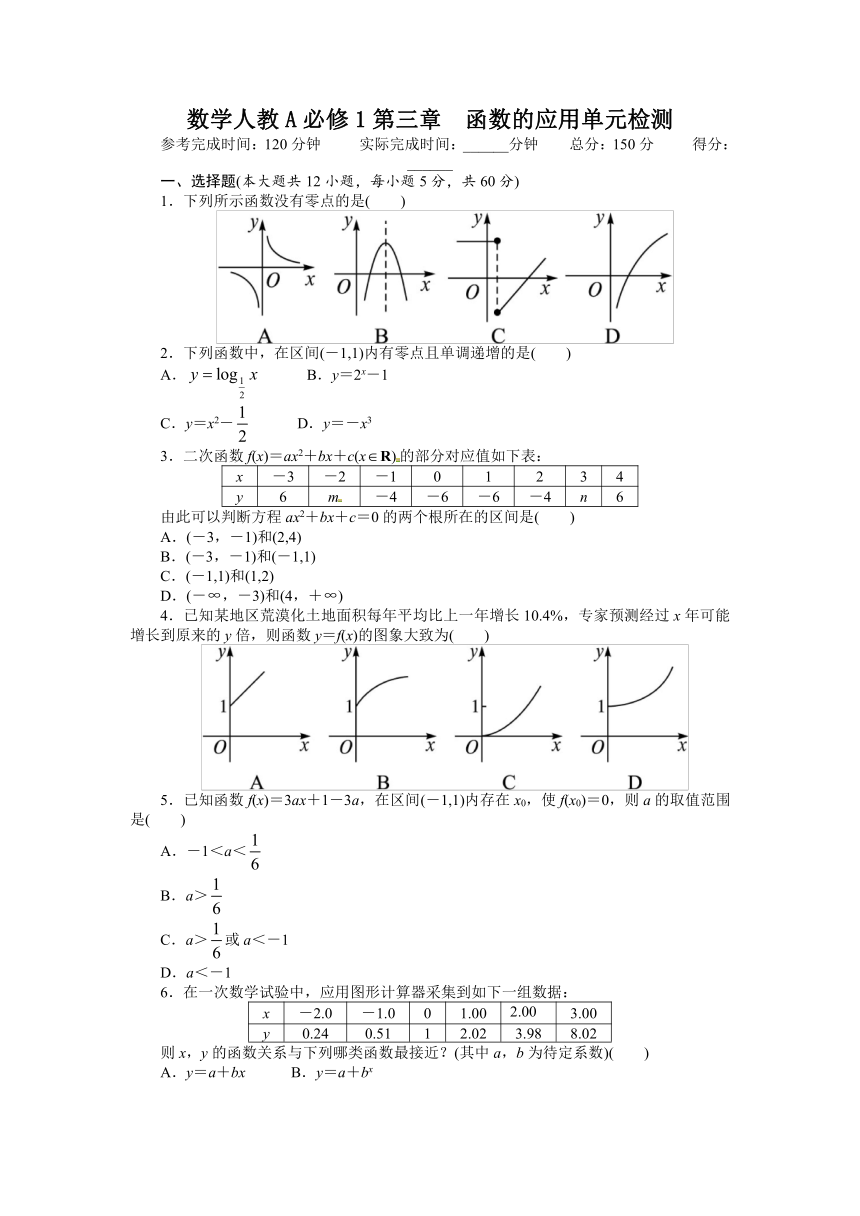
1.下列所示函数没有零点的是( )
2.下列函数中,在区间(-1,1)内有零点且单调递增的是( )
A. B.y=2x-1
C.y=x2- D.y=-x3
3.二次函数f(x)=ax2+bx+c(xR)的部分对应值如下表:
x
-3
-2
-1
0
1
2
3
4
y
6
m
-4
-6
-6
-4
n
6
由此可以判断方程ax2+bx+c=0的两个根所在的区间是( )[来源:学.科.网]
A.(-3,-1)和(2,4)
B.(-3,-1)和(-1,1)
C.(-1,1)和(1,2)
D.(-∞,-3)和(4,+∞)
4.已知某地区荒漠化土地面积每年平均比上一年增长10.4%,专家预测经过x年可能增长到原来的y倍,则函数y=f(x)的图象大致为( )
5.已知函数f(x)=3ax+1-3a,在区间(-1,1)内存在x0,使f(x0)=0,则a的取值范围是( )
A.-1<a<
B.a>
C.a>或a<-1
D.a<-1
6.在一次数学试验中,应用图形计算器采集到如下一组数据:
x
-2.0
-1.0
0
1.00
2.00[来源:学科网]
3.00
y
0.24
0.51
1
2.02
3.98
8.02
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=ax2+b D.y=a+
7.某产品的总成本y(万元)与产量x(台)之间的函数关系是y=3 000+20x-0.1x2(0<x<240,xN),若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量是( )
A.100台 B.120台
C.150台 D.180台
8.如图,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中整体水面上升高度h与注水时间t之间的函数关系大致是下列图象中的( )
9.三个变量y1,y2,y3随着变量x的变化情况如下表:
x
1
3
5
7
9
11
y1
5[来源:学&科&网]
135
625
1 715
3 635
6 655
y2
5[来源:学§科§网]
29
245
2 189
19 685
177 149
y3
5
6.10
6.61
6.95
7.20
7.40
则与x呈对数型函数、指数型函数、幂函数型函数变化的变量依次是( )
A.y1,y2,y3 B.y2,y1,y3
C.y3,y2,y1 D.y3,y1,y2
10.已知0<a<1,则方程a|x|=的实根个数为( )
A.2 B.3
C.4 D.与a的值有关
11.已知函数f(x)=-log2x,若实数x0是函数f(x)的零点,且0<x1<x0,则f(x1)的值为( )
A.恒为正值 B.等于0
C.恒为负值 D.不大于0
12.为适应社会发展的需要,国家降低某种存款利息,现有四种降息方案:①先降息p%,后降息q%;②先降息q%,后降息p%;③先降息%,再降息%;④一次性降息(p+q)%(p≠q).上述四种方案,降息最少的是( )
A.① B.②
C.③ D.④
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.用二分法求方程x3-2x-6=0在区间[1,1.5]内的一个实根,若精确度为0.01,则至少需分__________次.
14.我国GDP计划从2010年至2020年翻一番,平均每年的增长率为__________.
15.长为4,宽为3的矩形,当长增加x,宽减少时,面积达到最大,此时x的值为__________.
16.若关于x的方程在区间(0,1)上有解,则实数m的取值范围是__________.
三、解答题(本大题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)
17.(10分)求函数f(x)=2x+lg(x+1)-2的零点个数.
18.(12分)某租赁公司拥有汽车100辆,当每辆汽车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车辆会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
19.(12分)已知方程x3+2x2-3x-6=0.
(1)方程有几个实根?
(2)用二分法求出方程的最大根(精确到0.1).
20.(12分)某城市有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,但不超过40小时.设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40),在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40).
(1)求f(x)和g(x);
(2)问:小张选择哪家比较合算?为什么?
21.(12分)为了预防流感,某学校对教室用药熏消毒法消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕,y与t的函数关系为(a为常数).整个过程的图象如图所示.
(1)写出从药物释放开始,y与t的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室.从药物释放开始,至少需要几小时,学生才能回到教室?
22.(12分)经过市场调查,某商品在销售中有如下关系:第t(1≤t≤30,tN*)天的销售价格(单位:元/件)为f(t)=第t天的销售量(单位:件)为g(t)=a-t(a为常数).且在第20天该商品的销售收入为600元.(销售收入=销售价格×销售量).
(1)求a的值,并求第8天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
参考答案
1.A 点拨:A选项中的函数图象与x轴无交点.
2.B 点拨:是单调减函数;函数y=x2-在区间(-1,1)内先减后增;函数y=-x3是减函数;函数y=2x-1单调递增,且有零点x=0.
3.A 点拨:∵f(-3)=6>0,f(-1)=-4<0,
∴f(-3)·f(-1)<0.∵f(2)=-4<0,f(4)=6>0,
∴f(2)·f(4)<0.∴方程ax2+bx+c=0的两根所在的区间分别是(-3,-1)和(2,4).
4.D 点拨:设原有荒漠化土地面积为a,由题意,得y=a(1+10.4%)x.故其图象应如D项中图所示,选D.
5.B 点拨:由题意,得f(-1)·f(1)<0,即(-3a+1-3a)×1<0,也即1-6a<0.故a>.
6.B 点拨:代入数据检验,注意函数值.
7.C 点拨:由题意知
即
解得150≤x<240且xN.
故生产者不亏本时的最低产量为150台.
8.B 点拨:开始一段时间,水槽底部没有水,烧杯满了之后,水槽中水面上升先快后慢.故选B.
9.C 点拨:三种常见增长型函数中,指数型函数呈爆炸性增长,而对数型函数增长越来越慢,幂函数型函数介于两者之间,结合题表,只有C项中数据符合上述规律.
10.A 点拨:设y1=a|x|,y2=|logax|,分别作出这两个函数的图象,如下图所示.
由图可知,有两个交点,故方程a|x|=|logax|有两个实根,应选A.
11.A 点拨:∵函数f(x)在区间(0,+∞)上为减函数,且f(x0)=0,∴当x(0,x0)时,均有f(x)>0.又∵0<x1<x0,
∴f(x1)>0.
12.C 点拨:方法1:特例法,不妨取p=20,q=40,验证即可.方法2:作差比较.
13.6 点拨:设需分n次,据题意,有<0.01=,即2n>50.因此n最小取6,即至少需分6次.
14.7.18% 点拨:设平均每年增长率为x,
则2=(1+p)10.
∴1+p=≈1.071 8.∴p≈0.071 8.
15.1 点拨:由题意知S=(4+x) ,即S=+x+12,因此当x=1时,S最大.
16.0<m<1 点拨:要使方程有解,只需在函数y=(0<x<1)的值域内,即>0.[来源:学科网]
∵x(0,1),∴>0.
∴>0.∴0<m<1.
17.解法一:∵f(0)=1+0-2=-1<0,f(2)=4+lg 3-2=2+lg 3>0,
∴函数f(x)在区间(0,2)上必定存在零点.
又f(x)=2x+lg(x+1)-2在区间(-1,+∞)上为增函数,故函数f(x)有且只有一个零点.
解法二:在同一坐标系内作出函数h(x)=2-2x和g(x)=lg(x+1)的图象,如图所示.由图象知y=lg(x+1)和y=2-2x有且只有一个交点,即f(x)=2x+lg(x+1)-2有且只有一个零点.
18.解:(1)当每辆车的月租金定为3 600元时,
∵3 600-3 000=600(元),100-=88(辆),
∴此时能租出88辆车.
(2)设每辆车的月租金定为x(3 000≤x<5 000)元时,租赁公司的月收益为y元,则
y=·50=+162x-21 000=(x-4 050)2+307 050,
因此x=4 050时,函数有最大值307 050.
故当每辆车的月租金定为4 050元时,租赁公司的月收益最大为307 050元.
19.解:(1)令f(x)=x3+2x2-3x-6.
∵f(-3)=(-3)3+2×(-3)2-3×(-3)-6=-6<0,
f(-2)=(-2)3+2×(-2)2-3×(-2)-6=0,
f(-1)=(-1)3+2×(-1)2-3×(-1)-6=-2<0,
f(0)=-6<0,
f(1)=1+2-3-6=-6<0,
f(2)=23+2×22-3×2-6=4>0,
又f(-1.9)=(-1.9)3+2×(-1.9)2-3×(-1.9)-6=0.061>0,
∴方程有3个实根,且分别处在下面三个区间内:
(-3,-1.9),(-1.9,-1),(1,2).
(2)由(1)知方程最大的根处在区间(1,2)内,用二分法逐次计算,列表如下:
∵最后一个区间两个端点精确到0.1的近似值都是1.7,
∴所求方程的最大根约为1.7.
20.解:(1)f(x)=5x(15≤x≤40);
g(x)=
(2)由f(x)=g(x),得或
即x=18或x=10(舍).
当15≤x<18时,f(x)-g(x)=5x-90<0,
即f(x)<g(x),应选甲家;
当x=18时,f(x)=g(x),即可以选甲家也可以选乙家.
当18<x≤30时,f(x)-g(x)=5x-90>0,
即f(x)>g(x),应选乙家.
当30<x≤40时,
f(x)-g(x)=5x-(2x+30)=3x-30>0,
即f(x)>g(x),应选乙家.
综上所述:当15≤x<18时,选甲家;
当x=18时,可以选甲家也可以选乙家;
当18<x≤40时,选乙家.
21.解:(1)由题意及图象可知,当0≤t≤0.1时,可设y=kt.
∵当t=0.1时,y=1,∴0.1k=1,k=10.故y=10t.
当t>0.1时,由t=0.1,y=1,得,∴a=0.1.
∴y与t的函数关系式为y=
(2)由题意,得≤0.25,即2-4(t-0.1)≤2-2,从而可得-4(t-0.1)≤-2,解得t≥0.6.
故至少经过0.6小时后,学生方可回到教室.
22.解:(1)当t=20时,f(20)=30,g(20)=a-20,
由f(20)g(20)=30(a-20)=600,
解得a=40.
从而可得,f(8)g(8)=38×32=1 216(元),
即第8天该商品的销售收入为1 216元.
(2)依题意
当1≤t<10时,y=(40-t)(30+t)=-t2+10t+1 200=-(t-5)2+1 225,
所以t=5时,y取得最大值1 225元.
当10≤t≤30时,y=(40-t)(50-t)=t2-90t+2 000=(t-45)2-25,
因为t[10,30]时,函数为减函数,
所以t=10时,y取得最大值1 200元.
故当t=5时,该商品日销售收入最大,最大值为1 225元.
参考完成时间:120分钟 实际完成时间:______分钟 总分:150分 得分:______
一、选择题(本大题共12小题,每小题5分,共60分)
1.下列所示函数没有零点的是( )
2.下列函数中,在区间(-1,1)内有零点且单调递增的是( )
A. B.y=2x-1
C.y=x2- D.y=-x3
3.二次函数f(x)=ax2+bx+c(xR)的部分对应值如下表:
x
-3
-2
-1
0
1
2
3
4
y
6
m
-4
-6
-6
-4
n
6
由此可以判断方程ax2+bx+c=0的两个根所在的区间是( )[来源:学.科.网]
A.(-3,-1)和(2,4)
B.(-3,-1)和(-1,1)
C.(-1,1)和(1,2)
D.(-∞,-3)和(4,+∞)
4.已知某地区荒漠化土地面积每年平均比上一年增长10.4%,专家预测经过x年可能增长到原来的y倍,则函数y=f(x)的图象大致为( )
5.已知函数f(x)=3ax+1-3a,在区间(-1,1)内存在x0,使f(x0)=0,则a的取值范围是( )
A.-1<a<
B.a>
C.a>或a<-1
D.a<-1
6.在一次数学试验中,应用图形计算器采集到如下一组数据:
x
-2.0
-1.0
0
1.00
2.00[来源:学科网]
3.00
y
0.24
0.51
1
2.02
3.98
8.02
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx
C.y=ax2+b D.y=a+
7.某产品的总成本y(万元)与产量x(台)之间的函数关系是y=3 000+20x-0.1x2(0<x<240,xN),若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量是( )
A.100台 B.120台
C.150台 D.180台
8.如图,向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中整体水面上升高度h与注水时间t之间的函数关系大致是下列图象中的( )
9.三个变量y1,y2,y3随着变量x的变化情况如下表:
x
1
3
5
7
9
11
y1
5[来源:学&科&网]
135
625
1 715
3 635
6 655
y2
5[来源:学§科§网]
29
245
2 189
19 685
177 149
y3
5
6.10
6.61
6.95
7.20
7.40
则与x呈对数型函数、指数型函数、幂函数型函数变化的变量依次是( )
A.y1,y2,y3 B.y2,y1,y3
C.y3,y2,y1 D.y3,y1,y2
10.已知0<a<1,则方程a|x|=的实根个数为( )
A.2 B.3
C.4 D.与a的值有关
11.已知函数f(x)=-log2x,若实数x0是函数f(x)的零点,且0<x1<x0,则f(x1)的值为( )
A.恒为正值 B.等于0
C.恒为负值 D.不大于0
12.为适应社会发展的需要,国家降低某种存款利息,现有四种降息方案:①先降息p%,后降息q%;②先降息q%,后降息p%;③先降息%,再降息%;④一次性降息(p+q)%(p≠q).上述四种方案,降息最少的是( )
A.① B.②
C.③ D.④
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.用二分法求方程x3-2x-6=0在区间[1,1.5]内的一个实根,若精确度为0.01,则至少需分__________次.
14.我国GDP计划从2010年至2020年翻一番,平均每年的增长率为__________.
15.长为4,宽为3的矩形,当长增加x,宽减少时,面积达到最大,此时x的值为__________.
16.若关于x的方程在区间(0,1)上有解,则实数m的取值范围是__________.
三、解答题(本大题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤)
17.(10分)求函数f(x)=2x+lg(x+1)-2的零点个数.
18.(12分)某租赁公司拥有汽车100辆,当每辆汽车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车辆会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
19.(12分)已知方程x3+2x2-3x-6=0.
(1)方程有几个实根?
(2)用二分法求出方程的最大根(精确到0.1).
20.(12分)某城市有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,但不超过40小时.设在甲家租一张球台开展活动x小时的收费为f(x)元(15≤x≤40),在乙家租一张球台开展活动x小时的收费为g(x)元(15≤x≤40).
(1)求f(x)和g(x);
(2)问:小张选择哪家比较合算?为什么?
21.(12分)为了预防流感,某学校对教室用药熏消毒法消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕,y与t的函数关系为(a为常数).整个过程的图象如图所示.
(1)写出从药物释放开始,y与t的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进入教室.从药物释放开始,至少需要几小时,学生才能回到教室?
22.(12分)经过市场调查,某商品在销售中有如下关系:第t(1≤t≤30,tN*)天的销售价格(单位:元/件)为f(t)=第t天的销售量(单位:件)为g(t)=a-t(a为常数).且在第20天该商品的销售收入为600元.(销售收入=销售价格×销售量).
(1)求a的值,并求第8天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
参考答案
1.A 点拨:A选项中的函数图象与x轴无交点.
2.B 点拨:是单调减函数;函数y=x2-在区间(-1,1)内先减后增;函数y=-x3是减函数;函数y=2x-1单调递增,且有零点x=0.
3.A 点拨:∵f(-3)=6>0,f(-1)=-4<0,
∴f(-3)·f(-1)<0.∵f(2)=-4<0,f(4)=6>0,
∴f(2)·f(4)<0.∴方程ax2+bx+c=0的两根所在的区间分别是(-3,-1)和(2,4).
4.D 点拨:设原有荒漠化土地面积为a,由题意,得y=a(1+10.4%)x.故其图象应如D项中图所示,选D.
5.B 点拨:由题意,得f(-1)·f(1)<0,即(-3a+1-3a)×1<0,也即1-6a<0.故a>.
6.B 点拨:代入数据检验,注意函数值.
7.C 点拨:由题意知
即
解得150≤x<240且xN.
故生产者不亏本时的最低产量为150台.
8.B 点拨:开始一段时间,水槽底部没有水,烧杯满了之后,水槽中水面上升先快后慢.故选B.
9.C 点拨:三种常见增长型函数中,指数型函数呈爆炸性增长,而对数型函数增长越来越慢,幂函数型函数介于两者之间,结合题表,只有C项中数据符合上述规律.
10.A 点拨:设y1=a|x|,y2=|logax|,分别作出这两个函数的图象,如下图所示.
由图可知,有两个交点,故方程a|x|=|logax|有两个实根,应选A.
11.A 点拨:∵函数f(x)在区间(0,+∞)上为减函数,且f(x0)=0,∴当x(0,x0)时,均有f(x)>0.又∵0<x1<x0,
∴f(x1)>0.
12.C 点拨:方法1:特例法,不妨取p=20,q=40,验证即可.方法2:作差比较.
13.6 点拨:设需分n次,据题意,有<0.01=,即2n>50.因此n最小取6,即至少需分6次.
14.7.18% 点拨:设平均每年增长率为x,
则2=(1+p)10.
∴1+p=≈1.071 8.∴p≈0.071 8.
15.1 点拨:由题意知S=(4+x) ,即S=+x+12,因此当x=1时,S最大.
16.0<m<1 点拨:要使方程有解,只需在函数y=(0<x<1)的值域内,即>0.[来源:学科网]
∵x(0,1),∴>0.
∴>0.∴0<m<1.
17.解法一:∵f(0)=1+0-2=-1<0,f(2)=4+lg 3-2=2+lg 3>0,
∴函数f(x)在区间(0,2)上必定存在零点.
又f(x)=2x+lg(x+1)-2在区间(-1,+∞)上为增函数,故函数f(x)有且只有一个零点.
解法二:在同一坐标系内作出函数h(x)=2-2x和g(x)=lg(x+1)的图象,如图所示.由图象知y=lg(x+1)和y=2-2x有且只有一个交点,即f(x)=2x+lg(x+1)-2有且只有一个零点.
18.解:(1)当每辆车的月租金定为3 600元时,
∵3 600-3 000=600(元),100-=88(辆),
∴此时能租出88辆车.
(2)设每辆车的月租金定为x(3 000≤x<5 000)元时,租赁公司的月收益为y元,则
y=·50=+162x-21 000=(x-4 050)2+307 050,
因此x=4 050时,函数有最大值307 050.
故当每辆车的月租金定为4 050元时,租赁公司的月收益最大为307 050元.
19.解:(1)令f(x)=x3+2x2-3x-6.
∵f(-3)=(-3)3+2×(-3)2-3×(-3)-6=-6<0,
f(-2)=(-2)3+2×(-2)2-3×(-2)-6=0,
f(-1)=(-1)3+2×(-1)2-3×(-1)-6=-2<0,
f(0)=-6<0,
f(1)=1+2-3-6=-6<0,
f(2)=23+2×22-3×2-6=4>0,
又f(-1.9)=(-1.9)3+2×(-1.9)2-3×(-1.9)-6=0.061>0,
∴方程有3个实根,且分别处在下面三个区间内:
(-3,-1.9),(-1.9,-1),(1,2).
(2)由(1)知方程最大的根处在区间(1,2)内,用二分法逐次计算,列表如下:
∵最后一个区间两个端点精确到0.1的近似值都是1.7,
∴所求方程的最大根约为1.7.
20.解:(1)f(x)=5x(15≤x≤40);
g(x)=
(2)由f(x)=g(x),得或
即x=18或x=10(舍).
当15≤x<18时,f(x)-g(x)=5x-90<0,
即f(x)<g(x),应选甲家;
当x=18时,f(x)=g(x),即可以选甲家也可以选乙家.
当18<x≤30时,f(x)-g(x)=5x-90>0,
即f(x)>g(x),应选乙家.
当30<x≤40时,
f(x)-g(x)=5x-(2x+30)=3x-30>0,
即f(x)>g(x),应选乙家.
综上所述:当15≤x<18时,选甲家;
当x=18时,可以选甲家也可以选乙家;
当18<x≤40时,选乙家.
21.解:(1)由题意及图象可知,当0≤t≤0.1时,可设y=kt.
∵当t=0.1时,y=1,∴0.1k=1,k=10.故y=10t.
当t>0.1时,由t=0.1,y=1,得,∴a=0.1.
∴y与t的函数关系式为y=
(2)由题意,得≤0.25,即2-4(t-0.1)≤2-2,从而可得-4(t-0.1)≤-2,解得t≥0.6.
故至少经过0.6小时后,学生方可回到教室.
22.解:(1)当t=20时,f(20)=30,g(20)=a-20,
由f(20)g(20)=30(a-20)=600,
解得a=40.
从而可得,f(8)g(8)=38×32=1 216(元),
即第8天该商品的销售收入为1 216元.
(2)依题意
当1≤t<10时,y=(40-t)(30+t)=-t2+10t+1 200=-(t-5)2+1 225,
所以t=5时,y取得最大值1 225元.
当10≤t≤30时,y=(40-t)(50-t)=t2-90t+2 000=(t-45)2-25,
因为t[10,30]时,函数为减函数,
所以t=10时,y取得最大值1 200元.
故当t=5时,该商品日销售收入最大,最大值为1 225元.
