2013最新人教版八年级上数学第13章轴对称全章导学案
文档属性
| 名称 | 2013最新人教版八年级上数学第13章轴对称全章导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 450.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-10 00:00:00 | ||
图片预览



文档简介
姓名: 班级: 成绩:
13.1 轴对称学案(一)
(一)、预习课本P58---P60,完成下面的习题
(二)、概念:
(1)轴对称图形:如果一个图形沿一条 折叠,直线两旁的部分能够 ,这个图形就叫做 。这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线 。
(2)轴对称:把一个图形沿着某一条直线折叠,如果它能够与 重合,那么就说这两个图形关于这条直线成 。这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重叠的点)叫做 。
(3)轴对称图形和两个图形成轴对称有什么区别和联系?
区别: 轴对称是说 个图形的位置关系,
轴对称图形是说 个具有特殊形状的图形。
联系:都能沿着某条直线 。这条直线是对称轴。
(三)、思考:
(1)成轴对称的两个图形全等吗 全等的两个图形一定成轴对称吗?
(2)如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成 ;反过来,如果把两个成轴对称的图形看成一个整体,那么它就是一个 图形.
(四)、练一练:
1、标出下列图形中的对称点
2、下面给出的每幅图中的两个图案是轴对称的吗?如果是,试着找画它们的对称轴,并找出一对对称点.
3.等腰三角形的对称轴有( )
A、1条 B、3条 C、1条或3条 D、无数条
4.下列图形中不是轴对称图形的是( )
A B C D
5. 下列图案是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
6.下列英文字母属于轴对称图形的是( )
A、N B、S C、L D、E
7.下列各时刻是轴对称图形的为( )
A、 B、 C、 D、
8.如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是( ),折痕所在的直线叫做( )。
9.在对称图形中,对称轴两侧相对应的点到对称轴的( )。
10.( )三角形有三条对称轴,( )三角形有一条对称轴。
11.正方形有( )条对称轴,长方形有( )条对称轴,等腰梯形有( )条对称轴。
12.判断。
①.通过一个圆的圆心的直线是这个圆的对称轴。 ( )
②.圆是轴对称图形,每一条直径都是它的对称轴。( )
③.等腰梯形是对称图形。 ( )
④.正方形只有一条对称轴。 ( )
13.请写出下列图形的对称轴的条数
① 等边三角形 ② 正方形 ③ 圆
④ 长方形 ⑤平行四边形 ⑥正六边形
14.当写着数字的纸条垂直于镜面摆放时(如图所示):
下面是从镜子中看到的数: ,它实际上是________________
16.作图题,画下面图形的对称轴.
13.1.2线段垂直平分线性质定理
一、知识链接:
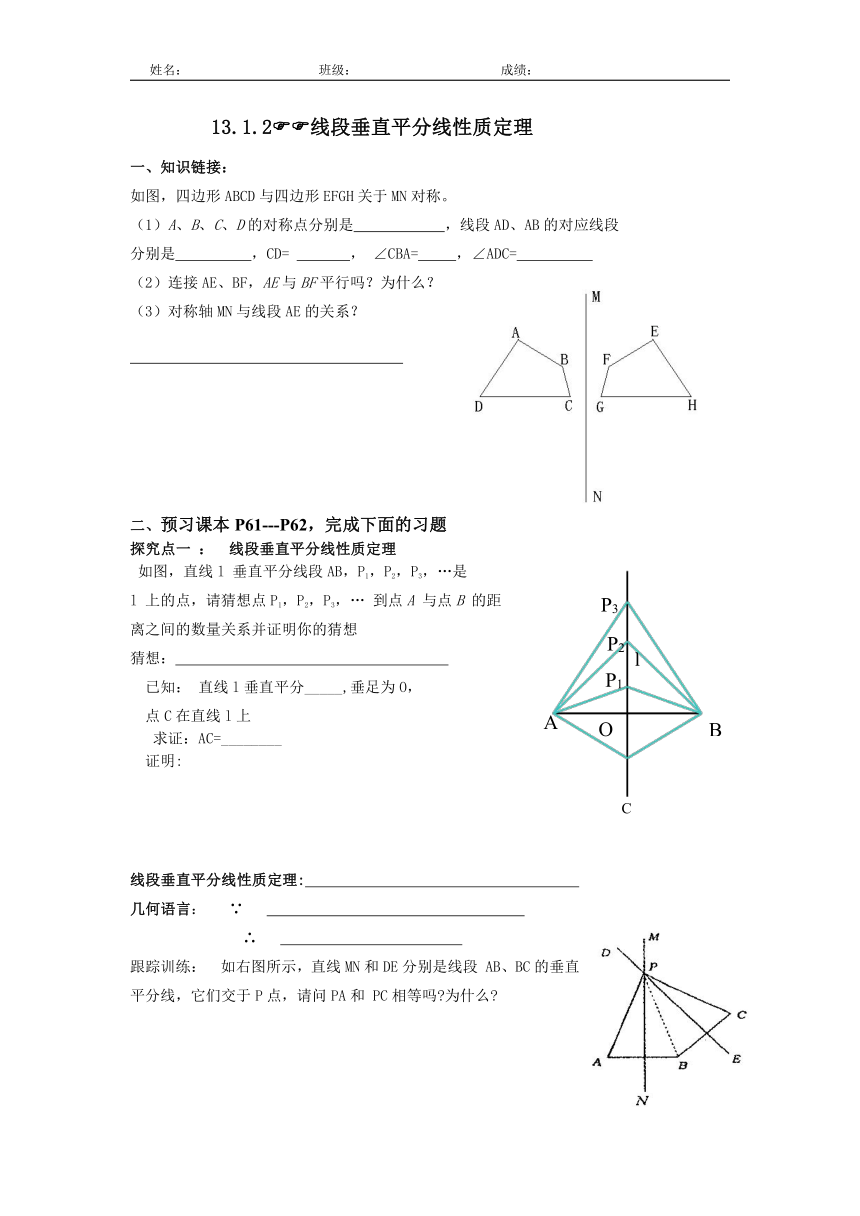
如图,四边形ABCD与四边形EFGH关于MN对称。
(1)A、B、C、D的对称点分别是 ,线段AD、AB的对应线段
分别是 ,CD= , ∠CBA= ,∠ADC=
(2)连接AE、BF,AE与BF平行吗?为什么?
(3)对称轴MN与线段AE的关系?
二、预习课本P61---P62,完成下面的习题
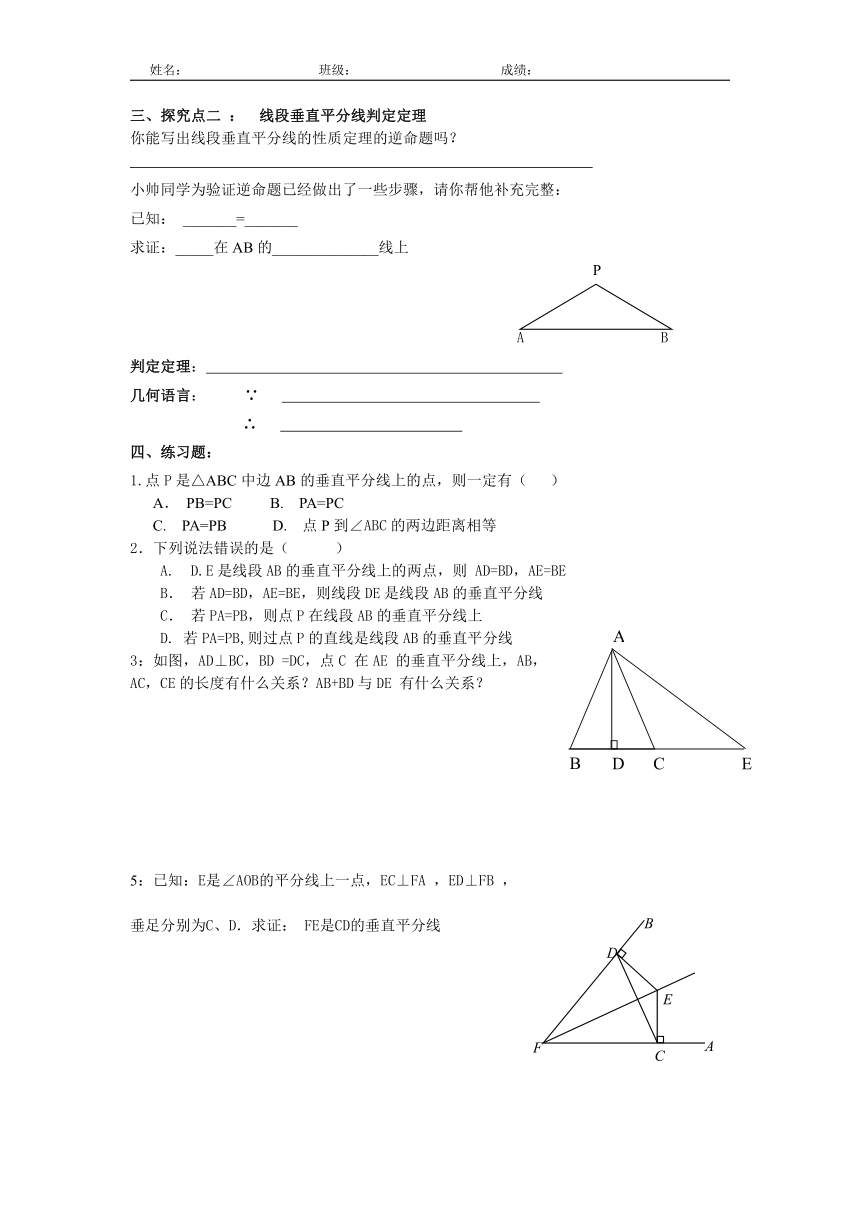
探究点一 : 线段垂直平分线性质定理
如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系并证明你的猜想
猜想:
已知: 直线l垂直平分_____,垂足为O,
点C在直线l上
求证:AC=________
证明:
线段垂直平分线性质定理:
几何语言: ∵
∴
跟踪训练: 如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗 为什么
三、探究点二 : 线段垂直平分线判定定理
你能写出线段垂直平分线的性质定理的逆命题吗?
小帅同学为验证逆命题已经做出了一些步骤,请你帮他补充完整:
已知: _______=_______
求证:_____在AB的______________线上
P
A B
判定定理:
几何语言: ∵
∴
四、练习题:
1.点P是△ABC中边AB的垂直平分线上的点,则一定有( )
A. PB=PC B. PA=PC
C. PA=PB D. 点P到∠ABC的两边距离相等
2.下列说法错误的是( )
A. D.E是线段AB的垂直平分线上的两点,则 AD=BD,AE=BE
B. 若AD=BD,AE=BE,则线段DE是线段AB的垂直平分线
C. 若PA=PB,则点P在线段AB的垂直平分线上
D. 若PA=PB,则过点P的直线是线段AB的垂直平分线
3:如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,
AC,CE的长度有什么关系?AB+BD与DE 有什么关系?
5:已知:E是∠AOB的平分线上一点,EC⊥FA ,ED⊥FB ,
垂足分别为C、D.求证: FE是CD的垂直平分线
13.1.2 线段垂直平分线(2)
复习巩固
1、如图所示,有A、B、C三个居民小区的位置成三角形,现决定在
三个小区之间修建一个购物超,使超市到三个小区的距离相等,
则超市应建在( )
A.在AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边垂直平分线的交点处
D.在A、B两内角平分线的交点处
2、作∠AOB的角平分线
A
O
B
预习课本P62---P63,完成下面的习题
问题导读:
如何作线段的垂直平分线?____________________________________
如何过直线外一点作这条直线的垂线?____________________________________
探究一:作已知直线的垂直平分线
已知:______________________
求作:_________________ A B
作法:_________________
探究二:过直线外一点作这条直线的垂线
已知:______________________ . P
求作:_____________________ A B
作法:______________________
跟踪训练:你能作出五角星的一条对称轴吗?
练一练:1、在直线l上找一点P到点A、点B距离相等,保留作图痕迹。
B·
A·
l
△ABC中,DE是AC的垂直平分线,垂足为E,交AB于点D,
AE=5cm,△CBD的周长为24cm,求△ABC的周长。
3.某地有两所大学和两条相交叉的公路,如图所示(点M,N表示大
学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所
大学的距离相等,到两条公路的距离也相等.
(1)你能确定仓库应该建在什么位置吗?在所给的图形中
画出你的设计方案;
(2)阐述你设计的理由.
4.如图,已知在△ABC中,AB=AC,∠BAC=120o,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
(提示:作AB的垂直平分线MN,交
AB、BC于分别于M、N,连接AF)
13.2 画轴对称图形(1)
一、知识链接:预习课本P62---P63,完成下面的习题
1、如图:你能做出它关于虚线的对称图形吗?
(1)找到点A的对称点A′
(2) A A′与对称轴有什么关系?
(3)在图中另找一对对称点,连接对称点的线段与对称轴还有上述关系吗?
归纳:连接任意一对对称点的线段被对称轴____________
二、预习自测:
如图,已知点A和直线l,试画出点C关于直线AB的对称点C′。
请说说你的画法 A
C·
B
三、探究点1:画已知图形的轴对称图形
作△ABC关于直线l的对称的图形△A′B′C′
画法:
跟踪训练:请画出三角形关于直线l对称的图形 1
A
C
B
四.探究点二:找对称轴
已知△ABC,及点A的对称点A′,请作出对称轴直线EF,并画出△ABC
关于直线EF的对称图形。
A . A′
B
C
练一练:
1.为学校运动会设计一徽标,要求贴近学生生活,突出运动主题,
要求是轴对称图案。
2、把下列图形补成关于对称的图形。新 课 标 第 一 网 ( http: / / www.xkb1.com / )
3、小明在平面镜中看到身后墙上钟表显示的时间是12:15,这时的实际时间应该是 。
4、为美化校园,学校准备在一块圆形空地上建花坛,现征集设计方案,要求设计的图案由圆、三角形、矩形组成(三种几何图案的个数不限),并且使整个圆形场地成轴对称图形,请你画出你的设计方案.
五.作业:请你完成<课堂作业>32到33页的练习
六、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
12.2 画轴对称图形(2)
一、知识链接::预习课本P62---P63,完成下面的习题
1、如图,在平面直角坐标系中,分别标出点A、B、C点的坐标。
二、探究点一:点关于x轴对称
(1)在坐标系中标出点A、B、C 关于x轴的对称点A1 、 B1、C1
(2)写出它们的坐标________________________________________________
(3)观察每对对称点的坐标,你发现了什么规律?
归纳:在平面直角坐标系中,关于x轴对称的点横坐标_____,,纵坐标_________________。点(x,y)关于x轴的对称点的坐标为__________.
跟踪训练:
点(3,6)、(-7,9)关于x轴的对称点分别是什么?
________________________________________________
三、探究点二:点关于y轴对称
(1)在坐标系中标出点A、B、C关于y轴的对称点A2、 B2、C2
(2)写出它们的坐标_____________________________________
(3)观察每对对称点的坐标,你发现了什么规律?
归纳:在平面直角坐标系中,关于y轴对称的点横坐标_____,纵坐标_________________。点(x,y)关于y轴的对称点的坐标为__________.
跟踪训练:
1、点(-3,-5)、(0,10)关于y轴的对称点分别是什么?
__________________________________________________________________________
2、完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
3、点(-1,3)与点(-1,—3)关于_________对称;
点(2,—4)与点(-2,—4)关于_________对称;
4、已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),
作出△ABC关于y轴对称的图形。
四、当堂检测
1.横坐标相同、纵坐标相反的两点,________________;
横坐标相反、纵坐标相同的两点,________________。
2、平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若与△ABC关于x轴对称,写出、、的坐标.
3、根据下列点的坐标,判断它们是关于X轴对称还是关于Y轴对称。
⑴ (-1,3)和(1,-3)关于______________对称
⑵ (-5,-4)和 (- 5,4)关于______________对称
⑶ (3,4)和 (-3,4)关于______________对称
⑷ (1,6)和(1,-6)关于_____________对称
4、点M (a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
5、已知点(x,4-y)与点(1-y,2x)关于y轴对称,则xy=_______。
6、已知A(-1,-2)和B(1,3),将点A向______平移________个单位长度后得到的点与点B关于y轴对称.
7、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
8.请完成《课堂作业》第33到34页的练习
9预习了本堂课,写一写你学到的知识,说在你的心得体会
13.3.1 等腰三角形(1)
预习自测:预习课本P75-P76,完成下面的习题
1、下列图形不一定是轴对称图形的是( )
A圆 B长方形 C线段D三角形
2、怎样的三角形是轴对称图形?答:
3、有两边相等的三角形叫 ,相等的两边叫 ,
另一边叫 两腰的夹角叫 ,腰和底边的夹角叫
4、如图,在△ABC中,AB=AC,
标出各部分名称
探究点一:等腰三角形的性质
1、探究:教材P75
把活动中剪出的△ABC沿折痕AD对折,找出其中重合的线段和角,
填入下表
(图1)
2、归纳等腰三角形的性质:
性质1 等腰三角形的两个 相等(简写成“ ” )
性质2 等腰三角形 、 、 互相重合。(简写成“ ” )
3、 根据图1 请你证明等腰三角形的性质1
跟踪训练:
1、(1)等腰三角形的一个角是110°,它的另外两个角的度数是
(2)等腰三角形的两条边分别是5cm、8cm,则它的周长是
2. 在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.
3 已知一个等腰三角形两个内角的度数之比为1:4,则这个等腰三角形顶角的度数为 。
4 等腰三角形一腰上的高和另一腰的夹角为40o,则底角为 。
5 如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
6如图,CA=CB,DF=DB,AE=AD
求∠A的度数
7如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证BD=CE
8、如图4,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为点M
求证:CM=DM
13.3.1 等腰三角形(2)
预习自测:预习课本P77—78页完成下面的练习题
1、等腰三角形的两边长分别为4,8,则周长为
2、等腰三角形的周长为14,其中一边长为6,则另两边分别为
3、等腰三角形的一个角为70°,则另外两个角的度数是
4、等腰三角形的一个角为120°则另外两个角的度数是
5、如图,在△ABC中,AB=AC,
(1)若AD平分∠BAC,那么 、
(2)若BD=CD,那么 、
(3)若AD⊥BC,那么 、
探究点一:等腰三角形的判定
1、思考:(1)如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当
测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点
(不考虑风浪因素)?
(2)我们把这个问题一般化,在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
已知:在△ABO中,∠A=∠B求证:AO=AO
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的 也相等(简写成 )
跟踪训练:
1、如图,AD∥BC,BD平分∠ABC. 求证:AB=AD.
2、如图,AC和BD相交于点O,且AB∥DC,OA=OB,
求证:OC=OD
3.如图,在△ABC中,AB=AC,∠B=36O,D、E是BC上的两点,
且∠ADE=∠AED=2∠BAD,则图中的等腰三角形共有( )个。
A.3个 B.4个 C.5个 D.6个
4、如图,∠A=∠B,CE∥DA,CE交AB于E,求证△CEB是等腰三角形
5求证:如果三角形一个外角的平分线平行于三角形的一边,那么这
个三角形是等腰三角形.
6、如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作
EF∥BC,交AB于点E,交AC于点F
求证:EF=EB+FC.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.证明
△OAE≌△OBE
13.3.2 等边三角形(1)
预习自测:预习课本P79到80页完成下面的练习
1、等腰三角形的性质:
(1)等腰三角形的 相等
(2)等腰三角形 、 、 互相重合
2、等腰三角形中有一种特殊的等腰三角形是 三角形,
即 叫等边三角形。
探究点一:等边三角形的性质
1、思考:(1)把等腰三角形的性质(等腰三角形的两个底角相等)用到
等边三角形,能得到什么结论?
2、归纳:(1)等边三角形的性质:等边三角形的
探究二:等边三角形的判定
1、思考:(1)一个三角形满足什么条件就是等边三角形?
(2)你认为有一个角等于60°的等腰三角形是等边三角形吗?
已知: A
求证:
证明:
B C
2、归纳
等边三角形的判定:
练一练:
1、如图,△ABC是等边三角形,DE∥BC,交AB,AC于D,E。
求证△ADE是等边三角形。
2、如图,D、E、F分别是等边△ABC各边上的点,且AD=BE=CF,
求证:△DEF是等边三角形
3如图,在等边中,点分别在边上,且,与交
于点.(1)求证:;(2)求的度数.
4、如图,是等边三角形内的一点,连结,以为边作,且,连结.证明=.
13.3.2 直角三角形
一、知识链接:预习课本P81页完成下面的练习题
1、等边三角形的性质:
2、等边三角形的判定:
二.探究点一:
问题:用两个全等的含30°角的直角三角尺,你能拼出一个怎样
的三角形?能拼出一个等边三角形吗?说说你的理由.
由1你能想到,在直角三角形中,30°角所对的直角边与斜边有
怎样的大小关系?你能用不同于课本上的方法证明你的结论吗?
已知:如图,在Rt△ABC中,∠C=90°,∠BAC=30°求证:BC=AB.
由2,我们得到下面的性质定理:
________________________________________________________
几何语言: ∵∠C=90o,∠A=30o
∴BC= ( )
跟踪训练:
点D是AB的中点, BC、DE垂直于AC垂足分别为C、E, AB=8m,∠A=30°,
求BC、DE各多长?
已知:如图,在△ABC中,AB=AC=2a,∠ABC=
∠ACB=15°,CD是腰AB上的高.求CD
2、已知:如图,△ABC中,∠ACB=90°,CD是高,∠A=30°.
AB=4 cm,求BD的长度
4. 例题:如图(5),要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植,
如果∠C=90°,∠A=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
5习了本堂课,写一写你学到的知识,说在你的心得体会
第十三章 轴对称复习练习题1.已知等腰三角形的一个角为42 0,则它的底角度数_______.
2.下列10个汉字:林 上 下 目 王 田 天 王 显 吕,其中不是轴对称图形的是_______;有一条对称轴的是________;有两条对称轴的是_______;有四条对称轴的是________.
3.如图,镜子中号码的实际号码是___________.
4.等腰三角形的两边长分别是和,则其周长为______.
5. 在平面直角坐标系中,点P(-2,1)关于 y轴对称的点的坐标为 .,点P(-2,1)关于 x轴对称的点的坐标为是 .
6.如图,AB=AC,,AB的垂直平分线交BC于点D,那么 。
7、如图,的周长为32,且于,的周长为24,那么的长为 .
8.如图,∠A=15°,AB=BC=CD=DE=EF,则∠FEM的度数为________.
9.如图,等腰三角形ABC中,AB=AC,一腰上的中线BD将这个等腰三角形周长分成15和6两部分,则这个三角形的腰长及底边长为________________________.
二、选择题1.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
2. 下列图形是轴对称图形的是( )
3.如图3,已知△ABC中,AC+BC=24,AO、BO分别是角平分线,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为( )
A.12 B.24 C.36 D.不确定
4.如图4所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中不一定相等的线段有( )
A.AC=AE=BE B.AD=BD C.CD=DE D.AC=BD
5.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A.30o B.40o C.45o D.36o
6.如图,等腰△ABC的周长为21,底边BC = 5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
A.13 B.14 C.15 D.16
7.如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )
A. B. C. D.
8、如图,在中, ,是的垂直平分线,交于点,交于点.已知,则的度数为( )
A. B. C. D.
三、解答题
1.如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是 .
2.如图,在方格纸上建立平面直角坐标系,线段AB的两个端点都在格点上,直线MN经过坐标原点。
(1)写出点A的坐标 , B的坐标 .
(2)利用尺规作出线段AB关于直线MN的对称图形(保留作图痕迹,不写作法)。
)。
4.如图,在等边中,点分别在边上,且,与交
于点.(1)求证:;(2)求的度数.
5.如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.
6. 如图所示,Rt△ABC中,∠C=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,求DE长。
7、如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,AF∥DC,连接AC、CF,求证:CA是∠DCF的平分线。
8.已知:如图所示,在和中,,,,且点在一条直线上,连接分别为的中点.
求证:①;②是等腰三角形.
9、如图,在⊿ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F,BE=5cm,CF=3cm,求EF的长.
10、已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
(1) 求证:AE=BE;
(2) 若∠AEC=45°,AC=1,求CE的长.
图
11、已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF, AF相交于P,M.(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
O
B
A
P3
P1
P2
l
C
B
A
C
D
E
D
E
C
B
A
F
E
D
C
B
A
N·
M·
B
O
A
B
C
A
A
重合的线段 重合的角
C
B
D
C
B
D
F
E
A
D
B
C
x
E
D
C
B
A
M
D
C
B
A
E
D
C
B
A
A
C
B
F
E
O
Q
C
P
A
B
A
B
C
A
图(5)
N
M
E
F
C
B
A
D
A
D
E
B C
A
B
M
C
N
O
图3
图4
A
C
B
D
E
A
C
B
D
E
C
E
N
D
A
B
M
O
A
B
E
C
F
13.1 轴对称学案(一)
(一)、预习课本P58---P60,完成下面的习题
(二)、概念:
(1)轴对称图形:如果一个图形沿一条 折叠,直线两旁的部分能够 ,这个图形就叫做 。这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线 。
(2)轴对称:把一个图形沿着某一条直线折叠,如果它能够与 重合,那么就说这两个图形关于这条直线成 。这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重叠的点)叫做 。
(3)轴对称图形和两个图形成轴对称有什么区别和联系?
区别: 轴对称是说 个图形的位置关系,
轴对称图形是说 个具有特殊形状的图形。
联系:都能沿着某条直线 。这条直线是对称轴。
(三)、思考:
(1)成轴对称的两个图形全等吗 全等的两个图形一定成轴对称吗?
(2)如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成 ;反过来,如果把两个成轴对称的图形看成一个整体,那么它就是一个 图形.
(四)、练一练:
1、标出下列图形中的对称点
2、下面给出的每幅图中的两个图案是轴对称的吗?如果是,试着找画它们的对称轴,并找出一对对称点.
3.等腰三角形的对称轴有( )
A、1条 B、3条 C、1条或3条 D、无数条
4.下列图形中不是轴对称图形的是( )
A B C D
5. 下列图案是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
6.下列英文字母属于轴对称图形的是( )
A、N B、S C、L D、E
7.下列各时刻是轴对称图形的为( )
A、 B、 C、 D、
8.如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是( ),折痕所在的直线叫做( )。
9.在对称图形中,对称轴两侧相对应的点到对称轴的( )。
10.( )三角形有三条对称轴,( )三角形有一条对称轴。
11.正方形有( )条对称轴,长方形有( )条对称轴,等腰梯形有( )条对称轴。
12.判断。
①.通过一个圆的圆心的直线是这个圆的对称轴。 ( )
②.圆是轴对称图形,每一条直径都是它的对称轴。( )
③.等腰梯形是对称图形。 ( )
④.正方形只有一条对称轴。 ( )
13.请写出下列图形的对称轴的条数
① 等边三角形 ② 正方形 ③ 圆
④ 长方形 ⑤平行四边形 ⑥正六边形
14.当写着数字的纸条垂直于镜面摆放时(如图所示):
下面是从镜子中看到的数: ,它实际上是________________
16.作图题,画下面图形的对称轴.
13.1.2线段垂直平分线性质定理
一、知识链接:
如图,四边形ABCD与四边形EFGH关于MN对称。
(1)A、B、C、D的对称点分别是 ,线段AD、AB的对应线段
分别是 ,CD= , ∠CBA= ,∠ADC=
(2)连接AE、BF,AE与BF平行吗?为什么?
(3)对称轴MN与线段AE的关系?
二、预习课本P61---P62,完成下面的习题
探究点一 : 线段垂直平分线性质定理
如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系并证明你的猜想
猜想:
已知: 直线l垂直平分_____,垂足为O,
点C在直线l上
求证:AC=________
证明:
线段垂直平分线性质定理:
几何语言: ∵
∴
跟踪训练: 如右图所示,直线MN和DE分别是线段 AB、BC的垂直平分线,它们交于P点,请问PA和 PC相等吗 为什么
三、探究点二 : 线段垂直平分线判定定理
你能写出线段垂直平分线的性质定理的逆命题吗?
小帅同学为验证逆命题已经做出了一些步骤,请你帮他补充完整:
已知: _______=_______
求证:_____在AB的______________线上
P
A B
判定定理:
几何语言: ∵
∴
四、练习题:
1.点P是△ABC中边AB的垂直平分线上的点,则一定有( )
A. PB=PC B. PA=PC
C. PA=PB D. 点P到∠ABC的两边距离相等
2.下列说法错误的是( )
A. D.E是线段AB的垂直平分线上的两点,则 AD=BD,AE=BE
B. 若AD=BD,AE=BE,则线段DE是线段AB的垂直平分线
C. 若PA=PB,则点P在线段AB的垂直平分线上
D. 若PA=PB,则过点P的直线是线段AB的垂直平分线
3:如图,AD⊥BC,BD =DC,点C 在AE 的垂直平分线上,AB,
AC,CE的长度有什么关系?AB+BD与DE 有什么关系?
5:已知:E是∠AOB的平分线上一点,EC⊥FA ,ED⊥FB ,
垂足分别为C、D.求证: FE是CD的垂直平分线
13.1.2 线段垂直平分线(2)
复习巩固
1、如图所示,有A、B、C三个居民小区的位置成三角形,现决定在
三个小区之间修建一个购物超,使超市到三个小区的距离相等,
则超市应建在( )
A.在AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边垂直平分线的交点处
D.在A、B两内角平分线的交点处
2、作∠AOB的角平分线
A
O
B
预习课本P62---P63,完成下面的习题
问题导读:
如何作线段的垂直平分线?____________________________________
如何过直线外一点作这条直线的垂线?____________________________________
探究一:作已知直线的垂直平分线
已知:______________________
求作:_________________ A B
作法:_________________
探究二:过直线外一点作这条直线的垂线
已知:______________________ . P
求作:_____________________ A B
作法:______________________
跟踪训练:你能作出五角星的一条对称轴吗?
练一练:1、在直线l上找一点P到点A、点B距离相等,保留作图痕迹。
B·
A·
l
△ABC中,DE是AC的垂直平分线,垂足为E,交AB于点D,
AE=5cm,△CBD的周长为24cm,求△ABC的周长。
3.某地有两所大学和两条相交叉的公路,如图所示(点M,N表示大
学,AO,BO表示公路).现计划修建一座物资仓库,希望仓库到两所
大学的距离相等,到两条公路的距离也相等.
(1)你能确定仓库应该建在什么位置吗?在所给的图形中
画出你的设计方案;
(2)阐述你设计的理由.
4.如图,已知在△ABC中,AB=AC,∠BAC=120o,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.
(提示:作AB的垂直平分线MN,交
AB、BC于分别于M、N,连接AF)
13.2 画轴对称图形(1)
一、知识链接:预习课本P62---P63,完成下面的习题
1、如图:你能做出它关于虚线的对称图形吗?
(1)找到点A的对称点A′
(2) A A′与对称轴有什么关系?
(3)在图中另找一对对称点,连接对称点的线段与对称轴还有上述关系吗?
归纳:连接任意一对对称点的线段被对称轴____________
二、预习自测:
如图,已知点A和直线l,试画出点C关于直线AB的对称点C′。
请说说你的画法 A
C·
B
三、探究点1:画已知图形的轴对称图形
作△ABC关于直线l的对称的图形△A′B′C′
画法:
跟踪训练:请画出三角形关于直线l对称的图形 1
A
C
B
四.探究点二:找对称轴
已知△ABC,及点A的对称点A′,请作出对称轴直线EF,并画出△ABC
关于直线EF的对称图形。
A . A′
B
C
练一练:
1.为学校运动会设计一徽标,要求贴近学生生活,突出运动主题,
要求是轴对称图案。
2、把下列图形补成关于对称的图形。新 课 标 第 一 网 ( http: / / www.xkb1.com / )
3、小明在平面镜中看到身后墙上钟表显示的时间是12:15,这时的实际时间应该是 。
4、为美化校园,学校准备在一块圆形空地上建花坛,现征集设计方案,要求设计的图案由圆、三角形、矩形组成(三种几何图案的个数不限),并且使整个圆形场地成轴对称图形,请你画出你的设计方案.
五.作业:请你完成<课堂作业>32到33页的练习
六、学习反思
请你对照学习目标,谈一下这节课的收获及困惑。
12.2 画轴对称图形(2)
一、知识链接::预习课本P62---P63,完成下面的习题
1、如图,在平面直角坐标系中,分别标出点A、B、C点的坐标。
二、探究点一:点关于x轴对称
(1)在坐标系中标出点A、B、C 关于x轴的对称点A1 、 B1、C1
(2)写出它们的坐标________________________________________________
(3)观察每对对称点的坐标,你发现了什么规律?
归纳:在平面直角坐标系中,关于x轴对称的点横坐标_____,,纵坐标_________________。点(x,y)关于x轴的对称点的坐标为__________.
跟踪训练:
点(3,6)、(-7,9)关于x轴的对称点分别是什么?
________________________________________________
三、探究点二:点关于y轴对称
(1)在坐标系中标出点A、B、C关于y轴的对称点A2、 B2、C2
(2)写出它们的坐标_____________________________________
(3)观察每对对称点的坐标,你发现了什么规律?
归纳:在平面直角坐标系中,关于y轴对称的点横坐标_____,纵坐标_________________。点(x,y)关于y轴的对称点的坐标为__________.
跟踪训练:
1、点(-3,-5)、(0,10)关于y轴的对称点分别是什么?
__________________________________________________________________________
2、完成下表.
已知点 (2,-3) (-1,2) (-6,-5) (0,-1.6) (4,0)
关于x轴的对称点
关于y轴的对称点
3、点(-1,3)与点(-1,—3)关于_________对称;
点(2,—4)与点(-2,—4)关于_________对称;
4、已知△ABC的三个顶点的坐标分别为A(-3,5),B(- 4,1),C(-1,3),
作出△ABC关于y轴对称的图形。
四、当堂检测
1.横坐标相同、纵坐标相反的两点,________________;
横坐标相反、纵坐标相同的两点,________________。
2、平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若与△ABC关于x轴对称,写出、、的坐标.
3、根据下列点的坐标,判断它们是关于X轴对称还是关于Y轴对称。
⑴ (-1,3)和(1,-3)关于______________对称
⑵ (-5,-4)和 (- 5,4)关于______________对称
⑶ (3,4)和 (-3,4)关于______________对称
⑷ (1,6)和(1,-6)关于_____________对称
4、点M (a, -5)与点N(-2, b)关于y轴对称,则a=_____, b =_____.
5、已知点(x,4-y)与点(1-y,2x)关于y轴对称,则xy=_______。
6、已知A(-1,-2)和B(1,3),将点A向______平移________个单位长度后得到的点与点B关于y轴对称.
7、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
8.请完成《课堂作业》第33到34页的练习
9预习了本堂课,写一写你学到的知识,说在你的心得体会
13.3.1 等腰三角形(1)
预习自测:预习课本P75-P76,完成下面的习题
1、下列图形不一定是轴对称图形的是( )
A圆 B长方形 C线段D三角形
2、怎样的三角形是轴对称图形?答:
3、有两边相等的三角形叫 ,相等的两边叫 ,
另一边叫 两腰的夹角叫 ,腰和底边的夹角叫
4、如图,在△ABC中,AB=AC,
标出各部分名称
探究点一:等腰三角形的性质
1、探究:教材P75
把活动中剪出的△ABC沿折痕AD对折,找出其中重合的线段和角,
填入下表
(图1)
2、归纳等腰三角形的性质:
性质1 等腰三角形的两个 相等(简写成“ ” )
性质2 等腰三角形 、 、 互相重合。(简写成“ ” )
3、 根据图1 请你证明等腰三角形的性质1
跟踪训练:
1、(1)等腰三角形的一个角是110°,它的另外两个角的度数是
(2)等腰三角形的两条边分别是5cm、8cm,则它的周长是
2. 在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,
求△ABC各角的度数.
3 已知一个等腰三角形两个内角的度数之比为1:4,则这个等腰三角形顶角的度数为 。
4 等腰三角形一腰上的高和另一腰的夹角为40o,则底角为 。
5 如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
6如图,CA=CB,DF=DB,AE=AD
求∠A的度数
7如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证BD=CE
8、如图4,AB=AE,BC=DE,∠B=∠E,AM⊥CD,垂足为点M
求证:CM=DM
13.3.1 等腰三角形(2)
预习自测:预习课本P77—78页完成下面的练习题
1、等腰三角形的两边长分别为4,8,则周长为
2、等腰三角形的周长为14,其中一边长为6,则另两边分别为
3、等腰三角形的一个角为70°,则另外两个角的度数是
4、等腰三角形的一个角为120°则另外两个角的度数是
5、如图,在△ABC中,AB=AC,
(1)若AD平分∠BAC,那么 、
(2)若BD=CD,那么 、
(3)若AD⊥BC,那么 、
探究点一:等腰三角形的判定
1、思考:(1)如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当
测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点
(不考虑风浪因素)?
(2)我们把这个问题一般化,在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
已知:在△ABO中,∠A=∠B求证:AO=AO
等腰三角形的判定方法:
如果一个三角形有两个角相等,那么这两个角所对的 也相等(简写成 )
跟踪训练:
1、如图,AD∥BC,BD平分∠ABC. 求证:AB=AD.
2、如图,AC和BD相交于点O,且AB∥DC,OA=OB,
求证:OC=OD
3.如图,在△ABC中,AB=AC,∠B=36O,D、E是BC上的两点,
且∠ADE=∠AED=2∠BAD,则图中的等腰三角形共有( )个。
A.3个 B.4个 C.5个 D.6个
4、如图,∠A=∠B,CE∥DA,CE交AB于E,求证△CEB是等腰三角形
5求证:如果三角形一个外角的平分线平行于三角形的一边,那么这
个三角形是等腰三角形.
6、如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作
EF∥BC,交AB于点E,交AC于点F
求证:EF=EB+FC.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.证明
△OAE≌△OBE
13.3.2 等边三角形(1)
预习自测:预习课本P79到80页完成下面的练习
1、等腰三角形的性质:
(1)等腰三角形的 相等
(2)等腰三角形 、 、 互相重合
2、等腰三角形中有一种特殊的等腰三角形是 三角形,
即 叫等边三角形。
探究点一:等边三角形的性质
1、思考:(1)把等腰三角形的性质(等腰三角形的两个底角相等)用到
等边三角形,能得到什么结论?
2、归纳:(1)等边三角形的性质:等边三角形的
探究二:等边三角形的判定
1、思考:(1)一个三角形满足什么条件就是等边三角形?
(2)你认为有一个角等于60°的等腰三角形是等边三角形吗?
已知: A
求证:
证明:
B C
2、归纳
等边三角形的判定:
练一练:
1、如图,△ABC是等边三角形,DE∥BC,交AB,AC于D,E。
求证△ADE是等边三角形。
2、如图,D、E、F分别是等边△ABC各边上的点,且AD=BE=CF,
求证:△DEF是等边三角形
3如图,在等边中,点分别在边上,且,与交
于点.(1)求证:;(2)求的度数.
4、如图,是等边三角形内的一点,连结,以为边作,且,连结.证明=.
13.3.2 直角三角形
一、知识链接:预习课本P81页完成下面的练习题
1、等边三角形的性质:
2、等边三角形的判定:
二.探究点一:
问题:用两个全等的含30°角的直角三角尺,你能拼出一个怎样
的三角形?能拼出一个等边三角形吗?说说你的理由.
由1你能想到,在直角三角形中,30°角所对的直角边与斜边有
怎样的大小关系?你能用不同于课本上的方法证明你的结论吗?
已知:如图,在Rt△ABC中,∠C=90°,∠BAC=30°求证:BC=AB.
由2,我们得到下面的性质定理:
________________________________________________________
几何语言: ∵∠C=90o,∠A=30o
∴BC= ( )
跟踪训练:
点D是AB的中点, BC、DE垂直于AC垂足分别为C、E, AB=8m,∠A=30°,
求BC、DE各多长?
已知:如图,在△ABC中,AB=AC=2a,∠ABC=
∠ACB=15°,CD是腰AB上的高.求CD
2、已知:如图,△ABC中,∠ACB=90°,CD是高,∠A=30°.
AB=4 cm,求BD的长度
4. 例题:如图(5),要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植,
如果∠C=90°,∠A=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
5习了本堂课,写一写你学到的知识,说在你的心得体会
第十三章 轴对称复习练习题1.已知等腰三角形的一个角为42 0,则它的底角度数_______.
2.下列10个汉字:林 上 下 目 王 田 天 王 显 吕,其中不是轴对称图形的是_______;有一条对称轴的是________;有两条对称轴的是_______;有四条对称轴的是________.
3.如图,镜子中号码的实际号码是___________.
4.等腰三角形的两边长分别是和,则其周长为______.
5. 在平面直角坐标系中,点P(-2,1)关于 y轴对称的点的坐标为 .,点P(-2,1)关于 x轴对称的点的坐标为是 .
6.如图,AB=AC,,AB的垂直平分线交BC于点D,那么 。
7、如图,的周长为32,且于,的周长为24,那么的长为 .
8.如图,∠A=15°,AB=BC=CD=DE=EF,则∠FEM的度数为________.
9.如图,等腰三角形ABC中,AB=AC,一腰上的中线BD将这个等腰三角形周长分成15和6两部分,则这个三角形的腰长及底边长为________________________.
二、选择题1.到三角形三条边的距离都相等的点是这个三角形的( )
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
2. 下列图形是轴对称图形的是( )
3.如图3,已知△ABC中,AC+BC=24,AO、BO分别是角平分线,且MN∥BA,分别交AC于N、BC于M,则△CMN的周长为( )
A.12 B.24 C.36 D.不确定
4.如图4所示,Rt△ABC中,∠C=90°,AB的垂直平分线DE交BC于D,交AB于点E.当∠B=30°时,图中不一定相等的线段有( )
A.AC=AE=BE B.AD=BD C.CD=DE D.AC=BD
5.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A.30o B.40o C.45o D.36o
6.如图,等腰△ABC的周长为21,底边BC = 5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
A.13 B.14 C.15 D.16
7.如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )
A. B. C. D.
8、如图,在中, ,是的垂直平分线,交于点,交于点.已知,则的度数为( )
A. B. C. D.
三、解答题
1.如图所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是 .
2.如图,在方格纸上建立平面直角坐标系,线段AB的两个端点都在格点上,直线MN经过坐标原点。
(1)写出点A的坐标 , B的坐标 .
(2)利用尺规作出线段AB关于直线MN的对称图形(保留作图痕迹,不写作法)。
)。
4.如图,在等边中,点分别在边上,且,与交
于点.(1)求证:;(2)求的度数.
5.如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.
6. 如图所示,Rt△ABC中,∠C=90°,∠A=30°,AB=8,CD是斜边AB上的高,CE是中线,求DE长。
7、如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,AF∥DC,连接AC、CF,求证:CA是∠DCF的平分线。
8.已知:如图所示,在和中,,,,且点在一条直线上,连接分别为的中点.
求证:①;②是等腰三角形.
9、如图,在⊿ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F,BE=5cm,CF=3cm,求EF的长.
10、已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
(1) 求证:AE=BE;
(2) 若∠AEC=45°,AC=1,求CE的长.
图
11、已知:如图, AF平分∠BAC,BC⊥AF, 垂足为E,点D与点A关于点E对称,PB分别与线段CF, AF相交于P,M.(1)求证:AB=CD;
(2)若∠BAC=2∠MPC,请你判断∠F与∠MCD的数量关系,并说明理由.
O
B
A
P3
P1
P2
l
C
B
A
C
D
E
D
E
C
B
A
F
E
D
C
B
A
N·
M·
B
O
A
B
C
A
A
重合的线段 重合的角
C
B
D
C
B
D
F
E
A
D
B
C
x
E
D
C
B
A
M
D
C
B
A
E
D
C
B
A
A
C
B
F
E
O
Q
C
P
A
B
A
B
C
A
图(5)
N
M
E
F
C
B
A
D
A
D
E
B C
A
B
M
C
N
O
图3
图4
A
C
B
D
E
A
C
B
D
E
C
E
N
D
A
B
M
O
A
B
E
C
F
