《志鸿全优设计》2013-2014学年高中数学人教A选修1-2单元目标检测:第二章 推理与证明(含解析)
文档属性
| 名称 | 《志鸿全优设计》2013-2014学年高中数学人教A选修1-2单元目标检测:第二章 推理与证明(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-10 13:55:43 | ||
图片预览

文档简介
数学人教A选修1-2第二章 推理与证明单元检测
(时间:45分钟,满分:100分)
一、选择题(每小题6分,共48分)
1.若有一段演绎推理:“大前提:对任意实数a,都有.小前提:已知a=-2为实数.结论:.”这个结论显然错误,是因为( ).
A.大前提错误 B.小前提错误
C.推理形式错误 D.非以上错误
2.用反证法证明命题“若a2+b2=0,则a,b全为0(a,bR)”,其反设正确的是( ).
A.a,b至少有一个不为0
B.a,b至少有一个为0
C.a,b全部为0
D.a,b中只有一个为0
3.观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为( ).
A.76 B.80
C.86 D.92[来源:.Com]
4.分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证”索的因应是( ).
A.a-b>0
B.a-c<0
C.(a-b)(a-c)>0
D.(a-b)(a-c)<0
5.已知点A(x1,),B(x2,)是函数y=x2图象上任意不同的两点,依据图象知,线段AB总是位于A,B两点之间函数图象的上方,因此有结论成立,运用类比方法可知,若点A(x1,sinx1),B(x2,sinx2)是函数y=sinx(x(0,π))图象上不同的两点,则类似地有结论( ).
A.
B.
C.
D.
6.要证a2+b2-1-a2b2≤0,只要证明( ).
A.2ab-1-a2b2≤0
B.a2+b2-1-≤0
C.-1-a2b2≤0
D.(a2-1)(b2-1)≥0
7.若,(a≥0),则P,Q的大小关系是( ).
A.P>Q B.P=Q
C.P<Q D.由a的取值确定
∵0<12成立,∴P<Q成立.
8.命题:“若空间两条直线a,b分别垂直于平面α,则a∥b.”学生小夏这样证明:设a,b与面α分别相交于A,B,连接A,B.
∵a⊥α,b⊥α,ABα,①
∴a⊥AB,b⊥AB,②
∴a∥b.③
这里的证明有两个推理,p:①②,q:②③,则下列命题为真命题的是( ).
A.p∧q B.p∨q
C.p∨q D.(p)∧(q)
二、填空题(每小题6分,共18分)[来源:学#科#网]
9.把“函数y=x2-x+1的图象是一条抛物线”恢复成三段论的形式:
大前提:___________________________________________________________________;
小前提:____________________________________________________________________;
结论:_____________________________________________________________________.
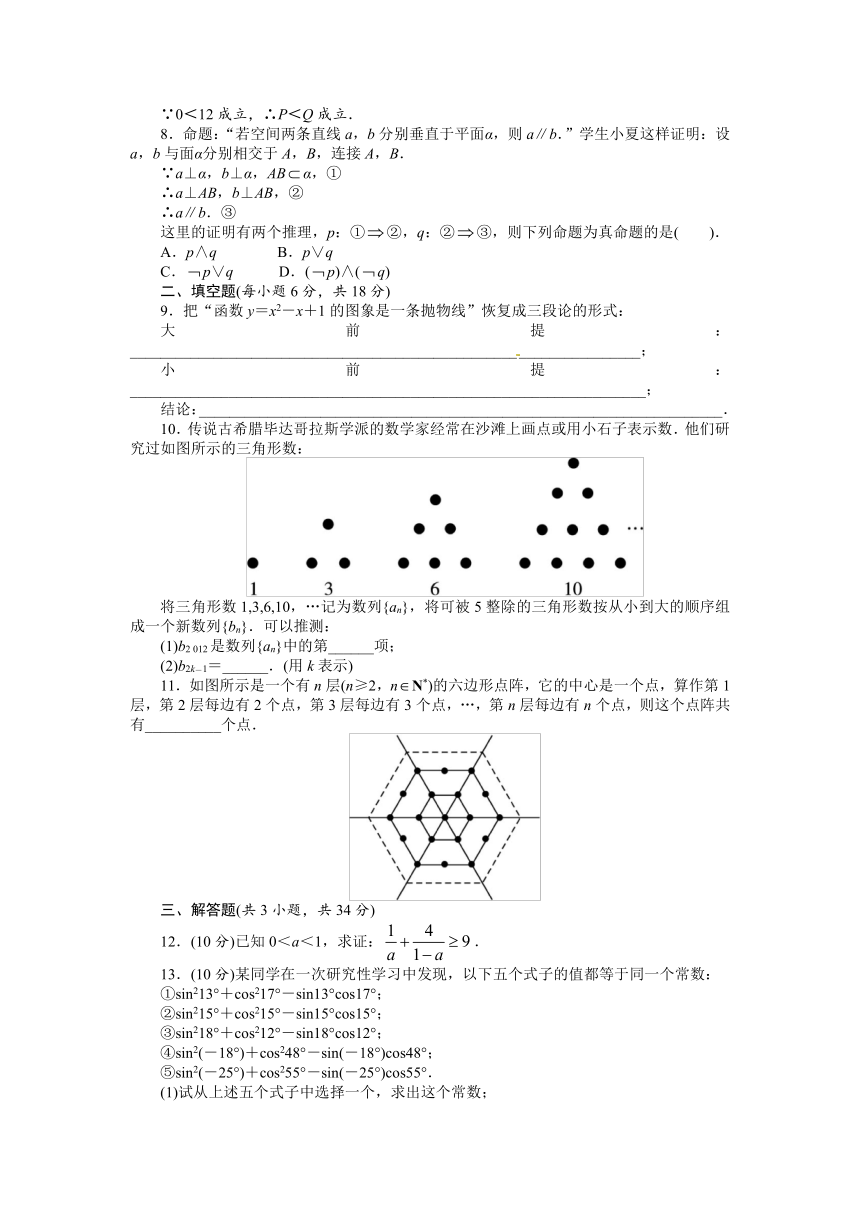
10.传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图所示的三角形数:
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}.可以推测:
(1)b2 012是数列{an}中的第______项;
(2)b2k-1=______.(用k表示)
11.如图所示是一个有n层(n≥2,nN*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有__________个点.
三、解答题(共3小题,共34分)
12.(10分)已知0<a<1,求证:.
13.(10分)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°-sin13°cos17°;
②sin215°+cos215°-sin15°cos15°;
③sin218°+cos212°-sin18°cos12°;
④sin2(-18°)+cos248°-sin(-18°)cos48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos55°.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
14.(14分)如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,运用三段论证明BD⊥平面PAC.
参考答案
1答案:A 解析:当n为偶数时,若有意义,则a≥0,故大前提错误.
2答案:A 解析:a,b全为0的反面是a,b至少有一个不为0,故选A.
3答案:B 解析:由已知条件得,|x|+|y|=n(nN+)的不同整数解(x,y)的个数为4n,所以|x|+|y|=20的不同整数解(x,y)的个数为80,故选B.
4答案:C 解析:欲证,即证b2-ac<3a2.
∵a+b+c=0,∴b=-(a+c).
只需证(a+c)2-ac<3a2,即证2a2-c2-ac>0,即证a2-c2+a2-ac>0,即证(a+c)(a-c)+a(a-c)>0,即证(a-c)[(a+c)+a]>0.
又b=-(a+c),即证(a-c)(a-b)>0,故选C.
5答案:B 解析:画出y=x2的图象,由已知得AB的中点恒在点的上方,画出y=sinx,x(0,π)的图象可得A,B的中点恒在点的下方,故B正确.
6答案:D 解析:因为a2+b2-1-a2b2≤0(a2-1)(b2-1)≥0.[来源:学科网]
7答案:C 解析:假设P<Q,∵要证P<Q,只要证P2<Q2,
只要证:2a+7+<2a+7+,
只要证:a2+7a<a2+7a+12,
只要证:0<12,
8答案:B 解析:易知p为真,q为假,则p∨q为真.
9答案:二次函数的图象是一条抛物线 y=x2-x+1是二次函数 y=x2-x+1的图象是一条抛物线
10答案:5 030 (2) 解析:(1)由题意可得,a1=1,a2=3,a3=6,a4=10,…,a2-a1=2,a3-a2=3,a4-a3=4,…,an-an-1=n.
以上各式相加得,an-a1=2+3+…+n=,故an=.因此,b1=a4=10,b2=a5=15,b3=a9=45,b4=a10=55,…
由此归纳出b2 012=a5 030.[来源:学&科&网]
答案:b1=a4=,b3=a9=,b5=a14=,….
归纳出.
11答案:3n2-3n+1 解析:设第n层共有an个点,结合图形可知a1=1,a2=6,…,an+1=an+6(n≥2,nN*),
则an=6+(n-2)×6=6n-6(n≥2,nN*),前n层所有点数之和为Sn=1+=3n2-3n+1,
故这个点阵共有3n2-3n+1个点.[来源:.Com]
12答案:证明:由于0<a<1,∴1-a>0.
要证明≥9,
只需证明1-a+4a≥9a-9a2,即9a2-6a+1≥0.
只需证明(3a-1)2≥0,
∵(3a-1)2≥0显然成立,∴原不等式成立.
13答案:
解法一:(1)选择②式,计算如下:
sin215°+cos215°-sin15°cos 15°==1-=.
(2)三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)=.
证明如下:
sin2α+cos2(30°-α)-sinαcos(30°-α)
=sin2α+(cos 30°cos α+sin30°sinα)2-sinα(cos 30°cos α+sin30°sinα)
=
=.
解法二:(1)同解法一.
(2)三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)=.
证明如下:
sin2α+cos2(30°-α)-sinαcos(30°-α)
=-sinα(cos30°cosα+sin30°sinα)
=(cos60°cos2α+sin60°sin2α)-
=
=.
14答案:
证明:∵一条直线与一个平面垂直,那么这条直线垂直于这个平面内的所有直线,大前提
∵PO⊥平面ABCD,BD平面ABCD,………………………………………小前提
∴PO⊥BD.…………………………………………………………………………结论
又正方形的对角线相互垂直,……………………………………………………大前提
AC,BD分别为正方形ABCD的两条对角线,……………………………………小前提
∴BD⊥AC.…………………………………………………………………………结论
又∵如果一条直线垂直于同一平面内的两条相交直线,则这条直线与该平面垂直,……大前提
BD⊥PO,BD⊥AC,POAC=O,……………………………………………………小前提
∴BD⊥平面PAC.…………………………………………………………………………结论
(时间:45分钟,满分:100分)
一、选择题(每小题6分,共48分)
1.若有一段演绎推理:“大前提:对任意实数a,都有.小前提:已知a=-2为实数.结论:.”这个结论显然错误,是因为( ).
A.大前提错误 B.小前提错误
C.推理形式错误 D.非以上错误
2.用反证法证明命题“若a2+b2=0,则a,b全为0(a,bR)”,其反设正确的是( ).
A.a,b至少有一个不为0
B.a,b至少有一个为0
C.a,b全部为0
D.a,b中只有一个为0
3.观察下列事实:|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12,…,则|x|+|y|=20的不同整数解(x,y)的个数为( ).
A.76 B.80
C.86 D.92[来源:.Com]
4.分析法又称执果索因法,若用分析法证明:“设a>b>c,且a+b+c=0,求证”索的因应是( ).
A.a-b>0
B.a-c<0
C.(a-b)(a-c)>0
D.(a-b)(a-c)<0
5.已知点A(x1,),B(x2,)是函数y=x2图象上任意不同的两点,依据图象知,线段AB总是位于A,B两点之间函数图象的上方,因此有结论成立,运用类比方法可知,若点A(x1,sinx1),B(x2,sinx2)是函数y=sinx(x(0,π))图象上不同的两点,则类似地有结论( ).
A.
B.
C.
D.
6.要证a2+b2-1-a2b2≤0,只要证明( ).
A.2ab-1-a2b2≤0
B.a2+b2-1-≤0
C.-1-a2b2≤0
D.(a2-1)(b2-1)≥0
7.若,(a≥0),则P,Q的大小关系是( ).
A.P>Q B.P=Q
C.P<Q D.由a的取值确定
∵0<12成立,∴P<Q成立.
8.命题:“若空间两条直线a,b分别垂直于平面α,则a∥b.”学生小夏这样证明:设a,b与面α分别相交于A,B,连接A,B.
∵a⊥α,b⊥α,ABα,①
∴a⊥AB,b⊥AB,②
∴a∥b.③
这里的证明有两个推理,p:①②,q:②③,则下列命题为真命题的是( ).
A.p∧q B.p∨q
C.p∨q D.(p)∧(q)
二、填空题(每小题6分,共18分)[来源:学#科#网]
9.把“函数y=x2-x+1的图象是一条抛物线”恢复成三段论的形式:
大前提:___________________________________________________________________;
小前提:____________________________________________________________________;
结论:_____________________________________________________________________.
10.传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图所示的三角形数:
将三角形数1,3,6,10,…记为数列{an},将可被5整除的三角形数按从小到大的顺序组成一个新数列{bn}.可以推测:
(1)b2 012是数列{an}中的第______项;
(2)b2k-1=______.(用k表示)
11.如图所示是一个有n层(n≥2,nN*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有__________个点.
三、解答题(共3小题,共34分)
12.(10分)已知0<a<1,求证:.
13.(10分)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°-sin13°cos17°;
②sin215°+cos215°-sin15°cos15°;
③sin218°+cos212°-sin18°cos12°;
④sin2(-18°)+cos248°-sin(-18°)cos48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos55°.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
14.(14分)如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,运用三段论证明BD⊥平面PAC.
参考答案
1答案:A 解析:当n为偶数时,若有意义,则a≥0,故大前提错误.
2答案:A 解析:a,b全为0的反面是a,b至少有一个不为0,故选A.
3答案:B 解析:由已知条件得,|x|+|y|=n(nN+)的不同整数解(x,y)的个数为4n,所以|x|+|y|=20的不同整数解(x,y)的个数为80,故选B.
4答案:C 解析:欲证,即证b2-ac<3a2.
∵a+b+c=0,∴b=-(a+c).
只需证(a+c)2-ac<3a2,即证2a2-c2-ac>0,即证a2-c2+a2-ac>0,即证(a+c)(a-c)+a(a-c)>0,即证(a-c)[(a+c)+a]>0.
又b=-(a+c),即证(a-c)(a-b)>0,故选C.
5答案:B 解析:画出y=x2的图象,由已知得AB的中点恒在点的上方,画出y=sinx,x(0,π)的图象可得A,B的中点恒在点的下方,故B正确.
6答案:D 解析:因为a2+b2-1-a2b2≤0(a2-1)(b2-1)≥0.[来源:学科网]
7答案:C 解析:假设P<Q,∵要证P<Q,只要证P2<Q2,
只要证:2a+7+<2a+7+,
只要证:a2+7a<a2+7a+12,
只要证:0<12,
8答案:B 解析:易知p为真,q为假,则p∨q为真.
9答案:二次函数的图象是一条抛物线 y=x2-x+1是二次函数 y=x2-x+1的图象是一条抛物线
10答案:5 030 (2) 解析:(1)由题意可得,a1=1,a2=3,a3=6,a4=10,…,a2-a1=2,a3-a2=3,a4-a3=4,…,an-an-1=n.
以上各式相加得,an-a1=2+3+…+n=,故an=.因此,b1=a4=10,b2=a5=15,b3=a9=45,b4=a10=55,…
由此归纳出b2 012=a5 030.[来源:学&科&网]
答案:b1=a4=,b3=a9=,b5=a14=,….
归纳出.
11答案:3n2-3n+1 解析:设第n层共有an个点,结合图形可知a1=1,a2=6,…,an+1=an+6(n≥2,nN*),
则an=6+(n-2)×6=6n-6(n≥2,nN*),前n层所有点数之和为Sn=1+=3n2-3n+1,
故这个点阵共有3n2-3n+1个点.[来源:.Com]
12答案:证明:由于0<a<1,∴1-a>0.
要证明≥9,
只需证明1-a+4a≥9a-9a2,即9a2-6a+1≥0.
只需证明(3a-1)2≥0,
∵(3a-1)2≥0显然成立,∴原不等式成立.
13答案:
解法一:(1)选择②式,计算如下:
sin215°+cos215°-sin15°cos 15°==1-=.
(2)三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)=.
证明如下:
sin2α+cos2(30°-α)-sinαcos(30°-α)
=sin2α+(cos 30°cos α+sin30°sinα)2-sinα(cos 30°cos α+sin30°sinα)
=
=.
解法二:(1)同解法一.
(2)三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)=.
证明如下:
sin2α+cos2(30°-α)-sinαcos(30°-α)
=-sinα(cos30°cosα+sin30°sinα)
=(cos60°cos2α+sin60°sin2α)-
=
=.
14答案:
证明:∵一条直线与一个平面垂直,那么这条直线垂直于这个平面内的所有直线,大前提
∵PO⊥平面ABCD,BD平面ABCD,………………………………………小前提
∴PO⊥BD.…………………………………………………………………………结论
又正方形的对角线相互垂直,……………………………………………………大前提
AC,BD分别为正方形ABCD的两条对角线,……………………………………小前提
∴BD⊥AC.…………………………………………………………………………结论
又∵如果一条直线垂直于同一平面内的两条相交直线,则这条直线与该平面垂直,……大前提
BD⊥PO,BD⊥AC,POAC=O,……………………………………………………小前提
∴BD⊥平面PAC.…………………………………………………………………………结论
