《志鸿全优设计》2013-2014学年高中数学人教A选修2-1单元目标检测:第三章 空间向量与立体几何(含解析)
文档属性
| 名称 | 《志鸿全优设计》2013-2014学年高中数学人教A选修2-1单元目标检测:第三章 空间向量与立体几何(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-10 00:00:00 | ||
图片预览


文档简介
数学人教A选修2-1第三章 空间向量与立体几何单元检测
(时间:45分钟,满分:100分)
一、选择题(每小题6分,共48分)
1.已知点A(-4,8,6),则点A关于y轴对称的点的坐标为( ).
A.(-4,-8,6) B.(-4,-8,-6)
C.(-6,-8,4) D.(4,8,-6)
2.若a=(0,1,-1),b=(1,1,0),且(a+λb)⊥a,则实数λ的值为( ).
A.-1 B.0 C.1 D.-2
3.若向量a=(1,λ,2),b=(2,-1,2),a,b夹角的余弦值为,则λ等于( ),
A.2 B.-2
C.-2或 D.2或
4.已知a=(2,-1,2),b=(2,2,1),则以a,b为邻边的平行四边形的面积为( ).
A. B. C.4 D.8
5.如图,在四面体ABCD中,已知=b,=a,=c,,则等于( ).
A.
B.
C.
D.
6.在三棱锥P-ABC中,△ABC为等边三角形,PA⊥平面ABC,且PA=AB,则二面角A-PB-C的平面角的正切值为( ).
A. B. C. D.
7.已知A(1,2,3),B(2,1,2),P(1,1,2),点Q在直线OP上运动(O为原点),则当取最小值时,点Q的坐标为( ).
A. B.
C. D.
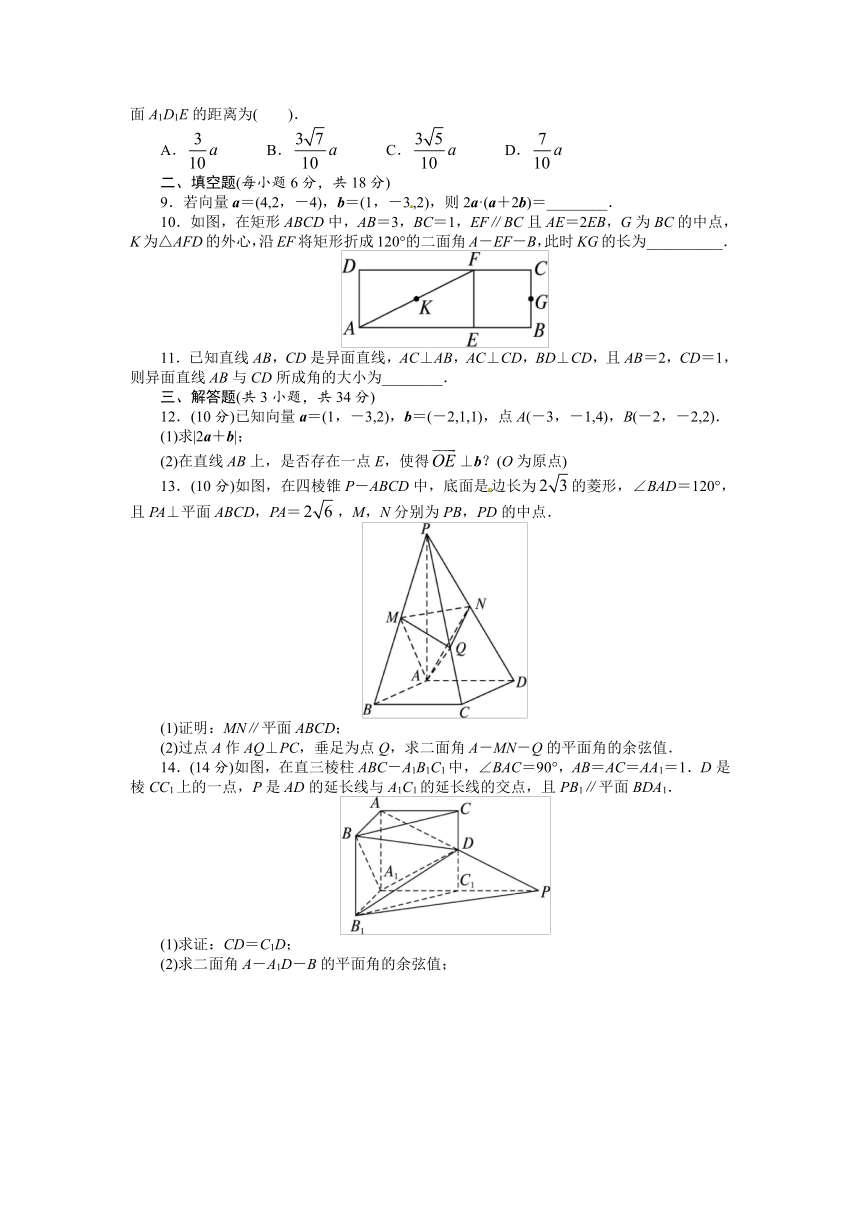
8.正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BB1,CD的中点,则点F到平面A1D1E的距离为( ).
A. B. C. D.
二、填空题(每小题6分,共18分)
9.若向量a=(4,2,-4),b=(1,-3,2),则2a·(a+2b)=________.
10.如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为△AFD的外心,沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为__________.
11.已知直线AB,CD是异面直线,AC⊥AB,AC⊥CD,BD⊥CD,且AB=2,CD=1,则异面直线AB与CD所成角的大小为________.
三、解答题(共3小题,共34分)
12.(10分)已知向量a=(1,-3,2),b=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求|2a+b|;
(2)在直线AB上,是否存在一点E,使得⊥b?(O为原点)
13.(10分)如图,在四棱锥P-ABCD中,底面是边长为的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=,M,N分别为PB,PD的中点.
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角A-MN-Q的平面角的余弦值.
14.(14分)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1.D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.
(1)求证:CD=C1D;
(2)求二面角A-A1D-B的平面角的余弦值;
参考答案
1答案:D
2答案:D 解析:a+λb=(λ,1+λ,-1).
由(a+λb)⊥a,知(a+λb)·a=0,
所以1+λ+1=0,解得λ=-2.
3答案:C 解析:由公式cos〈a,b〉=,知,解方程得λ=-2或.
4答案:A 解析:|a|=3,|b|=3,而a·b=4=|a||b|,
∴=,故=,[来源:.Com]
于是以a,b为邻边的平行四边形的面积为
S=|a||b|=.
5答案:A 解析:=++=++(-)=.
6答案:A 解析:设PA=AB=2,建立空间直角坐标系,平面PAB的一个法向量是m=(1,0,0),平面PBC的一个法向量是n=.
则cos〈m,n〉=.
∴正切值tan〈m,n〉=.
7答案:D 解析:由题意可知=λ,故可设Q(λ,λ,2λ),
∴·=6λ2-16λ+10=,
∴时,·取最小值,此时Q的坐标为.
8答案:C 解析:建立如图所示的坐标系,
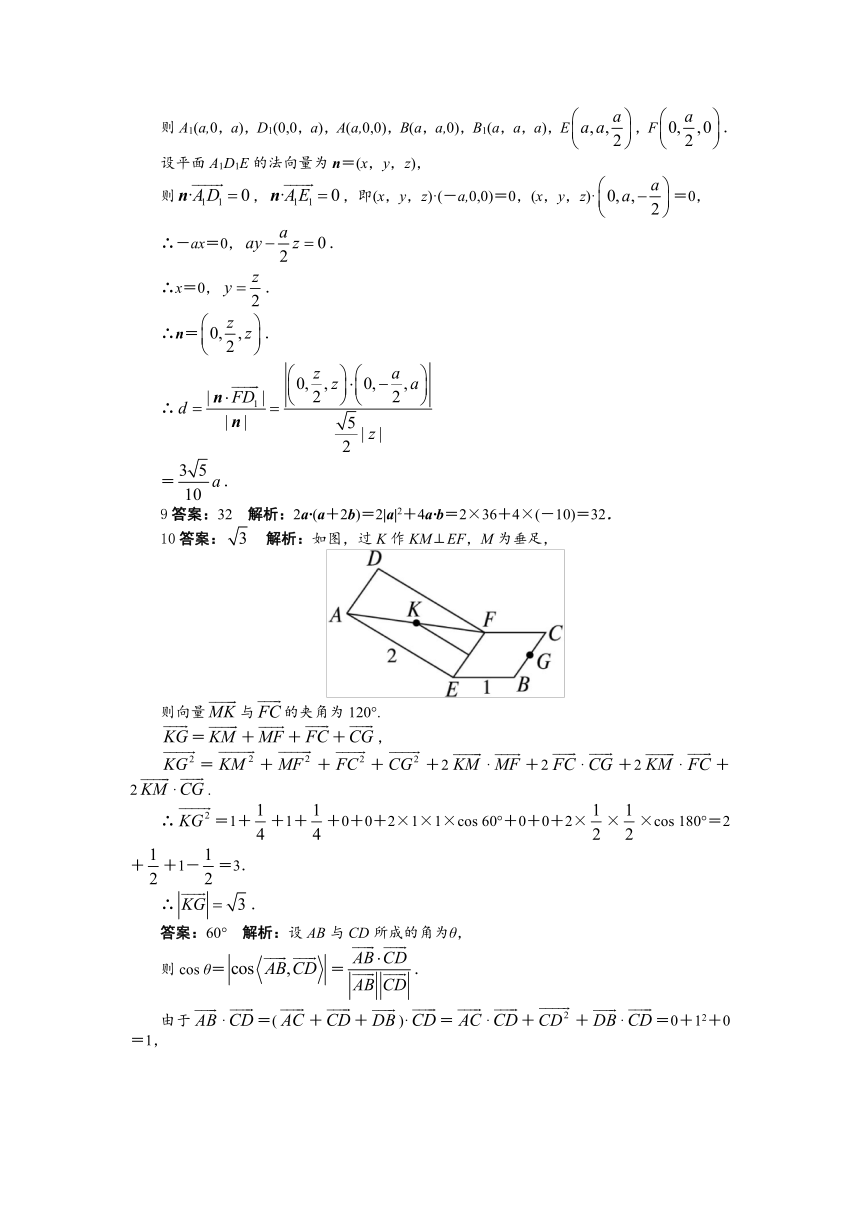
则A1(a,0,a),D1(0,0,a),A(a,0,0),B(a,a,0),B1(a,a,a),E,F.
设平面A1D1E的法向量为n=(x,y,z),
则,,即(x,y,z)·(-a,0,0)=0,(x,y,z)·=0,
∴-ax=0,.
∴x=0,.
∴n=.
∴
=.
9答案:32 解析:2a·(a+2b)=2|a|2+4a·b=2×36+4×(-10)=32.
10答案: 解析:如图,过K作KM⊥EF,M为垂足,
则向量与的夹角为120°.
=+++,
=++++2·+2·+2·+2·.
∴=1++1++0+0+2×1×1×cos 60°+0+0+2×××cos 180°=2++1-=3.
∴.
答案:60° 解析:设AB与CD所成的角为θ,
则cos θ==.
由于·=(++)·=·++·=0+12+0=1,
∴cos θ=.
由于0°<θ≤90°,∴θ=60°,故异面直线AB与CD所成角的大小为60°.
12答案:解:(1)2a+b=(2,-6,4)+(-2,1,1)=(0,-5,5),故|2a+b|=.
答案:解:=+=+t=(-3,-1,4)+t(1,-1,-2)=(-3+t,-1-t,4-2t).若⊥b,则·b=0,
所以-2(-3+t)+(-1-t)+(4-2t)=0,解得,因此存在点E,使得⊥b,此时E点坐标为.
13答案:证明:连结BD,因为M,N分别是PB,PD的中点,
所以MN是△PBD的中位线.所以MN∥BD.
又因为MN平面ABCD,BD平面ABCD,
所以MN∥平面ABCD.
答案:解法一:连结AC交BD于O,以O为原点,OC,OD所在直线为x,y轴,建立空间直角坐标系O-xyz,如图所示.
在菱形ABCD中,∠BAD=120°,得AC=AB=,BD=AB=6.
又因为PA⊥平面ABCD,所以PA⊥AC.
在直角△PAC中,,,AQ⊥PC,得QC=2,PQ=4,
由此知各点坐标如下:A(,0,0),B(0,-3,0),C(,0,0),D(0,3,0),P(,0,),M,N,Q.
设m=(x,y,z)为平面AMN的法向量.
由=,=,
知
取z=-1,得m=(,0,-1).
设n=(x,y,z)为平面QMN的法向量.
由=,
=知
取z=5,得n=(,0,5).
于是cos〈m,n〉=.
所以二面角A-MN-Q的平面角的余弦值为.
解法二:在菱形ABCD中,∠BAD=120°,得AC=AB=BC=CD=DA,BD=AB.
又因为PA⊥平面ABCD,
所以PA⊥AB,PA⊥AC,PA⊥AD.
所以PB=PC=PD.
所以△PBC≌△PDC.
而M,N分别是PB,PD的中点,
所以MQ=NQ,且AM=PB=PD=AN.
取线段MN的中点E,连结AE,EQ,
则AE⊥MN,QE⊥MN,
所以∠AEQ为二面角A-MN-Q的平面角.
由AB=,PA=,[来源:学§科§网]
故在△AMN中,AM=AN=3,MN=BD=3,得AE=.
在直角△PAC中,AQ⊥PC,得
AQ=,QC=2,PQ=4,
在△PBC中,cos∠BPC=,
得MQ=.
在等腰△MQN中,MQ=NQ=,MN=3,得
.
在△AEQ中,,,,得
cos∠AEQ=.
所以二面角A-MN-Q的平面角的余弦值为.
14答案:解:如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴、y轴、z轴建立空间直角坐标系A1xyz,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1).
[来源:学科网]
答案:解:如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴、y轴、z轴建立空间直角坐标系A1xyz,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1).
设C1D=x,∵AC∥PC1,
∴.
由此可得D(0,1,x),P,
∴=(1,0,1),=(0,1,x),
=.
设平面BA1D的一个法向量为n1=(a,b,c),[来源:学*科*网Z*X*X*K]
则
令c=-1,则n1=(1,x,-1).[来源:学。科。网]
∵PB1∥平面BA1D,
∴n1·=1×(-1)+x·+(-1)×0=0.
由此可得,故CD=C1D.
答案:解:由(1)知,平面BA1D的一个法向量n1=.
又n2=(1,0,0)为平面AA1D的一个法向量,
∴cos〈n1,n2〉=.
故二面角A-A1D-B的平面角的余弦值为.
(3)求点C到平面B1DP的距离.
答案:解:∵=(1,-2,0),=,
设平面B1DP的一个法向量n3=(a1,b1,c1),
则
令c1=1,可得n3=.
又,
∴点C到平面B1DP的距离.
(时间:45分钟,满分:100分)
一、选择题(每小题6分,共48分)
1.已知点A(-4,8,6),则点A关于y轴对称的点的坐标为( ).
A.(-4,-8,6) B.(-4,-8,-6)
C.(-6,-8,4) D.(4,8,-6)
2.若a=(0,1,-1),b=(1,1,0),且(a+λb)⊥a,则实数λ的值为( ).
A.-1 B.0 C.1 D.-2
3.若向量a=(1,λ,2),b=(2,-1,2),a,b夹角的余弦值为,则λ等于( ),
A.2 B.-2
C.-2或 D.2或
4.已知a=(2,-1,2),b=(2,2,1),则以a,b为邻边的平行四边形的面积为( ).
A. B. C.4 D.8
5.如图,在四面体ABCD中,已知=b,=a,=c,,则等于( ).
A.
B.
C.
D.
6.在三棱锥P-ABC中,△ABC为等边三角形,PA⊥平面ABC,且PA=AB,则二面角A-PB-C的平面角的正切值为( ).
A. B. C. D.
7.已知A(1,2,3),B(2,1,2),P(1,1,2),点Q在直线OP上运动(O为原点),则当取最小值时,点Q的坐标为( ).
A. B.
C. D.
8.正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BB1,CD的中点,则点F到平面A1D1E的距离为( ).
A. B. C. D.
二、填空题(每小题6分,共18分)
9.若向量a=(4,2,-4),b=(1,-3,2),则2a·(a+2b)=________.
10.如图,在矩形ABCD中,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为△AFD的外心,沿EF将矩形折成120°的二面角A-EF-B,此时KG的长为__________.
11.已知直线AB,CD是异面直线,AC⊥AB,AC⊥CD,BD⊥CD,且AB=2,CD=1,则异面直线AB与CD所成角的大小为________.
三、解答题(共3小题,共34分)
12.(10分)已知向量a=(1,-3,2),b=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).
(1)求|2a+b|;
(2)在直线AB上,是否存在一点E,使得⊥b?(O为原点)
13.(10分)如图,在四棱锥P-ABCD中,底面是边长为的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=,M,N分别为PB,PD的中点.
(1)证明:MN∥平面ABCD;
(2)过点A作AQ⊥PC,垂足为点Q,求二面角A-MN-Q的平面角的余弦值.
14.(14分)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1.D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.
(1)求证:CD=C1D;
(2)求二面角A-A1D-B的平面角的余弦值;
参考答案
1答案:D
2答案:D 解析:a+λb=(λ,1+λ,-1).
由(a+λb)⊥a,知(a+λb)·a=0,
所以1+λ+1=0,解得λ=-2.
3答案:C 解析:由公式cos〈a,b〉=,知,解方程得λ=-2或.
4答案:A 解析:|a|=3,|b|=3,而a·b=4=|a||b|,
∴=,故=,[来源:.Com]
于是以a,b为邻边的平行四边形的面积为
S=|a||b|=.
5答案:A 解析:=++=++(-)=.
6答案:A 解析:设PA=AB=2,建立空间直角坐标系,平面PAB的一个法向量是m=(1,0,0),平面PBC的一个法向量是n=.
则cos〈m,n〉=.
∴正切值tan〈m,n〉=.
7答案:D 解析:由题意可知=λ,故可设Q(λ,λ,2λ),
∴·=6λ2-16λ+10=,
∴时,·取最小值,此时Q的坐标为.
8答案:C 解析:建立如图所示的坐标系,
则A1(a,0,a),D1(0,0,a),A(a,0,0),B(a,a,0),B1(a,a,a),E,F.
设平面A1D1E的法向量为n=(x,y,z),
则,,即(x,y,z)·(-a,0,0)=0,(x,y,z)·=0,
∴-ax=0,.
∴x=0,.
∴n=.
∴
=.
9答案:32 解析:2a·(a+2b)=2|a|2+4a·b=2×36+4×(-10)=32.
10答案: 解析:如图,过K作KM⊥EF,M为垂足,
则向量与的夹角为120°.
=+++,
=++++2·+2·+2·+2·.
∴=1++1++0+0+2×1×1×cos 60°+0+0+2×××cos 180°=2++1-=3.
∴.
答案:60° 解析:设AB与CD所成的角为θ,
则cos θ==.
由于·=(++)·=·++·=0+12+0=1,
∴cos θ=.
由于0°<θ≤90°,∴θ=60°,故异面直线AB与CD所成角的大小为60°.
12答案:解:(1)2a+b=(2,-6,4)+(-2,1,1)=(0,-5,5),故|2a+b|=.
答案:解:=+=+t=(-3,-1,4)+t(1,-1,-2)=(-3+t,-1-t,4-2t).若⊥b,则·b=0,
所以-2(-3+t)+(-1-t)+(4-2t)=0,解得,因此存在点E,使得⊥b,此时E点坐标为.
13答案:证明:连结BD,因为M,N分别是PB,PD的中点,
所以MN是△PBD的中位线.所以MN∥BD.
又因为MN平面ABCD,BD平面ABCD,
所以MN∥平面ABCD.
答案:解法一:连结AC交BD于O,以O为原点,OC,OD所在直线为x,y轴,建立空间直角坐标系O-xyz,如图所示.
在菱形ABCD中,∠BAD=120°,得AC=AB=,BD=AB=6.
又因为PA⊥平面ABCD,所以PA⊥AC.
在直角△PAC中,,,AQ⊥PC,得QC=2,PQ=4,
由此知各点坐标如下:A(,0,0),B(0,-3,0),C(,0,0),D(0,3,0),P(,0,),M,N,Q.
设m=(x,y,z)为平面AMN的法向量.
由=,=,
知
取z=-1,得m=(,0,-1).
设n=(x,y,z)为平面QMN的法向量.
由=,
=知
取z=5,得n=(,0,5).
于是cos〈m,n〉=.
所以二面角A-MN-Q的平面角的余弦值为.
解法二:在菱形ABCD中,∠BAD=120°,得AC=AB=BC=CD=DA,BD=AB.
又因为PA⊥平面ABCD,
所以PA⊥AB,PA⊥AC,PA⊥AD.
所以PB=PC=PD.
所以△PBC≌△PDC.
而M,N分别是PB,PD的中点,
所以MQ=NQ,且AM=PB=PD=AN.
取线段MN的中点E,连结AE,EQ,
则AE⊥MN,QE⊥MN,
所以∠AEQ为二面角A-MN-Q的平面角.
由AB=,PA=,[来源:学§科§网]
故在△AMN中,AM=AN=3,MN=BD=3,得AE=.
在直角△PAC中,AQ⊥PC,得
AQ=,QC=2,PQ=4,
在△PBC中,cos∠BPC=,
得MQ=.
在等腰△MQN中,MQ=NQ=,MN=3,得
.
在△AEQ中,,,,得
cos∠AEQ=.
所以二面角A-MN-Q的平面角的余弦值为.
14答案:解:如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴、y轴、z轴建立空间直角坐标系A1xyz,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1).
[来源:学科网]
答案:解:如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴、y轴、z轴建立空间直角坐标系A1xyz,则A1(0,0,0),B1(1,0,0),C1(0,1,0),B(1,0,1).
设C1D=x,∵AC∥PC1,
∴.
由此可得D(0,1,x),P,
∴=(1,0,1),=(0,1,x),
=.
设平面BA1D的一个法向量为n1=(a,b,c),[来源:学*科*网Z*X*X*K]
则
令c=-1,则n1=(1,x,-1).[来源:学。科。网]
∵PB1∥平面BA1D,
∴n1·=1×(-1)+x·+(-1)×0=0.
由此可得,故CD=C1D.
答案:解:由(1)知,平面BA1D的一个法向量n1=.
又n2=(1,0,0)为平面AA1D的一个法向量,
∴cos〈n1,n2〉=.
故二面角A-A1D-B的平面角的余弦值为.
(3)求点C到平面B1DP的距离.
答案:解:∵=(1,-2,0),=,
设平面B1DP的一个法向量n3=(a1,b1,c1),
则
令c1=1,可得n3=.
又,
∴点C到平面B1DP的距离.
