高中数学选择性必修第一册人教A版(2019)2.2.3 一般式方程 课件(共33张PPT)
文档属性
| 名称 | 高中数学选择性必修第一册人教A版(2019)2.2.3 一般式方程 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 743.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 22:16:12 | ||
图片预览











文档简介
(共33张PPT)
第二章 2.2.3一般式方程
1.掌握直线的一般式方程;
2.理解关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示直线;
3.会进行直线方程的五种形式之间的转化.
问题导学
题型探究
达标检测
学习目标
问题导学 新知探究 点点落实
知识点一 直线的一般式方程
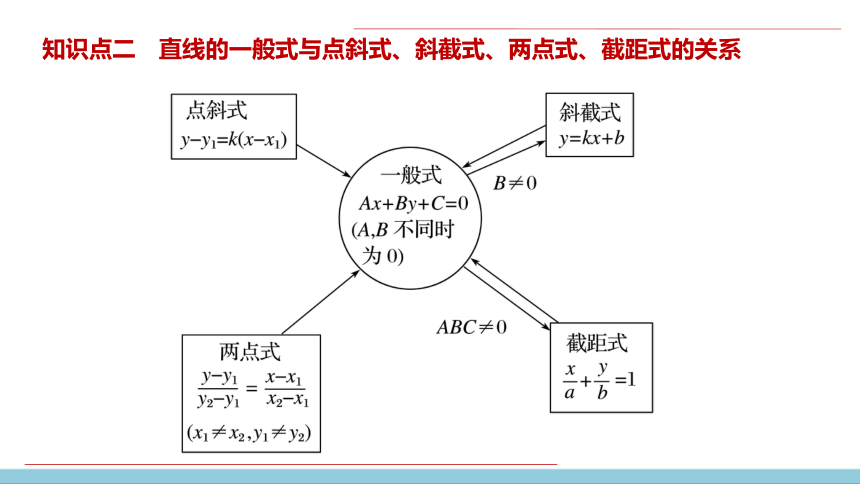
思考1 直线的点斜式、斜截式、两点式、截距式这四种形式都能用Ax+By+C=0(A,B不同时为0)来表示吗?
答案 能.
思考2 关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)一定表示直线吗?
答案 一定.
思考3 当B≠0时,方程Ax+By+C=0(A,B不同时为0)表示怎样的直线?B=0呢?
形式
条件 A,B
Ax+By+C=0
不同时为0
所以该方程表示一条垂直于x轴的直线.
知识点二 直线的一般式与点斜式、斜截式、两点式、截距式的关系
题型探究 重点难点 个个击破
类型一 直线一般式的性质
例1 设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
(1)若直线l在x轴上的截距为-3,则m=________.
解析 令y=0,
得m= 或m=3(舍去).
∴m= .
(2)若直线l的斜率为1,则m=________.
-2
解析 由直线l化为斜截式方程
得m=-2或m=-1(舍去).
∴m=-2.
反思与感悟
(1)方程Ax+By+C=0表示直线,需满足A,B不同时为0.
(2)令x=0可得在y轴上的截距.令y=0可得在x轴上的截距.若确定直线斜率存在,可将一般式化为斜截式.
(3)解分式方程注意验根.
跟踪训练1 (1)若方程(a2+5a+6)x+(a2+2a)y+1=0表示一条直线,则实数a满足________.
得a=-2,
∵方程(a2+5a+6)x+(a2+2a)y+1=0表示一条直线,
∴a≠-2.
a≠-2
(2)直线l的方程为(a+1)x+y+2-a=0,
①若l在两坐标轴上的截距相等,求a;
解 令x=0,则y=a-2,
令y=0,则
∵l在两坐标轴上的截距相等,
得a=2或a=0.
②若l不经过第二象限,求实数a的取值范围.
解 由①知,在x轴上截距为
在y轴上的截距为a-2,
得a<-1或a=2.
类型二 判断两条直线的位置关系
例2 判断下列直线的位置关系:
(1)l1:2x-3y+4=0,l2:3y-2x+4=0;
解 直线l2的方程可写为-2x+3y+4=0,
(2)l1:2x-3y+4=0,l2:-4x+6y-8=0;
∴l1与l2重合.
∴l1∥l2.
(3)l1:(-a-1)x+y=5,l2:2x+(2a+2)y+4=0.
解 由题意知,当a=-1时,
l1:y=5,l2:x+2=0,
∴l1⊥l2.
当a≠-1时,
故l1不平行于l2,
又(-a-1)×2+(2a+2)×1=0,
∴l1⊥l2,综上l1⊥l2.
反思与感悟
(1)当直线方程中存在字母参数时,不仅要考虑到斜率存在的一般情况,也要考虑到斜率不存在的特殊情况.同时还要注意x、y的系数不能同时为零这一隐含条件.
(2)在判断两直线平行、垂直时,也可直接利用直线方程的系数间的关系得出结论.
跟踪训练2 (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
解 方法一
由l1:2x+(m+1)y+4=0,l2:mx+3y-2=0知:
①当m=0时,显然l1与l2不平行.
解得m=2或m=-3,
∴m的值为2或-3.
方法二
令2×3=m(m+1),
解得m=-3或m=2.
当m=-3时,
l1:x-y+2=0,l2:3x-3y+2=0,
显然l1与l2不重合,∴l1∥l2.
同理当m=2时,
l1:2x+3y+4=0,l2:2x+3y-2=0,
显然l1与l2不重合,∴l1∥l2.
∴m的值为2或-3.
(2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线
l2:(a-1)x+(2a+3)y+2=0互相垂直?
解 方法一
由题意知,直线l1⊥l2.
①若1-a=0,即a=1时,
直线l1:3x-1=0与直线l2:5y+2=0显然垂直.
②若2a+3=0,即a= 时,
直线l1:x+5y-2=0与直线l2:5x-4=0不垂直.
③若1-a≠0,且2a+3≠0,
则直线l1,l2的斜率k1,k2都存在,
当l1⊥l2时,k1·k2=-1,
∴a=-1.
综上可知,当a=1或a=-1时,
直线l1⊥l2.
方法二
由题意知直线l1⊥l2,
∴(a+2)(a-1)+(1-a)(2a+3)=0,
解得a=±1,
将a=±1代入方程,均满足题意.
故当a=1或a=-1时,直线l1⊥l2.
类型三 求平行、垂直的直线方程
例3 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(1)过点(-1,3),且与l平行;
(2)过点(-1,3),且与l垂直.
解 方法一 l的方程可化为
∴l的斜率为
(1) ∵l′与l平行,
∴l′的斜率为- 又∵l′过点(-1,3),
即3x+4y-9=0.
(2) ∵l′与l垂直,
又l′过点(-1,3),
即4x-3y+13=0.
方法二 (1) 由l′与l平行,
可设l′的方程为3x+4y+m=0.
将点(-1,3)代入上式得m=-9.
∴所求直线的方程为3x+4y-9=0.
(2) 由l′与l垂直,
可设l′的方程为4x-3y+n=0.
将(-1,3)代入上式得n=13.
∴所求直线的方程为4x-3y+13=0.
反思与感悟
一般地,直线Ax+By+C=0中系数A、B确定直线的斜率,因此,与直线Ax+By+C=0平行的直线方程可设为Ax+By+m=0,与直线Ax+By+C=0垂直的直线方程可设为Bx-Ay+n=0.这是经常采用的解题技巧.
跟踪训练3 已知点A(2,2)和直线l:3x+4y-20=0.
求:(1)过点A和直线l平行的直线方程;
解 将与直线l平行的直线方程设为3x+4y+C1=0,
又过点A(2,2),
所以3×2+4×2+C1=0,
所以C1=-14.
所求直线方程为3x+4y-14=0.
(2)过点A和直线l垂直的直线方程.
解 将与l垂直的直线方程设为4x-3y+C2=0,
又过点A(2,2),
所以4×2-3×2+C2=0,
所以C2=-2,
所以直线方程为4x-3y-2=0.
1
2
3
达标检测
4
1.若方程Ax+By+C=0表示直线,则A、B应满足的条件为( )
A.A≠0 B.B≠0
C.A·B≠0 D.A2+B2≠0
解析 方程Ax+By+C=0表示直线的条件为A、B不能同时为0,即A2+B2≠0.
D
1
2
3
4
2.已知ab<0,bc<0,则直线ax+by=c通过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
C
解析 由ax+by=c,
∵ab<0,bc<0,
∴直线的斜率k=
直线在y轴上的截距
由此可知直线通过第一、三、四象限.
1
2
3
4
3.已知两直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,
(1)若l1∥l2,则m=________.
-1
得m=-1.
(2)若l1⊥l2,则m=________.
解析 由题意知1×(m-2)+m×3=0,
得m= .
1
2
3
4
4.求与直线3x+4y+1=0平行,且过点(1,2)的直线l的方程.
解 由题意,设l的方程为3x+4y+C=0,
将点(1,2)代入l的方程
3+4×2+C=0 得C=-11,
∴直线l的方程为3x+4y-11=0.
规律与方法
1.根据两直线的一般式方程判定两直线平行的方法
(1)判定斜率是否存在,若存在,化成斜截式后,则k1=k2且b1≠b2;若都不存在,则还要判定不重合.
(2)可直接采用如下方法:
一般地,设直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.
l1∥l2 A1B2-A2B1=0,且B1C2-B2C1≠0,或A1C2-A2C1≠0.
这种判定方法避开了斜率存在和不存在两种情况的讨论,可以减小因考虑不周而造成失误的可能性.
2.根据两直线的一般式方程判定两直线垂直的方法
(1)若一个斜率为零,另一个不存在,则垂直;若两个都存在斜率,化成斜截式后,则k1k2=-1.
(2)一般地,设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,l1⊥l2 A1A2+B1B2=0.
第二种方法可避免讨论,减小失误.
第二章 2.2.3一般式方程
1.掌握直线的一般式方程;
2.理解关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)都表示直线;
3.会进行直线方程的五种形式之间的转化.
问题导学
题型探究
达标检测
学习目标
问题导学 新知探究 点点落实
知识点一 直线的一般式方程
思考1 直线的点斜式、斜截式、两点式、截距式这四种形式都能用Ax+By+C=0(A,B不同时为0)来表示吗?
答案 能.
思考2 关于x,y的二元一次方程Ax+By+C=0(A,B不同时为0)一定表示直线吗?
答案 一定.
思考3 当B≠0时,方程Ax+By+C=0(A,B不同时为0)表示怎样的直线?B=0呢?
形式
条件 A,B
Ax+By+C=0
不同时为0
所以该方程表示一条垂直于x轴的直线.
知识点二 直线的一般式与点斜式、斜截式、两点式、截距式的关系
题型探究 重点难点 个个击破
类型一 直线一般式的性质
例1 设直线l的方程为(m2-2m-3)x-(2m2+m-1)y+6-2m=0.
(1)若直线l在x轴上的截距为-3,则m=________.
解析 令y=0,
得m= 或m=3(舍去).
∴m= .
(2)若直线l的斜率为1,则m=________.
-2
解析 由直线l化为斜截式方程
得m=-2或m=-1(舍去).
∴m=-2.
反思与感悟
(1)方程Ax+By+C=0表示直线,需满足A,B不同时为0.
(2)令x=0可得在y轴上的截距.令y=0可得在x轴上的截距.若确定直线斜率存在,可将一般式化为斜截式.
(3)解分式方程注意验根.
跟踪训练1 (1)若方程(a2+5a+6)x+(a2+2a)y+1=0表示一条直线,则实数a满足________.
得a=-2,
∵方程(a2+5a+6)x+(a2+2a)y+1=0表示一条直线,
∴a≠-2.
a≠-2
(2)直线l的方程为(a+1)x+y+2-a=0,
①若l在两坐标轴上的截距相等,求a;
解 令x=0,则y=a-2,
令y=0,则
∵l在两坐标轴上的截距相等,
得a=2或a=0.
②若l不经过第二象限,求实数a的取值范围.
解 由①知,在x轴上截距为
在y轴上的截距为a-2,
得a<-1或a=2.
类型二 判断两条直线的位置关系
例2 判断下列直线的位置关系:
(1)l1:2x-3y+4=0,l2:3y-2x+4=0;
解 直线l2的方程可写为-2x+3y+4=0,
(2)l1:2x-3y+4=0,l2:-4x+6y-8=0;
∴l1与l2重合.
∴l1∥l2.
(3)l1:(-a-1)x+y=5,l2:2x+(2a+2)y+4=0.
解 由题意知,当a=-1时,
l1:y=5,l2:x+2=0,
∴l1⊥l2.
当a≠-1时,
故l1不平行于l2,
又(-a-1)×2+(2a+2)×1=0,
∴l1⊥l2,综上l1⊥l2.
反思与感悟
(1)当直线方程中存在字母参数时,不仅要考虑到斜率存在的一般情况,也要考虑到斜率不存在的特殊情况.同时还要注意x、y的系数不能同时为零这一隐含条件.
(2)在判断两直线平行、垂直时,也可直接利用直线方程的系数间的关系得出结论.
跟踪训练2 (1)已知直线l1:2x+(m+1)y+4=0与直线l2:mx+3y-2=0平行,求m的值;
解 方法一
由l1:2x+(m+1)y+4=0,l2:mx+3y-2=0知:
①当m=0时,显然l1与l2不平行.
解得m=2或m=-3,
∴m的值为2或-3.
方法二
令2×3=m(m+1),
解得m=-3或m=2.
当m=-3时,
l1:x-y+2=0,l2:3x-3y+2=0,
显然l1与l2不重合,∴l1∥l2.
同理当m=2时,
l1:2x+3y+4=0,l2:2x+3y-2=0,
显然l1与l2不重合,∴l1∥l2.
∴m的值为2或-3.
(2)当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线
l2:(a-1)x+(2a+3)y+2=0互相垂直?
解 方法一
由题意知,直线l1⊥l2.
①若1-a=0,即a=1时,
直线l1:3x-1=0与直线l2:5y+2=0显然垂直.
②若2a+3=0,即a= 时,
直线l1:x+5y-2=0与直线l2:5x-4=0不垂直.
③若1-a≠0,且2a+3≠0,
则直线l1,l2的斜率k1,k2都存在,
当l1⊥l2时,k1·k2=-1,
∴a=-1.
综上可知,当a=1或a=-1时,
直线l1⊥l2.
方法二
由题意知直线l1⊥l2,
∴(a+2)(a-1)+(1-a)(2a+3)=0,
解得a=±1,
将a=±1代入方程,均满足题意.
故当a=1或a=-1时,直线l1⊥l2.
类型三 求平行、垂直的直线方程
例3 已知直线l的方程为3x+4y-12=0,求满足下列条件的直线l′的方程:
(1)过点(-1,3),且与l平行;
(2)过点(-1,3),且与l垂直.
解 方法一 l的方程可化为
∴l的斜率为
(1) ∵l′与l平行,
∴l′的斜率为- 又∵l′过点(-1,3),
即3x+4y-9=0.
(2) ∵l′与l垂直,
又l′过点(-1,3),
即4x-3y+13=0.
方法二 (1) 由l′与l平行,
可设l′的方程为3x+4y+m=0.
将点(-1,3)代入上式得m=-9.
∴所求直线的方程为3x+4y-9=0.
(2) 由l′与l垂直,
可设l′的方程为4x-3y+n=0.
将(-1,3)代入上式得n=13.
∴所求直线的方程为4x-3y+13=0.
反思与感悟
一般地,直线Ax+By+C=0中系数A、B确定直线的斜率,因此,与直线Ax+By+C=0平行的直线方程可设为Ax+By+m=0,与直线Ax+By+C=0垂直的直线方程可设为Bx-Ay+n=0.这是经常采用的解题技巧.
跟踪训练3 已知点A(2,2)和直线l:3x+4y-20=0.
求:(1)过点A和直线l平行的直线方程;
解 将与直线l平行的直线方程设为3x+4y+C1=0,
又过点A(2,2),
所以3×2+4×2+C1=0,
所以C1=-14.
所求直线方程为3x+4y-14=0.
(2)过点A和直线l垂直的直线方程.
解 将与l垂直的直线方程设为4x-3y+C2=0,
又过点A(2,2),
所以4×2-3×2+C2=0,
所以C2=-2,
所以直线方程为4x-3y-2=0.
1
2
3
达标检测
4
1.若方程Ax+By+C=0表示直线,则A、B应满足的条件为( )
A.A≠0 B.B≠0
C.A·B≠0 D.A2+B2≠0
解析 方程Ax+By+C=0表示直线的条件为A、B不能同时为0,即A2+B2≠0.
D
1
2
3
4
2.已知ab<0,bc<0,则直线ax+by=c通过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
C
解析 由ax+by=c,
∵ab<0,bc<0,
∴直线的斜率k=
直线在y轴上的截距
由此可知直线通过第一、三、四象限.
1
2
3
4
3.已知两直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,
(1)若l1∥l2,则m=________.
-1
得m=-1.
(2)若l1⊥l2,则m=________.
解析 由题意知1×(m-2)+m×3=0,
得m= .
1
2
3
4
4.求与直线3x+4y+1=0平行,且过点(1,2)的直线l的方程.
解 由题意,设l的方程为3x+4y+C=0,
将点(1,2)代入l的方程
3+4×2+C=0 得C=-11,
∴直线l的方程为3x+4y-11=0.
规律与方法
1.根据两直线的一般式方程判定两直线平行的方法
(1)判定斜率是否存在,若存在,化成斜截式后,则k1=k2且b1≠b2;若都不存在,则还要判定不重合.
(2)可直接采用如下方法:
一般地,设直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.
l1∥l2 A1B2-A2B1=0,且B1C2-B2C1≠0,或A1C2-A2C1≠0.
这种判定方法避开了斜率存在和不存在两种情况的讨论,可以减小因考虑不周而造成失误的可能性.
2.根据两直线的一般式方程判定两直线垂直的方法
(1)若一个斜率为零,另一个不存在,则垂直;若两个都存在斜率,化成斜截式后,则k1k2=-1.
(2)一般地,设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,l1⊥l2 A1A2+B1B2=0.
第二种方法可避免讨论,减小失误.
