沪科版七年级数学上册4.3 线段的长短比较 导学课件(共35张PPT)
文档属性
| 名称 | 沪科版七年级数学上册4.3 线段的长短比较 导学课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-17 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
4.3 线段的长短比较
第4章 直线与角
逐点
学练
本节小结
作业提升
本节要点
1
学习流程
2
线段的长短比较
线段的和差倍分
线段的中点
线段的基本事实
知识点
线段的长短比较
1
1. 度量法 利用刻度尺分别测量出两条线段的长度,然后根据测量结果进行比较.
2. 叠合法 把两条线段中的一条线段移到另一条线段上,使它们有一个端点重合,然后根据另一个端点的位置进行比较.
例如:比较线段AB,CD 的长短,可以把它们移到同一条直线上,使一个端点A 和C 重合,另一个端点B 和D 落在点A 的同一侧,如图4.3-1.
特别解读
当两条线段的长短差别不大,而又不便放在一起比较时,
运用度量法;当两条线段能够放在一起而又不需要知道
相差的具体数值时,可用叠合法.
度量法和叠合法分别是从“数”和“形”两个方面出发的,从“数”的方面比较,一般用度量法;从“形”的方面比较,一般用叠合法.
如图4.3-2 是一张三角形纸片,你能比较线段AB与线段BC 的长短吗?
例 1
解题秘方:可以利用度量法,分别量出每条线段的长度,
然后进行比较,或者利用叠合法进行比较.
方法点拨
比较有公共端点的两条线段的长短的方法:
1.借助刻度尺进行度量;
2.借助圆规进行叠合.
解:方法一:度量法.
用刻度尺量得AB=1.7 cm,BC=1.3 cm,
所以AB>BC.
方法二:叠合法. 如图4.3-2,将圆规的一端放在B 点,
另一端放在C 点,将圆规绕B 点旋转,圆弧与AB 交于D 点.所以AB>BC.
知识点
线段的和差倍分
2
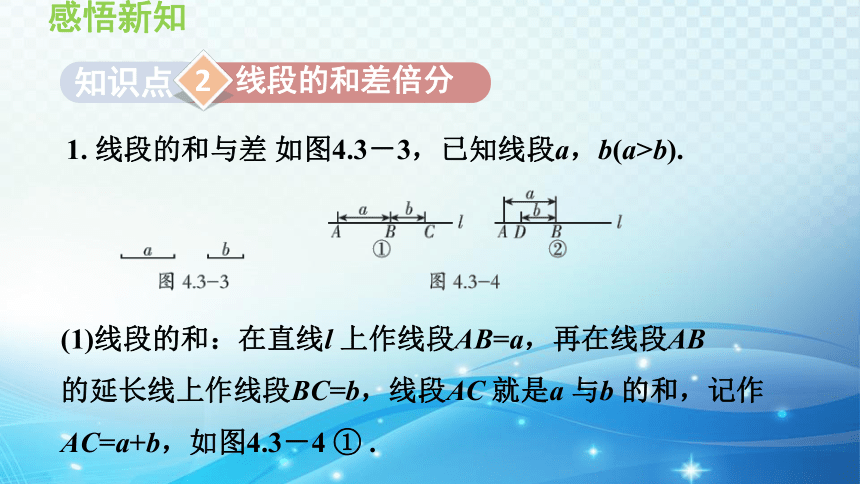
1. 线段的和与差 如图4.3-3,已知线段a,b(a>b).
(1)线段的和:在直线l 上作线段AB=a,再在线段AB
的延长线上作线段BC=b,线段AC 就是a 与b 的和,记作
AC=a+b,如图4.3-4 ① .
(2)线段的差:在直线l 上作线段AB=a,在线段AB 上
作线段BD=b,则线段AD 就是a 与b 的差,记作AD=a-b,如图4.3-4 ② .
2. 线段的倍与分 如图4.3-5,射线AE 上有B,C,D 三点,线段AB,BC,CD 的长度关系是AB=BC=CD, 则AC=2BC,AD=3AB,AB= AC,AB= AD,AC= AD.
特别提醒
几何中线段的和差与代数中的数的和差有联系也有区别,在数量上是线段长度的和差,在图形上作线段的和差得到的图形是一条线段.
用尺规作线段的和时,依次向右截取;作线段的差时,从最右边的端点向左截取.
如图4.3-6,已知点B,C 在线段AD 上.
(1)图中共有 ______条线段.
(2)已知AB=CD.
①比较线段的长短:AC____BD(填“>”“=”或“<”);
②若BD=4AB,BC=12 cm,则AD=____cm.
例2
解题秘方:本题主要考查了线段长度的计算,解题关键是掌握线段的和、差、倍、分及计算方法.
特别提醒
在将两条线段用“>”“<”或“=”连接起来的时候,字母前的“线段”两字就省略不写了.只有线段才能比较长短,而直线、射线不能比较长短.
解:(1)图中的线段有AB,BC,CD,AC,BD,AD,
共6 条.
(2)①因为AB=CD,所以AB+BC=CD+BC,即AC=BD.
②因为BD=4AB,AB=CD,所以BC=3AB. 因为BC=12 cm,所以AB=4 cm,所以AD=AB+BD=4+4×4=20(cm).
答案:(1)6 (2)① = ② 20
知识点
线段的中点
3
1. 线段的中点的定义
把一条线段分成两条相等线段的点叫做线段的中点. 如图
4.3-7,若M 是线段AB 的中点,则有AM=BM= AB.
特别提醒
线段的中点表示法:线段的中点一定在线段上,点M为线段AB的中点有三种表达方式:
(1)点M在线段AB上,且AM=BM;
(2)AB=2AM=2BM;
(3)AM=BM= AB.线段的中点只有一个,且一定在线段上,类似地,线段的三等分点有两个、线段的四等分点有三个,且这些点都在线段上.
2. 等分线段
(1)把一条线段分成三条相等的线段的点叫做线段的三
等分点. 如图4.3-8,若M,N 是线段AB 的三等分点,则有AM=MN=NB= AB.
(2)把一条线段分成四条相等的线段的点叫做线段的四等分点. 如图4.3-9,若M,N,P 是线段AB 的四等分点,则有AM=MN=NP=PB= AB.
如图4.3-10,M 是线段AC 的中点,点B 在线段
AC 上,且AB=4,BC=2AB,求线段MC 和线段BM 的长.
例 3
解题秘方:紧扣中点的意义及要求的线段与已知线段之间的数量关系,求线段长.
方法点拨
利用“逐段计算法”求线段长:
要求某条线段的长,先确定这条线段等于哪几条线段的和或差,分析这些线段的长度是已知的,还是要通过别的条件再求的,再进行逐段计算.
解:因为AB=4,BC=2AB,所以BC=8.
所以AC=AB+BC=4+8=12.
因为M 是线段AC 的中点,
所以MC=AM= AC=6.
所以BM=AM-AB=6-4=2.
如图4.3-11, 已知B,C 两点把线段AD 分成
2 ∶ 5 ∶ 3 三部分,点M 为AD 的中点,BM=6 cm,求CM 和AD 的长.
例4
解题秘方:利用已知条件BM=6 cm 作为等量关系列出方
程,求出CM 和AD 的长.
方法点拨
利用方程思想求线段的长的方法:
当利用逐段计算法难以求出线段长时,可考虑运用方程思想,将其中已知的线段长作为等量关系,设出要求的线段长,用含要求线段长的式子表示已知线段长(利用它们之间的数量关系表示),列出方程解决问题.
解:设AB=2x cm,则BC=5x cm,CD=3x cm.
所以AD=AB+BC+CD=10x cm.
因为M 是AD 的中点,
所以AM=MD= AD= ×10x=5x(cm).
因为BM=AM-AB,所以5x-2x=6. 所以x=2.
所以CM=MD-CD=5x-3x=2x=2×2=4(cm),
AD=10x=10×2=20(cm).
知识点
线段的基本事实
4
线段的基本事实 两点间的距离 举例
两点之间的所有连线中,线段最短. 简单说成:两点之间,线段最短 定义 性质
在所有连接A,B 两点的线中,线段AB 是最短的,线段AB 的长度就是点A与点B 之间的距离
两点之间线段的长度,叫做这两点之间的距离 (1)存在性; (2)最短性; (3)唯一性
警示误区
两点间的距离是一个具体的数量,而线段本身是图形. 因此不能把A,B 两点间的距离说成是线段AB. 另外, 连接两点是指画出以这两点端点的线段.
在同一所学校上学的小明、小亮、小红三位同学
分别住在A,B,C 三个住宅区,如图4.3-12,A,B,C 三点共线,且AB=40 m,BC=100 m,他们打算合租一辆车去上学. 由于车位紧张,他们准备在三个住宅区之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在何处?
例 5
解题秘方:根据停靠点的不同位置,分别计算他们步行
到停靠点的路程之和,再进行比较,确定位置.
技巧点拨
在解答某些数学问题时,有时会遇到多种情况,需要对各种情况加以分类,并逐类求解,然后综合得解,这就是分类讨论法,如本题中应分情况讨论车的停靠点.
解:AC=AB+BC=40+100=140(m).
分情况讨论如下:
(1)若停靠点设在A 住宅区,则他们的路程总和为
40+140=180(m);
(2)若停靠点设在A 住宅区与B 住宅区之间(不包括A,B 住宅区),则他们的路程总和大于140 m且小于180 m;
(3)若停靠点设在B 住宅区,则他们的路程总和为140 m;
(4)若停靠点设在B 住宅区与C 住宅区之间(不包括
B,C 住宅区),则他们的路程总和大于140 m且小于240 m;
(5)若停靠点设在C 住宅区,则他们的路程总和为
140+100=240(m).
综上所述,为使三位同学步行到停靠点的路程之和最小,
停靠点应设在B 住宅区.
详解
当停靠点位于A,B 之间时,不妨记为点D,如图4.3-13,则AD+DB=AB=40 m,100米=BC如图4.3-14,有一个正方体盒子放在桌面上,一只虫子在顶点A 处,一只蜘蛛在顶点B 处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,应该怎样走?
你能画出来吗?
与你的同伴交流一下.
例6
解题秘方:蜘蛛要想最快地捉住虫子,需走最短的路线,
而蜘蛛走的路线在正方体的表面上,因此应在正方体
的表面展开图中寻找.
解: 有四种走法, 分别是B → F → A,B → G → A,
B → M → A,B → N → A(F,G,M,N 分别为DE,CD,
KE,KH 的中点),如图4.3-15.
线段、射线、直线
三线(线段、射线、直线)
直线的确定性
定义
表示方法
端点数
请完成教材课后习题
作业提升
4.3 线段的长短比较
第4章 直线与角
逐点
学练
本节小结
作业提升
本节要点
1
学习流程
2
线段的长短比较
线段的和差倍分
线段的中点
线段的基本事实
知识点
线段的长短比较
1
1. 度量法 利用刻度尺分别测量出两条线段的长度,然后根据测量结果进行比较.
2. 叠合法 把两条线段中的一条线段移到另一条线段上,使它们有一个端点重合,然后根据另一个端点的位置进行比较.
例如:比较线段AB,CD 的长短,可以把它们移到同一条直线上,使一个端点A 和C 重合,另一个端点B 和D 落在点A 的同一侧,如图4.3-1.
特别解读
当两条线段的长短差别不大,而又不便放在一起比较时,
运用度量法;当两条线段能够放在一起而又不需要知道
相差的具体数值时,可用叠合法.
度量法和叠合法分别是从“数”和“形”两个方面出发的,从“数”的方面比较,一般用度量法;从“形”的方面比较,一般用叠合法.
如图4.3-2 是一张三角形纸片,你能比较线段AB与线段BC 的长短吗?
例 1
解题秘方:可以利用度量法,分别量出每条线段的长度,
然后进行比较,或者利用叠合法进行比较.
方法点拨
比较有公共端点的两条线段的长短的方法:
1.借助刻度尺进行度量;
2.借助圆规进行叠合.
解:方法一:度量法.
用刻度尺量得AB=1.7 cm,BC=1.3 cm,
所以AB>BC.
方法二:叠合法. 如图4.3-2,将圆规的一端放在B 点,
另一端放在C 点,将圆规绕B 点旋转,圆弧与AB 交于D 点.所以AB>BC.
知识点
线段的和差倍分
2
1. 线段的和与差 如图4.3-3,已知线段a,b(a>b).
(1)线段的和:在直线l 上作线段AB=a,再在线段AB
的延长线上作线段BC=b,线段AC 就是a 与b 的和,记作
AC=a+b,如图4.3-4 ① .
(2)线段的差:在直线l 上作线段AB=a,在线段AB 上
作线段BD=b,则线段AD 就是a 与b 的差,记作AD=a-b,如图4.3-4 ② .
2. 线段的倍与分 如图4.3-5,射线AE 上有B,C,D 三点,线段AB,BC,CD 的长度关系是AB=BC=CD, 则AC=2BC,AD=3AB,AB= AC,AB= AD,AC= AD.
特别提醒
几何中线段的和差与代数中的数的和差有联系也有区别,在数量上是线段长度的和差,在图形上作线段的和差得到的图形是一条线段.
用尺规作线段的和时,依次向右截取;作线段的差时,从最右边的端点向左截取.
如图4.3-6,已知点B,C 在线段AD 上.
(1)图中共有 ______条线段.
(2)已知AB=CD.
①比较线段的长短:AC____BD(填“>”“=”或“<”);
②若BD=4AB,BC=12 cm,则AD=____cm.
例2
解题秘方:本题主要考查了线段长度的计算,解题关键是掌握线段的和、差、倍、分及计算方法.
特别提醒
在将两条线段用“>”“<”或“=”连接起来的时候,字母前的“线段”两字就省略不写了.只有线段才能比较长短,而直线、射线不能比较长短.
解:(1)图中的线段有AB,BC,CD,AC,BD,AD,
共6 条.
(2)①因为AB=CD,所以AB+BC=CD+BC,即AC=BD.
②因为BD=4AB,AB=CD,所以BC=3AB. 因为BC=12 cm,所以AB=4 cm,所以AD=AB+BD=4+4×4=20(cm).
答案:(1)6 (2)① = ② 20
知识点
线段的中点
3
1. 线段的中点的定义
把一条线段分成两条相等线段的点叫做线段的中点. 如图
4.3-7,若M 是线段AB 的中点,则有AM=BM= AB.
特别提醒
线段的中点表示法:线段的中点一定在线段上,点M为线段AB的中点有三种表达方式:
(1)点M在线段AB上,且AM=BM;
(2)AB=2AM=2BM;
(3)AM=BM= AB.线段的中点只有一个,且一定在线段上,类似地,线段的三等分点有两个、线段的四等分点有三个,且这些点都在线段上.
2. 等分线段
(1)把一条线段分成三条相等的线段的点叫做线段的三
等分点. 如图4.3-8,若M,N 是线段AB 的三等分点,则有AM=MN=NB= AB.
(2)把一条线段分成四条相等的线段的点叫做线段的四等分点. 如图4.3-9,若M,N,P 是线段AB 的四等分点,则有AM=MN=NP=PB= AB.
如图4.3-10,M 是线段AC 的中点,点B 在线段
AC 上,且AB=4,BC=2AB,求线段MC 和线段BM 的长.
例 3
解题秘方:紧扣中点的意义及要求的线段与已知线段之间的数量关系,求线段长.
方法点拨
利用“逐段计算法”求线段长:
要求某条线段的长,先确定这条线段等于哪几条线段的和或差,分析这些线段的长度是已知的,还是要通过别的条件再求的,再进行逐段计算.
解:因为AB=4,BC=2AB,所以BC=8.
所以AC=AB+BC=4+8=12.
因为M 是线段AC 的中点,
所以MC=AM= AC=6.
所以BM=AM-AB=6-4=2.
如图4.3-11, 已知B,C 两点把线段AD 分成
2 ∶ 5 ∶ 3 三部分,点M 为AD 的中点,BM=6 cm,求CM 和AD 的长.
例4
解题秘方:利用已知条件BM=6 cm 作为等量关系列出方
程,求出CM 和AD 的长.
方法点拨
利用方程思想求线段的长的方法:
当利用逐段计算法难以求出线段长时,可考虑运用方程思想,将其中已知的线段长作为等量关系,设出要求的线段长,用含要求线段长的式子表示已知线段长(利用它们之间的数量关系表示),列出方程解决问题.
解:设AB=2x cm,则BC=5x cm,CD=3x cm.
所以AD=AB+BC+CD=10x cm.
因为M 是AD 的中点,
所以AM=MD= AD= ×10x=5x(cm).
因为BM=AM-AB,所以5x-2x=6. 所以x=2.
所以CM=MD-CD=5x-3x=2x=2×2=4(cm),
AD=10x=10×2=20(cm).
知识点
线段的基本事实
4
线段的基本事实 两点间的距离 举例
两点之间的所有连线中,线段最短. 简单说成:两点之间,线段最短 定义 性质
在所有连接A,B 两点的线中,线段AB 是最短的,线段AB 的长度就是点A与点B 之间的距离
两点之间线段的长度,叫做这两点之间的距离 (1)存在性; (2)最短性; (3)唯一性
警示误区
两点间的距离是一个具体的数量,而线段本身是图形. 因此不能把A,B 两点间的距离说成是线段AB. 另外, 连接两点是指画出以这两点端点的线段.
在同一所学校上学的小明、小亮、小红三位同学
分别住在A,B,C 三个住宅区,如图4.3-12,A,B,C 三点共线,且AB=40 m,BC=100 m,他们打算合租一辆车去上学. 由于车位紧张,他们准备在三个住宅区之间只设一个停靠点,为使三位同学步行到停靠点的路程之和最小,你认为停靠点应该设在何处?
例 5
解题秘方:根据停靠点的不同位置,分别计算他们步行
到停靠点的路程之和,再进行比较,确定位置.
技巧点拨
在解答某些数学问题时,有时会遇到多种情况,需要对各种情况加以分类,并逐类求解,然后综合得解,这就是分类讨论法,如本题中应分情况讨论车的停靠点.
解:AC=AB+BC=40+100=140(m).
分情况讨论如下:
(1)若停靠点设在A 住宅区,则他们的路程总和为
40+140=180(m);
(2)若停靠点设在A 住宅区与B 住宅区之间(不包括A,B 住宅区),则他们的路程总和大于140 m且小于180 m;
(3)若停靠点设在B 住宅区,则他们的路程总和为140 m;
(4)若停靠点设在B 住宅区与C 住宅区之间(不包括
B,C 住宅区),则他们的路程总和大于140 m且小于240 m;
(5)若停靠点设在C 住宅区,则他们的路程总和为
140+100=240(m).
综上所述,为使三位同学步行到停靠点的路程之和最小,
停靠点应设在B 住宅区.
详解
当停靠点位于A,B 之间时,不妨记为点D,如图4.3-13,则AD+DB=AB=40 m,100米=BC
你能画出来吗?
与你的同伴交流一下.
例6
解题秘方:蜘蛛要想最快地捉住虫子,需走最短的路线,
而蜘蛛走的路线在正方体的表面上,因此应在正方体
的表面展开图中寻找.
解: 有四种走法, 分别是B → F → A,B → G → A,
B → M → A,B → N → A(F,G,M,N 分别为DE,CD,
KE,KH 的中点),如图4.3-15.
线段、射线、直线
三线(线段、射线、直线)
直线的确定性
定义
表示方法
端点数
请完成教材课后习题
作业提升
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
