沪科版八年级数学上册 15.3.2 等腰三角形的判定 导学课件(共14张PPT)
文档属性
| 名称 | 沪科版八年级数学上册 15.3.2 等腰三角形的判定 导学课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 852.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 06:53:23 | ||
图片预览




文档简介
(共14张PPT)
15.3 等腰三角形
第15章 轴对称图形与等腰三角形
第2课时 等腰三角形的判定
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
等腰三角形的判定
知识点
等腰三角形的判定
感悟新知
1
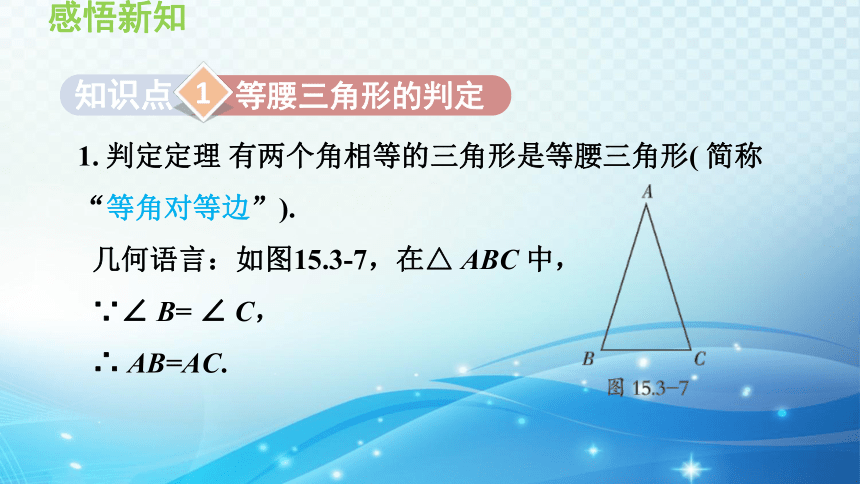
1. 判定定理 有两个角相等的三角形是等腰三角形( 简称“等角对等边”).
几何语言:如图15.3-7,在△ ABC 中,
∵∠ B= ∠ C,
∴ AB=AC.
感悟新知
特别提醒
“等角对等边”不能叙述为“ 如果一个三角形有两个底角相等,那么它的两条腰相等”, 因为在未判定出它是等腰三角形之前,不能用“底角”“顶角”“ 腰”“ 底边” 这些名词.
“等角对等边”是我们以后证明两条线段相等的常用方法,在证明过程中,经常通过计算三角形各角的度数,或利用角的关系得到角相等,从而得到所对的边相等.
2. 等腰三角形的性质与判定的异同
相同点:使用的前提都是“在同一个三角形中”.
不同点:由三角形的两边相等,得到它们所对的角相等,
是等腰三角形的性质;
由三角形的两角相等,得到它是等腰三角形,是等腰三角
形的判定.
即,等腰三角形的性质:两边相等→这两边所对的角相等.
等腰三角形的判定:两角相等→这两角所对的边相等.
感悟新知
感悟新知
例 1
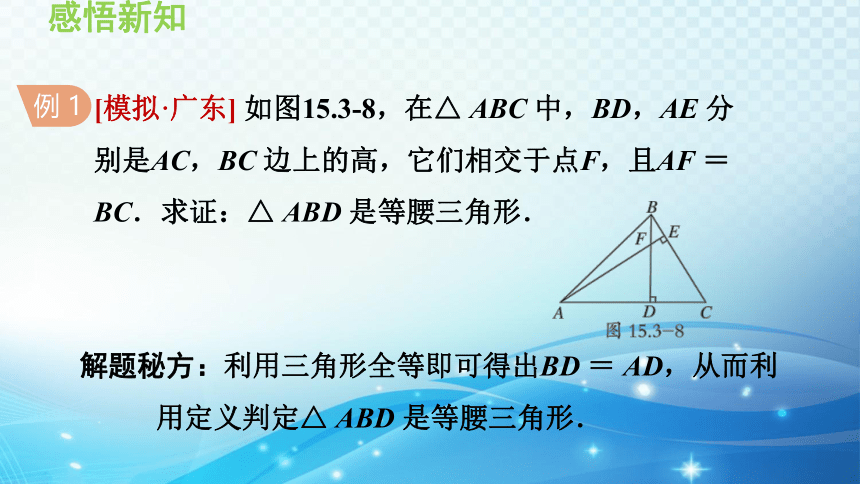
[模拟·广东] 如图15.3-8,在△ ABC 中,BD,AE 分
别是AC,BC 边上的高,它们相交于点F,且AF = BC.求证:△ ABD 是等腰三角形.
解题秘方:利用三角形全等即可得出BD = AD,从而利
用定义判定△ ABD 是等腰三角形.
感悟新知
解法提醒
掌握判定三角形是等腰三角形的两种方法是解题的关键:一是利用定义直接证明两条边相等;二是利用判定定理证明.
感悟新知
证明:∵ BD,AE 分别是AC,BC 边上的高,
∴ BD ⊥ AC,AE ⊥ BC,∴∠ BDC= ∠ ADF=90°,
∠ DBC+ ∠ BFE= ∠ DAF+ ∠ AFD=90° .
∵∠ BFE= ∠ AFD,∴∠ CBD= ∠ DAF.
在△ BCD 和△ AFD 中,∠ BDC= ∠ ADF,
∠ CBD= ∠ FAD,
BC=AF,
∴△ BCD ≌△ AFD,(AAS) ∴ BD=AD,
∴△ ABD 是等腰三角形.
感悟新知
例2
[期末·上海松江区] 如图15.3-9,已知在△ ABD 中,
AB=BD,∠ ADE= ∠ B.
求证:△ ADE 是等腰三角形.
解题秘方:根据等腰三角形的性质和
三角形的内角和定理可得∠ AED= ∠ BAD,利用等腰三角形的判定定理即可.
方法点拨
根据等腰三角形的判定定理可知,证明一个三角形是等腰三角形,就是要证明这个三角形有两个内角相等, 所以证明两个内角相等是判定等腰三角形的关键所在.
感悟新知
证明:∵ AB=BD,
∴∠ BAD= ∠ BDA.
∵∠ ADE= ∠ B,
∠ ADE+ ∠ BAD+ ∠ AED=180°,
∠ B+ ∠ BDA+ ∠ BAD=180°,
∴∠ AED= ∠ BAD,
∴ ED=AD,
∴△ ADE 是等腰三角形.
感悟新知
等腰三角形的判定
等腰三角形的三种判定方法:
(1)当三角形有两条边相等时,应用“有两条边相等的三
角形是等腰三角形”来证明.
(2)当三角形中有两个角相等时,应用“有两个角相等的
三角形是等腰三角形”来证明.
等腰三角形的判定
(3)当线段垂直平分线上的点与线段两端点构成三角形
时,应用“线段垂直平分线上的点到线段两端的距离
相等”来证明.
请完成教材课后习题
作业提升
15.3 等腰三角形
第15章 轴对称图形与等腰三角形
第2课时 等腰三角形的判定
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
等腰三角形的判定
知识点
等腰三角形的判定
感悟新知
1
1. 判定定理 有两个角相等的三角形是等腰三角形( 简称“等角对等边”).
几何语言:如图15.3-7,在△ ABC 中,
∵∠ B= ∠ C,
∴ AB=AC.
感悟新知
特别提醒
“等角对等边”不能叙述为“ 如果一个三角形有两个底角相等,那么它的两条腰相等”, 因为在未判定出它是等腰三角形之前,不能用“底角”“顶角”“ 腰”“ 底边” 这些名词.
“等角对等边”是我们以后证明两条线段相等的常用方法,在证明过程中,经常通过计算三角形各角的度数,或利用角的关系得到角相等,从而得到所对的边相等.
2. 等腰三角形的性质与判定的异同
相同点:使用的前提都是“在同一个三角形中”.
不同点:由三角形的两边相等,得到它们所对的角相等,
是等腰三角形的性质;
由三角形的两角相等,得到它是等腰三角形,是等腰三角
形的判定.
即,等腰三角形的性质:两边相等→这两边所对的角相等.
等腰三角形的判定:两角相等→这两角所对的边相等.
感悟新知
感悟新知
例 1
[模拟·广东] 如图15.3-8,在△ ABC 中,BD,AE 分
别是AC,BC 边上的高,它们相交于点F,且AF = BC.求证:△ ABD 是等腰三角形.
解题秘方:利用三角形全等即可得出BD = AD,从而利
用定义判定△ ABD 是等腰三角形.
感悟新知
解法提醒
掌握判定三角形是等腰三角形的两种方法是解题的关键:一是利用定义直接证明两条边相等;二是利用判定定理证明.
感悟新知
证明:∵ BD,AE 分别是AC,BC 边上的高,
∴ BD ⊥ AC,AE ⊥ BC,∴∠ BDC= ∠ ADF=90°,
∠ DBC+ ∠ BFE= ∠ DAF+ ∠ AFD=90° .
∵∠ BFE= ∠ AFD,∴∠ CBD= ∠ DAF.
在△ BCD 和△ AFD 中,∠ BDC= ∠ ADF,
∠ CBD= ∠ FAD,
BC=AF,
∴△ BCD ≌△ AFD,(AAS) ∴ BD=AD,
∴△ ABD 是等腰三角形.
感悟新知
例2
[期末·上海松江区] 如图15.3-9,已知在△ ABD 中,
AB=BD,∠ ADE= ∠ B.
求证:△ ADE 是等腰三角形.
解题秘方:根据等腰三角形的性质和
三角形的内角和定理可得∠ AED= ∠ BAD,利用等腰三角形的判定定理即可.
方法点拨
根据等腰三角形的判定定理可知,证明一个三角形是等腰三角形,就是要证明这个三角形有两个内角相等, 所以证明两个内角相等是判定等腰三角形的关键所在.
感悟新知
证明:∵ AB=BD,
∴∠ BAD= ∠ BDA.
∵∠ ADE= ∠ B,
∠ ADE+ ∠ BAD+ ∠ AED=180°,
∠ B+ ∠ BDA+ ∠ BAD=180°,
∴∠ AED= ∠ BAD,
∴ ED=AD,
∴△ ADE 是等腰三角形.
感悟新知
等腰三角形的判定
等腰三角形的三种判定方法:
(1)当三角形有两条边相等时,应用“有两条边相等的三
角形是等腰三角形”来证明.
(2)当三角形中有两个角相等时,应用“有两个角相等的
三角形是等腰三角形”来证明.
等腰三角形的判定
(3)当线段垂直平分线上的点与线段两端点构成三角形
时,应用“线段垂直平分线上的点到线段两端的距离
相等”来证明.
请完成教材课后习题
作业提升
