沪科版八年级上册15.4.2 角的平分线的判定 课件(共16张PPT)
文档属性
| 名称 | 沪科版八年级上册15.4.2 角的平分线的判定 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 920.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 08:01:29 | ||
图片预览






文档简介
(共16张PPT)
15.4 等腰三角形
第15章 轴对称图形与等腰三角形
第2课时 角的平分线的判定
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
角的平分线的判定
三角形的角平分线的性质(拓展点)
知识点
角的平分线的判定
感悟新知
1
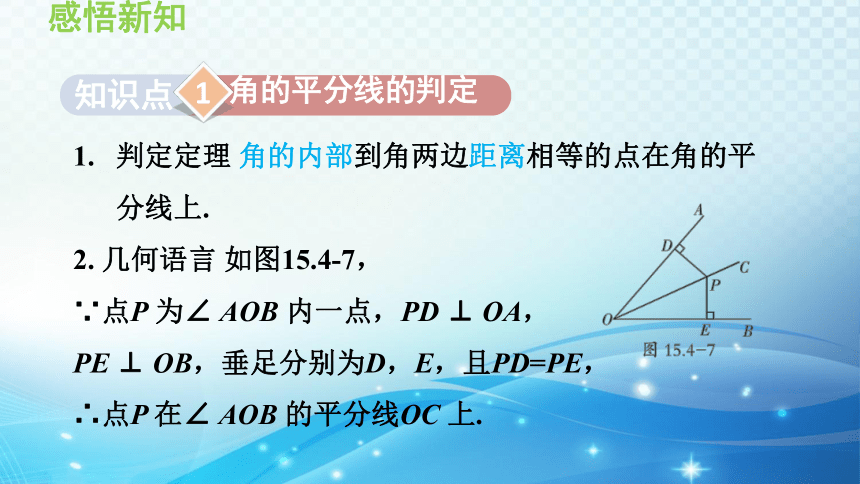
判定定理 角的内部到角两边距离相等的点在角的平分线上.
2. 几何语言 如图15.4-7,
∵点P 为∠ AOB 内一点,PD ⊥ OA,
PE ⊥ OB,垂足分别为D,E,且PD=PE,
∴点P 在∠ AOB 的平分线OC 上.
感悟新知
特别提醒
1. 使用该判定定理的前提是这个点必须在角的内部.
2. 角的平分线的判定是由两个条件(垂线,线段相等)
得到一个结论(角平分线).
3. 角的平分线的判定定理是证明两角相等的重要依据,
它比利用三角形全等证两角相等更方便快捷.
感悟新知
3. 角平分线的判定定理与性质定理的关系
(1)如图15.4-7,都与距离有关:即条件PD ⊥ OA,
PE ⊥ OB 都具备;
(2)点在角的平分线上 (角的内部的)点到角两边
的距离相等.
性质
判定
感悟新知
例 1
[月考·大连] 如图15.4-8,在△ ABC 中,D 是BC 的中点,DE ⊥ AB,DF ⊥ AC,垂足分别是E,F,BE = CF.
求证:AD 是△ ABC 的角平分线.
解题秘方:首先利用三角形全等得出
DE=DF,再根据三角形角平分线的判定定理即可求证.
感悟新知
方法点拨
证明角平分线的方法思路:
1. 从数量上证明被角平分线分成的两个角相等.
2. 从形上证明角的内部的点到角两边的距离相等,即只需从要证的线上的某一点向角的两边作垂线段,再证明垂线段相等即可.这样把“某线是角的平分线”的问题转化为证“垂线段相等”的问题,体现了转化思想.
感悟新知
证明:∵ DE ⊥ AB,DF ⊥ AC,
∴△ BDE 和△ CDF 是直角三角形.
∵ BD=DC,
BE=CF,
∴ Rt △ BDE ≌ Rt △ CDF,(HL)∴ DE = DF.
∵ DE ⊥ AB,DF ⊥ AC,DE = DF,
∴点D 在∠ BAC 的平分线上,即AD 是△ ABC 的角平分线.
知识点
三角形的角平分线的性质(拓展点)
感悟新知
2
性质定理 三角形三条内角平分线相交于一点,这点到三角形三边的距离相等. 这一点叫三角形的内心.
要点解读
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等. 反之,三角形内部到三边距离
相等的点是三角形三条角平分线的交点.
感悟新知
2. 几何语言
如图15.4-9,在△ ABC 中,AD,BM,CN 分别是∠ BAC,∠ ABC,∠ ACB 的平分线,AD,BM,CN 交于一点O,且点O 到三边BC,AB,AC 的距离(OE,OG,OF 的长)相等,即OE=OG=OF.
感悟新知
例2
[月考·滨州]如图15.4-10,点P 为∠ ABC 和∠ MAC
的平分线的交点.求证:点P 在∠ ACN 的平分线上.
解题秘方:紧扣到CA,CN 的距离相等的点在该角的平分线上.
方法点拨
角平分线的性质与判定都离不开“点到角两边的距离”, 所以过点作角两边的垂线是运用角平分线性质或判定最常见的辅助线. 因此常将证角平分线转化为证垂线段相等;反之也常将证垂线段相等转化为证角平分线.
感悟新知
证明:过P 作PE ⊥ BM 于E,PF ⊥ AC 于F,PG ⊥ BN
于G,∵ P 为∠ ABC 和∠ MAC 的平分线的交点,
∴ PE = PF,PE = PG,
∴ PF = PG,
∴点P 在∠ ACN 的平分线上.
感悟新知
角的平分线的判定
角的平分线的性质与判定定理的关系:
(1)都与距离有关,即垂直的条件都应具备.
(2)点在角的平分线上 点到这个角两边的距离相
等.
性质
判定定理
角的平分线的判定
(3)性质反映的是只要是角的平分线上的点,到角两边的
距离就一定相等;判定定理反映的是只要是角的内部
到角两边距离相等的点都在角的平分线上.
请完成教材课后习题
作业提升
15.4 等腰三角形
第15章 轴对称图形与等腰三角形
第2课时 角的平分线的判定
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
角的平分线的判定
三角形的角平分线的性质(拓展点)
知识点
角的平分线的判定
感悟新知
1
判定定理 角的内部到角两边距离相等的点在角的平分线上.
2. 几何语言 如图15.4-7,
∵点P 为∠ AOB 内一点,PD ⊥ OA,
PE ⊥ OB,垂足分别为D,E,且PD=PE,
∴点P 在∠ AOB 的平分线OC 上.
感悟新知
特别提醒
1. 使用该判定定理的前提是这个点必须在角的内部.
2. 角的平分线的判定是由两个条件(垂线,线段相等)
得到一个结论(角平分线).
3. 角的平分线的判定定理是证明两角相等的重要依据,
它比利用三角形全等证两角相等更方便快捷.
感悟新知
3. 角平分线的判定定理与性质定理的关系
(1)如图15.4-7,都与距离有关:即条件PD ⊥ OA,
PE ⊥ OB 都具备;
(2)点在角的平分线上 (角的内部的)点到角两边
的距离相等.
性质
判定
感悟新知
例 1
[月考·大连] 如图15.4-8,在△ ABC 中,D 是BC 的中点,DE ⊥ AB,DF ⊥ AC,垂足分别是E,F,BE = CF.
求证:AD 是△ ABC 的角平分线.
解题秘方:首先利用三角形全等得出
DE=DF,再根据三角形角平分线的判定定理即可求证.
感悟新知
方法点拨
证明角平分线的方法思路:
1. 从数量上证明被角平分线分成的两个角相等.
2. 从形上证明角的内部的点到角两边的距离相等,即只需从要证的线上的某一点向角的两边作垂线段,再证明垂线段相等即可.这样把“某线是角的平分线”的问题转化为证“垂线段相等”的问题,体现了转化思想.
感悟新知
证明:∵ DE ⊥ AB,DF ⊥ AC,
∴△ BDE 和△ CDF 是直角三角形.
∵ BD=DC,
BE=CF,
∴ Rt △ BDE ≌ Rt △ CDF,(HL)∴ DE = DF.
∵ DE ⊥ AB,DF ⊥ AC,DE = DF,
∴点D 在∠ BAC 的平分线上,即AD 是△ ABC 的角平分线.
知识点
三角形的角平分线的性质(拓展点)
感悟新知
2
性质定理 三角形三条内角平分线相交于一点,这点到三角形三边的距离相等. 这一点叫三角形的内心.
要点解读
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等. 反之,三角形内部到三边距离
相等的点是三角形三条角平分线的交点.
感悟新知
2. 几何语言
如图15.4-9,在△ ABC 中,AD,BM,CN 分别是∠ BAC,∠ ABC,∠ ACB 的平分线,AD,BM,CN 交于一点O,且点O 到三边BC,AB,AC 的距离(OE,OG,OF 的长)相等,即OE=OG=OF.
感悟新知
例2
[月考·滨州]如图15.4-10,点P 为∠ ABC 和∠ MAC
的平分线的交点.求证:点P 在∠ ACN 的平分线上.
解题秘方:紧扣到CA,CN 的距离相等的点在该角的平分线上.
方法点拨
角平分线的性质与判定都离不开“点到角两边的距离”, 所以过点作角两边的垂线是运用角平分线性质或判定最常见的辅助线. 因此常将证角平分线转化为证垂线段相等;反之也常将证垂线段相等转化为证角平分线.
感悟新知
证明:过P 作PE ⊥ BM 于E,PF ⊥ AC 于F,PG ⊥ BN
于G,∵ P 为∠ ABC 和∠ MAC 的平分线的交点,
∴ PE = PF,PE = PG,
∴ PF = PG,
∴点P 在∠ ACN 的平分线上.
感悟新知
角的平分线的判定
角的平分线的性质与判定定理的关系:
(1)都与距离有关,即垂直的条件都应具备.
(2)点在角的平分线上 点到这个角两边的距离相
等.
性质
判定定理
角的平分线的判定
(3)性质反映的是只要是角的平分线上的点,到角两边的
距离就一定相等;判定定理反映的是只要是角的内部
到角两边距离相等的点都在角的平分线上.
请完成教材课后习题
作业提升
