沪科版八年级上册15.2 线段的垂直平分线 课件(共24张PPT)
文档属性
| 名称 | 沪科版八年级上册15.2 线段的垂直平分线 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 08:05:25 | ||
图片预览






文档简介
(共24张PPT)
15.2 线段的垂直平分线
第15章 轴对称图形与等腰三角形
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
线段的垂直平分线的作法
线段垂直平分线的性质
线段垂直平分线的判定
知识点
线段的垂直平分线的作法
感悟新知
1
1. 作线段的垂直平分线的常用方法
(1)折纸:在半透明纸上画一条线段AA′, 折纸, 使A 与A′重合,得到的折痕l 是线段AA′的垂直平分线.
(2)过中点画垂线:先用刻度尺量出线段的中点,再用三角尺过中点画垂线,所得的垂线即为线段的垂直平分线.
(3)尺规作图:保留作图痕迹,并指出结论.
感悟新知
特别解读
作法中,“ 大于 AB 长为半径画弧”才能确保有两个交点,这个半径不能“等于或小于 AB 长”,要明确这一点.
感悟新知
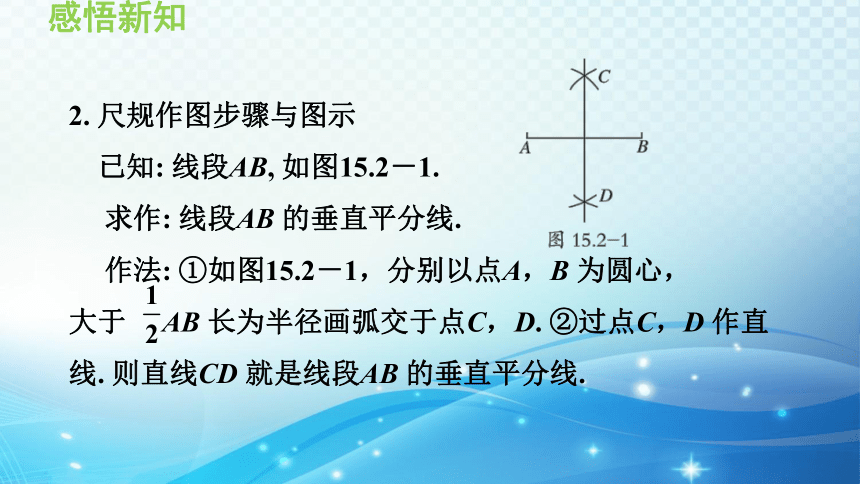
2. 尺规作图步骤与图示
已知: 线段AB, 如图15.2-1.
求作: 线段AB 的垂直平分线.
作法: ①如图15.2-1,分别以点A,B 为圆心,
大于 AB 长为半径画弧交于点C,D. ②过点C,D 作直线. 则直线CD 就是线段AB 的垂直平分线.
感悟新知
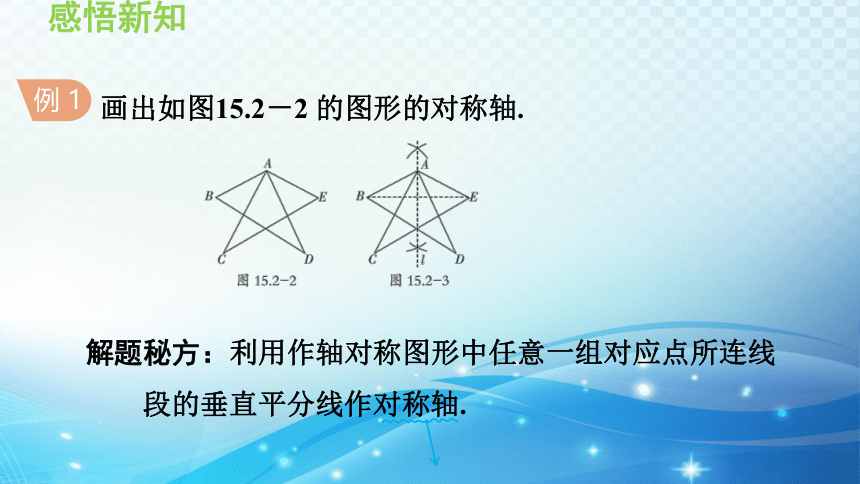
例 1
画出如图15.2-2 的图形的对称轴.
解题秘方:利用作轴对称图形中任意一组对应点所连线
段的垂直平分线作对称轴.
感悟新知
方法点拨
作轴对称图形的对称轴的两种方法:
一是折叠法,将轴对称图形对折,折痕所在的直线为对称轴;
二是先找到轴对称图形的一组对应点,再作连接这组对应点的线段的垂直平分线.
感悟新知
解:作法:如图15.2-3.
(1)连接BE;
(2)作线段BE 的垂直平分线l,则直线l 即为所求作的
对称轴.
线段垂直平分线的性质
感悟新知
知识点
2
1. 性质 线段垂直平分线上的点到线段两端的距离相等.
条件:点在线段的垂直平分线上.
结论:这个点到线段两端点的距离相等.
2. 几何语言 如图15.2-4,
∵ AD ⊥ BC,BD=CD,
∴ AB=AC.
感悟新知
特别解读
1. 线段的垂直平分线的性质中的“距离”是“点与 这条线段两个端点的距离”.
2. 用线段的垂直平分线的性质可直接证明线
段相等,不必再用三角形全等来证明,因此它为证明线段相等提供了新方法.
感悟新知
例2
[期末·宝鸡金台区]如图15.2-5, △ ABC 中,DE,
FG 分别为AB,AC 的垂直平分线,E,G 分别为垂足,∠ DAF=20°.
(1)若△ DAF 的周长为6,求BC 的长;
(2)求∠ BAC 的度数.
感悟新知
解题秘方:(1)根据线段垂直平分线的性质得到DA=DB,FA=FC,根据三角形的周长公式计算即可;
(2)根据全等三角形对应角相等可得到∠ DAB= ∠ B,∠ FAC= ∠ C,根据三角形内角和定理计算,得到答案.
感悟新知
解法指导
利用线段的垂直平分线的性质转化线段的位置,是一种常用的解题方法. 本题中解题的关键是利用线段垂直平分线的性质将BC 的长转化为△ DAF 的周长, 进行求解.
感悟新知
解:(1)∵△ DAF 的周长为6,
∴ DA+FA+DF=6.
∵ DE,FG 分别为AB,AC 的垂直平分线,
∴ DA=DB,FA=FC,
∴ BC=DB+DF+FC=DA+DF+FA=6.
感悟新知
(2)∵ DA=DB,EA=EB,DE=DE,
∴△ DAE ≌△ DBE, ∴∠ DAB =∠ B,
同理:∠ FAC= ∠ C, ∴∠ DAB+ ∠ FAC= ∠ B+ ∠ C.
∵∠ DAF=20°,
∴∠ DAB+ ∠ FAC+ ∠ B+ ∠ C
=180° -20° =160°,
∴∠ DAB+ ∠ FAC=80°,
∴∠ BAC=80° +20° =100°.
感悟新知
1. 判定 到线段两端距离相等的点在线段的垂直平分线上.
条件:点到线段两个端点距离相等.
结论:点在线段的垂直平分线上.
线段垂直平分线的判定
知识点
3
特别解读
1. 证明一个点在一条线段的垂直平分线上,思路有两种:一是作垂直, 证平分.二是取中点证垂直.
2. 证明线段的垂直平分线,必须证明两个点在垂直平分线上.
感悟新知
2. 几何语言 如图15.2-6,
∵ AB=AC,
∴点A 在线段BC 的垂直平分线上.
3. 三角形三边的垂直平分线的性质 三
角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等.
感悟新知
例 3
如图15.2-7,AD 为∠ BAC 的平分线,交BC 于点D,
AE=AF,请判断线段AD 所在的直线是否为线段EF 的垂直平分线,若是,请给予证明;若不是,请说明理由.
感悟新知
解题秘方:紧扣线段的垂直平分线的判定证明直线AD 上的点A 和点D 到线段EF 的两个端点的距离相等即可.
感悟新知
教你一招
判断线段垂直平分线的两种方法:
一是定义法,
二是判定定理. 一般习惯用定义法进行判断, 而利用判定定理判断更简单. 用判定定理判定一条直线是线段的垂直平分线时,一定要证明直线上有两点到线段两个端点的距离相等.
解 :线段AD 所在的直线是线段EF 的垂直平分线. 证明如下:如图15.2-7,连接DE,DF.
∵ AD 是∠ BAC 的平分线,∴∠ EAD= ∠ FAD.
在△ AED 和△ AFD 中,
AE=AF,
∠ EAD= ∠ FAD,
AD=AD,
∴△ AED ≌△ AFD.(SAS)
感悟新知
∴ DE=DF.
∴点D 在线段EF 的垂直平分线上.
∵ AE=AF,
∴点A 在线段EF 的垂直平分线上.
∴线段AD 所在的直线是线段EF 的垂直平分线.
感悟新知
切忌只证明一个点在直线上,就说过该点的直线是线段的垂直平分线.
线段的垂直平分线
线段的垂直平分线
性质
作线段的垂直平分线
判定
尺规作画
请完成教材课后习题
作业提升
15.2 线段的垂直平分线
第15章 轴对称图形与等腰三角形
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
线段的垂直平分线的作法
线段垂直平分线的性质
线段垂直平分线的判定
知识点
线段的垂直平分线的作法
感悟新知
1
1. 作线段的垂直平分线的常用方法
(1)折纸:在半透明纸上画一条线段AA′, 折纸, 使A 与A′重合,得到的折痕l 是线段AA′的垂直平分线.
(2)过中点画垂线:先用刻度尺量出线段的中点,再用三角尺过中点画垂线,所得的垂线即为线段的垂直平分线.
(3)尺规作图:保留作图痕迹,并指出结论.
感悟新知
特别解读
作法中,“ 大于 AB 长为半径画弧”才能确保有两个交点,这个半径不能“等于或小于 AB 长”,要明确这一点.
感悟新知
2. 尺规作图步骤与图示
已知: 线段AB, 如图15.2-1.
求作: 线段AB 的垂直平分线.
作法: ①如图15.2-1,分别以点A,B 为圆心,
大于 AB 长为半径画弧交于点C,D. ②过点C,D 作直线. 则直线CD 就是线段AB 的垂直平分线.
感悟新知
例 1
画出如图15.2-2 的图形的对称轴.
解题秘方:利用作轴对称图形中任意一组对应点所连线
段的垂直平分线作对称轴.
感悟新知
方法点拨
作轴对称图形的对称轴的两种方法:
一是折叠法,将轴对称图形对折,折痕所在的直线为对称轴;
二是先找到轴对称图形的一组对应点,再作连接这组对应点的线段的垂直平分线.
感悟新知
解:作法:如图15.2-3.
(1)连接BE;
(2)作线段BE 的垂直平分线l,则直线l 即为所求作的
对称轴.
线段垂直平分线的性质
感悟新知
知识点
2
1. 性质 线段垂直平分线上的点到线段两端的距离相等.
条件:点在线段的垂直平分线上.
结论:这个点到线段两端点的距离相等.
2. 几何语言 如图15.2-4,
∵ AD ⊥ BC,BD=CD,
∴ AB=AC.
感悟新知
特别解读
1. 线段的垂直平分线的性质中的“距离”是“点与 这条线段两个端点的距离”.
2. 用线段的垂直平分线的性质可直接证明线
段相等,不必再用三角形全等来证明,因此它为证明线段相等提供了新方法.
感悟新知
例2
[期末·宝鸡金台区]如图15.2-5, △ ABC 中,DE,
FG 分别为AB,AC 的垂直平分线,E,G 分别为垂足,∠ DAF=20°.
(1)若△ DAF 的周长为6,求BC 的长;
(2)求∠ BAC 的度数.
感悟新知
解题秘方:(1)根据线段垂直平分线的性质得到DA=DB,FA=FC,根据三角形的周长公式计算即可;
(2)根据全等三角形对应角相等可得到∠ DAB= ∠ B,∠ FAC= ∠ C,根据三角形内角和定理计算,得到答案.
感悟新知
解法指导
利用线段的垂直平分线的性质转化线段的位置,是一种常用的解题方法. 本题中解题的关键是利用线段垂直平分线的性质将BC 的长转化为△ DAF 的周长, 进行求解.
感悟新知
解:(1)∵△ DAF 的周长为6,
∴ DA+FA+DF=6.
∵ DE,FG 分别为AB,AC 的垂直平分线,
∴ DA=DB,FA=FC,
∴ BC=DB+DF+FC=DA+DF+FA=6.
感悟新知
(2)∵ DA=DB,EA=EB,DE=DE,
∴△ DAE ≌△ DBE, ∴∠ DAB =∠ B,
同理:∠ FAC= ∠ C, ∴∠ DAB+ ∠ FAC= ∠ B+ ∠ C.
∵∠ DAF=20°,
∴∠ DAB+ ∠ FAC+ ∠ B+ ∠ C
=180° -20° =160°,
∴∠ DAB+ ∠ FAC=80°,
∴∠ BAC=80° +20° =100°.
感悟新知
1. 判定 到线段两端距离相等的点在线段的垂直平分线上.
条件:点到线段两个端点距离相等.
结论:点在线段的垂直平分线上.
线段垂直平分线的判定
知识点
3
特别解读
1. 证明一个点在一条线段的垂直平分线上,思路有两种:一是作垂直, 证平分.二是取中点证垂直.
2. 证明线段的垂直平分线,必须证明两个点在垂直平分线上.
感悟新知
2. 几何语言 如图15.2-6,
∵ AB=AC,
∴点A 在线段BC 的垂直平分线上.
3. 三角形三边的垂直平分线的性质 三
角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等.
感悟新知
例 3
如图15.2-7,AD 为∠ BAC 的平分线,交BC 于点D,
AE=AF,请判断线段AD 所在的直线是否为线段EF 的垂直平分线,若是,请给予证明;若不是,请说明理由.
感悟新知
解题秘方:紧扣线段的垂直平分线的判定证明直线AD 上的点A 和点D 到线段EF 的两个端点的距离相等即可.
感悟新知
教你一招
判断线段垂直平分线的两种方法:
一是定义法,
二是判定定理. 一般习惯用定义法进行判断, 而利用判定定理判断更简单. 用判定定理判定一条直线是线段的垂直平分线时,一定要证明直线上有两点到线段两个端点的距离相等.
解 :线段AD 所在的直线是线段EF 的垂直平分线. 证明如下:如图15.2-7,连接DE,DF.
∵ AD 是∠ BAC 的平分线,∴∠ EAD= ∠ FAD.
在△ AED 和△ AFD 中,
AE=AF,
∠ EAD= ∠ FAD,
AD=AD,
∴△ AED ≌△ AFD.(SAS)
感悟新知
∴ DE=DF.
∴点D 在线段EF 的垂直平分线上.
∵ AE=AF,
∴点A 在线段EF 的垂直平分线上.
∴线段AD 所在的直线是线段EF 的垂直平分线.
感悟新知
切忌只证明一个点在直线上,就说过该点的直线是线段的垂直平分线.
线段的垂直平分线
线段的垂直平分线
性质
作线段的垂直平分线
判定
尺规作画
请完成教材课后习题
作业提升
