沪科版八年级上册15.1.1 轴对称 课件(共32张PPT)
文档属性
| 名称 | 沪科版八年级上册15.1.1 轴对称 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 08:08:06 | ||
图片预览









文档简介
(共32张PPT)
15.1 轴对称图形
第15章 轴对称图形与等腰三角形
第1课时 轴对称
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
轴对称图形
轴对称
线段的垂直平分线
轴对称的性质
知识点
轴对称图形
感悟新知
1
1. 定义 如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴. 我们也说这个图形关于这条直线(成轴)对称.
特别解读
轴对称图形的三个条件:
1. 一个整体图形;2. 一条直线:对称轴;
3. 直线两旁的部分完全重合.
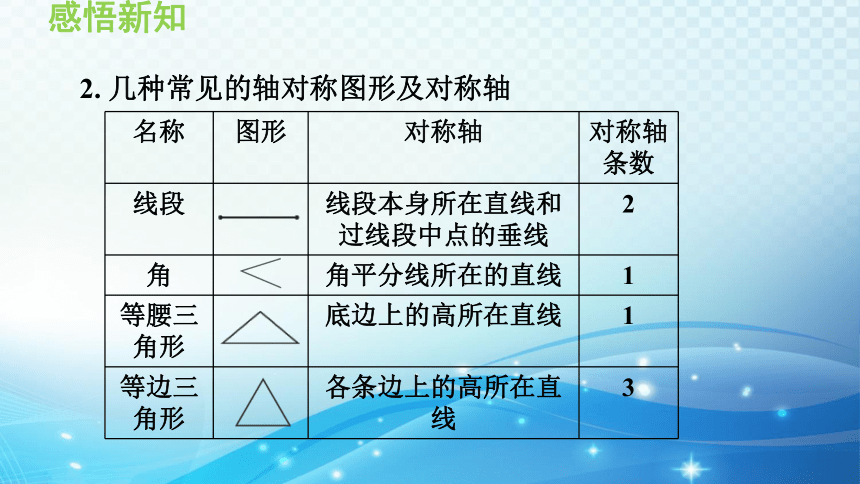
2. 几种常见的轴对称图形及对称轴
感悟新知
名称 图形 对称轴 对称轴条数
线段 线段本身所在直线和过线段中点的垂线 2
角 角平分线所在的直线 1
等腰三角形 底边上的高所在直线 1
等边三角形 各条边上的高所在直线 3
感悟新知
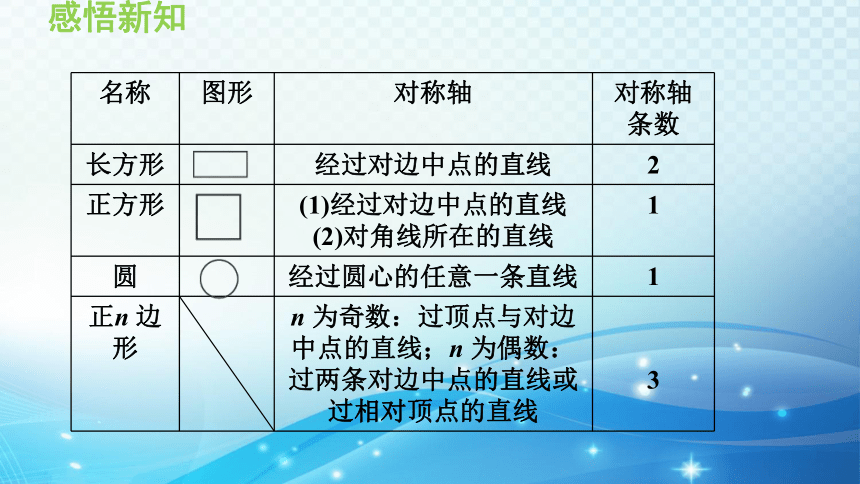
名称 图形 对称轴 对称轴条数
长方形 经过对边中点的直线 2
正方形 (1)经过对边中点的直线
(2)对角线所在的直线 1
圆 经过圆心的任意一条直线 1
正n 边形 n 为奇数:过顶点与对边中点的直线;n 为偶数:过两条对边中点的直线或过相对顶点的直线
3
感悟新知
温馨提示
1. 轴对称图形是一个图形自身的特性,它被对称轴分 成的两部分能够互相重合,其对称点在同一图形上.
2. 对称轴是一条直线,而不是射线或线段.
3. 一个轴对称图形的对称轴可以有1 条,也可以有多条,还可以有无数条.
感悟新知
例 1
下面是组成北京2022 年冬奥会会徽的四个图案,其
中是轴对称图形的是( )
A. B. C. D.
解题秘方:根据轴对称图形的概念对各选项分析判断.
感悟新知
解:A.不是轴对称图形,故本选项不合题意;
B.不是轴对称图形,故本选项不合题意;
C.不是轴对称图形,故本选项不合题意;
D.是轴对称图形,故本选项符合题意.
答案:D
方法点拨:识别轴对称图形的关键是寻找到对称轴,若
图形两部分折叠后可重合,即可确定这个图形是轴对称图形,否则就不是轴对称图形.
轴对称
感悟新知
知识点
2
1. 定义
平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴. 折叠后重合的两点叫做对应点(也叫对称点).
感悟新知
特别解读
轴对称的三个条件:
1. 有两个图形;
2. 存在一条直线;
3. 一个图形沿着这条直线折叠后与另一个图形重合.
轴对称的两个特性:
1. 成轴对称的两个图形全等. 但全等的两个图形不一定成轴对称.
2. 轴对称是图形的一种全等变换.
感悟新知
2. 轴对称与轴对称图形的区别与联系
名称 轴对称 轴对称图形
区别 对象不同 两个图形 一个图形
意义不同 两个图形的特殊位置关系 一个具有特殊形状的图形
对称点位置不同 对称点分别在两个图形上 轴对称图形的对称轴一定经过这个图形的内部
对称轴位置不同 两个图形成轴对称,其对称轴可能在两个图形的外部,也可能经过两个图形的内部或它们的公共边(点) 轴对称图形的对称轴一定经过这个图形的内部
感悟新知
名称 轴对称 轴对称图形
区别 对称轴数量不同 只有一条对称轴 有一条或多条
联系 (1)定义中都有一条直线,都要沿着这条直线折叠
(2)把成轴对称的两个图形看成一个整体,它就是一个轴对称图形. 把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称
感悟新知
例2
[期末·北京朝阳区]如图15.1-1 下面镜子里哪个是他的像?( )
A. ① B. ② C. ③ D. ④
感悟新知
解题秘方:镜面对称的实质就是把平面镜看成对称轴,
若平面镜两旁的图形能对称,则根据定义就可得出答案.
感悟新知
方法点拨
镜面对称的本质就是以平面镜为对称轴的轴对称,而识别轴对称的方法:
1. 定义法:紧扣定义中的“两个图形,一条直线,完全重合”.
2. 反面观察法:从纸的反面观察图形,若观察到的和正面一样,就是轴对称.
感悟新知
解:由轴对称的性质,连接对应点的线段与镜面垂直并
且被镜面平分,即可得出只有②与原图形成镜面对称.
答案:B
感悟新知
1. 定义 经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线,又叫做线段的中垂线.
线段的垂直平分线
知识点
3
特别解读
1. 线段的垂直平分线必须满足两个条件:
(1) 经过线段的中点;
(2) 垂直于这条线段. 两者缺一不可.
2. 线段的垂直平分线的定义反过来也成立.
感悟新知
2. 几何语言 如图15.1-2,
∵ DC ⊥ AB,AC=BC,
∴ DC 是AB 的垂直平分线.
反过来也成立:
∵ DC 是AB 的垂直平分线,
∴ DC ⊥ AB,AC=BC.
感悟新知
例 3
如图15.1-3,直线AE 是线段BC 的垂直平分线,垂足为E,D 是直线AE 上任意一点,
求证:∠ ABD= ∠ ACD.
感悟新知
解法提醒
1.由直线AE 是线段BC 的垂直平分线得出BE=CE,AE ⊥ BC. 这两个结论有时根据证题需要可只写出其中一
个结论.
2.若要证AE 是线段BC 的垂直平分线,则必须同时具备BE=CE,AE⊥ BC 这两个条件.
解题秘方:紧扣线段的垂直平分线的定义进行解答.
证明:∵直线AE 是线段BC 的垂直平分线,
∴ BE=CE,AE ⊥ BC. ∴∠ AEB= ∠ AEC=90° .
在Rt △ ABE 和Rt △ ACE 中, AE=AE,
∠ AEB= ∠ AEC,
BE=CE,
∴ Rt △ ABE ≌ Rt △ ACE.(SAS)
∴∠ ABE= ∠ ACE. 同理可证∠ DBE= ∠ DCE,
∴∠ ABE - ∠ DBE= ∠ ACE- ∠ DCE,即∠ ABD= ∠ ACD.
感悟新知
感悟新知
1. 轴对称的性质 如果两个图形关于某直线对
称,那么对称轴是任何一对对应点所连线
段的垂直平分线,如图15.1-4.
特别地:成轴对称的两个图形的对应
线段所在直线平行或者重合或者相交于某
一点,且该点一定在对称轴上.
2. 反之 成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
轴对称的性质
知识点
4
感悟新知
特别解读
轴对称图形或成轴对称的两个图形的对应线段、对
应角相等;
2. 轴对称图形被对称轴分成的两部分全等,并且这两部分关于对称轴成轴对称. 成轴对称的两个图形也全等,但全等的两个图形不一定成轴对称.
感悟新知
[模拟·深圳]如图15.1-5,在△ ABC 中,点D,E
分别在边AB,BC 上, 点A 与点E 关于直线CD 对称. 若AB=7,AC=9,BC=12,则△ DBE 的周长为( )
A.9 B.10
C.11 D.12
例4
感悟新知
解法提醒
轴对称的性质中关键有两点:
一是对应图形的全等性,根据全等的性质可得到对应的边、角相等;
二是对称轴的垂直平分性. 揭示对称轴与对应点所连线段之间的位置关系.
解题秘方:根据轴对称的性质得到:AD=DE,AC=CE, 结合已知条件和三角形周长公式解答.
解:∵点A 与点E 关于直线CD 对称,
∴ AD=DE,AC=CE = 9.
∵ AB=7,AC=9,BC=12,
∴△ DBE 的周长=BD+DE+BE
=BD+AD+BC-AC
=AB+BC-AC
=7+12-9=10.
答案:B
感悟新知
感悟新知
例 5
如图15.1-6, △ ABC 中,D,E,F 三点分别在
AB,BC,AC 上,且四边形BEFD 是以DE 为对称轴的轴对称图形,四边形CFDE 是以FE 为对称轴的轴对称图形.若∠ C=40°,则∠ DFE 的度数为( )
A.65° B.70°
C.75° D.80°
感悟新知
解题秘方:根据轴对称的性质可得∠ BED= ∠ DEF=
∠ CEF,据此可得∠ DEF=60°,∠ EDF= ∠C=40°,再根据三角形的内角和定理可得
∠ DFE 的度数.
感悟新知
解法提醒
利用轴对称的性质求线段的长度或角的度数的方法:
先根据成轴对称的特征确定两个图形的对应边、对应角,再运用轴对称的性质(对应边相等,对应角相等),把要求的边或角与已知的对应边或对应角建立联系,从而求出待求的线段的长度或角的度数.
感悟新知
解:∵四边形BEFD 是以DE 为对称轴的轴对称图形,四
边形CFDE 是以FE 为对称轴的轴对称图形,
∴∠ BED= ∠ DEF= ∠ CEF= ,
∠ EDF= ∠ C=40°,
∴∠ DFE=180° - ∠ DEF- ∠ EDF=80° .
答案:D
轴对称图形
轴对称和轴对称图形的区别:
(1)定义不同;
(2)轴对称图形指的是一个图形,而两个图形成轴
对称指的是两个图形;
(3)一个轴对称图形的对称轴可能有多条,而两个
图形成轴对称的对称轴一般只有一条.
请完成教材课后习题
作业提升
15.1 轴对称图形
第15章 轴对称图形与等腰三角形
第1课时 轴对称
逐点
学练
本节小结
作业提升
学习目标
本节要点
1
学习流程
2
轴对称图形
轴对称
线段的垂直平分线
轴对称的性质
知识点
轴对称图形
感悟新知
1
1. 定义 如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴. 我们也说这个图形关于这条直线(成轴)对称.
特别解读
轴对称图形的三个条件:
1. 一个整体图形;2. 一条直线:对称轴;
3. 直线两旁的部分完全重合.
2. 几种常见的轴对称图形及对称轴
感悟新知
名称 图形 对称轴 对称轴条数
线段 线段本身所在直线和过线段中点的垂线 2
角 角平分线所在的直线 1
等腰三角形 底边上的高所在直线 1
等边三角形 各条边上的高所在直线 3
感悟新知
名称 图形 对称轴 对称轴条数
长方形 经过对边中点的直线 2
正方形 (1)经过对边中点的直线
(2)对角线所在的直线 1
圆 经过圆心的任意一条直线 1
正n 边形 n 为奇数:过顶点与对边中点的直线;n 为偶数:过两条对边中点的直线或过相对顶点的直线
3
感悟新知
温馨提示
1. 轴对称图形是一个图形自身的特性,它被对称轴分 成的两部分能够互相重合,其对称点在同一图形上.
2. 对称轴是一条直线,而不是射线或线段.
3. 一个轴对称图形的对称轴可以有1 条,也可以有多条,还可以有无数条.
感悟新知
例 1
下面是组成北京2022 年冬奥会会徽的四个图案,其
中是轴对称图形的是( )
A. B. C. D.
解题秘方:根据轴对称图形的概念对各选项分析判断.
感悟新知
解:A.不是轴对称图形,故本选项不合题意;
B.不是轴对称图形,故本选项不合题意;
C.不是轴对称图形,故本选项不合题意;
D.是轴对称图形,故本选项符合题意.
答案:D
方法点拨:识别轴对称图形的关键是寻找到对称轴,若
图形两部分折叠后可重合,即可确定这个图形是轴对称图形,否则就不是轴对称图形.
轴对称
感悟新知
知识点
2
1. 定义
平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能够重合,那么称这两个图形成轴对称,这条直线就是对称轴. 折叠后重合的两点叫做对应点(也叫对称点).
感悟新知
特别解读
轴对称的三个条件:
1. 有两个图形;
2. 存在一条直线;
3. 一个图形沿着这条直线折叠后与另一个图形重合.
轴对称的两个特性:
1. 成轴对称的两个图形全等. 但全等的两个图形不一定成轴对称.
2. 轴对称是图形的一种全等变换.
感悟新知
2. 轴对称与轴对称图形的区别与联系
名称 轴对称 轴对称图形
区别 对象不同 两个图形 一个图形
意义不同 两个图形的特殊位置关系 一个具有特殊形状的图形
对称点位置不同 对称点分别在两个图形上 轴对称图形的对称轴一定经过这个图形的内部
对称轴位置不同 两个图形成轴对称,其对称轴可能在两个图形的外部,也可能经过两个图形的内部或它们的公共边(点) 轴对称图形的对称轴一定经过这个图形的内部
感悟新知
名称 轴对称 轴对称图形
区别 对称轴数量不同 只有一条对称轴 有一条或多条
联系 (1)定义中都有一条直线,都要沿着这条直线折叠
(2)把成轴对称的两个图形看成一个整体,它就是一个轴对称图形. 把一个轴对称图形沿对称轴分成两个图形,这两个图形关于这条轴对称
感悟新知
例2
[期末·北京朝阳区]如图15.1-1 下面镜子里哪个是他的像?( )
A. ① B. ② C. ③ D. ④
感悟新知
解题秘方:镜面对称的实质就是把平面镜看成对称轴,
若平面镜两旁的图形能对称,则根据定义就可得出答案.
感悟新知
方法点拨
镜面对称的本质就是以平面镜为对称轴的轴对称,而识别轴对称的方法:
1. 定义法:紧扣定义中的“两个图形,一条直线,完全重合”.
2. 反面观察法:从纸的反面观察图形,若观察到的和正面一样,就是轴对称.
感悟新知
解:由轴对称的性质,连接对应点的线段与镜面垂直并
且被镜面平分,即可得出只有②与原图形成镜面对称.
答案:B
感悟新知
1. 定义 经过线段的中点并且垂直于这条线段的直线叫做这条线段的垂直平分线,又叫做线段的中垂线.
线段的垂直平分线
知识点
3
特别解读
1. 线段的垂直平分线必须满足两个条件:
(1) 经过线段的中点;
(2) 垂直于这条线段. 两者缺一不可.
2. 线段的垂直平分线的定义反过来也成立.
感悟新知
2. 几何语言 如图15.1-2,
∵ DC ⊥ AB,AC=BC,
∴ DC 是AB 的垂直平分线.
反过来也成立:
∵ DC 是AB 的垂直平分线,
∴ DC ⊥ AB,AC=BC.
感悟新知
例 3
如图15.1-3,直线AE 是线段BC 的垂直平分线,垂足为E,D 是直线AE 上任意一点,
求证:∠ ABD= ∠ ACD.
感悟新知
解法提醒
1.由直线AE 是线段BC 的垂直平分线得出BE=CE,AE ⊥ BC. 这两个结论有时根据证题需要可只写出其中一
个结论.
2.若要证AE 是线段BC 的垂直平分线,则必须同时具备BE=CE,AE⊥ BC 这两个条件.
解题秘方:紧扣线段的垂直平分线的定义进行解答.
证明:∵直线AE 是线段BC 的垂直平分线,
∴ BE=CE,AE ⊥ BC. ∴∠ AEB= ∠ AEC=90° .
在Rt △ ABE 和Rt △ ACE 中, AE=AE,
∠ AEB= ∠ AEC,
BE=CE,
∴ Rt △ ABE ≌ Rt △ ACE.(SAS)
∴∠ ABE= ∠ ACE. 同理可证∠ DBE= ∠ DCE,
∴∠ ABE - ∠ DBE= ∠ ACE- ∠ DCE,即∠ ABD= ∠ ACD.
感悟新知
感悟新知
1. 轴对称的性质 如果两个图形关于某直线对
称,那么对称轴是任何一对对应点所连线
段的垂直平分线,如图15.1-4.
特别地:成轴对称的两个图形的对应
线段所在直线平行或者重合或者相交于某
一点,且该点一定在对称轴上.
2. 反之 成轴对称的两个图形中,对应点的连线被对称轴垂直平分.
轴对称的性质
知识点
4
感悟新知
特别解读
轴对称图形或成轴对称的两个图形的对应线段、对
应角相等;
2. 轴对称图形被对称轴分成的两部分全等,并且这两部分关于对称轴成轴对称. 成轴对称的两个图形也全等,但全等的两个图形不一定成轴对称.
感悟新知
[模拟·深圳]如图15.1-5,在△ ABC 中,点D,E
分别在边AB,BC 上, 点A 与点E 关于直线CD 对称. 若AB=7,AC=9,BC=12,则△ DBE 的周长为( )
A.9 B.10
C.11 D.12
例4
感悟新知
解法提醒
轴对称的性质中关键有两点:
一是对应图形的全等性,根据全等的性质可得到对应的边、角相等;
二是对称轴的垂直平分性. 揭示对称轴与对应点所连线段之间的位置关系.
解题秘方:根据轴对称的性质得到:AD=DE,AC=CE, 结合已知条件和三角形周长公式解答.
解:∵点A 与点E 关于直线CD 对称,
∴ AD=DE,AC=CE = 9.
∵ AB=7,AC=9,BC=12,
∴△ DBE 的周长=BD+DE+BE
=BD+AD+BC-AC
=AB+BC-AC
=7+12-9=10.
答案:B
感悟新知
感悟新知
例 5
如图15.1-6, △ ABC 中,D,E,F 三点分别在
AB,BC,AC 上,且四边形BEFD 是以DE 为对称轴的轴对称图形,四边形CFDE 是以FE 为对称轴的轴对称图形.若∠ C=40°,则∠ DFE 的度数为( )
A.65° B.70°
C.75° D.80°
感悟新知
解题秘方:根据轴对称的性质可得∠ BED= ∠ DEF=
∠ CEF,据此可得∠ DEF=60°,∠ EDF= ∠C=40°,再根据三角形的内角和定理可得
∠ DFE 的度数.
感悟新知
解法提醒
利用轴对称的性质求线段的长度或角的度数的方法:
先根据成轴对称的特征确定两个图形的对应边、对应角,再运用轴对称的性质(对应边相等,对应角相等),把要求的边或角与已知的对应边或对应角建立联系,从而求出待求的线段的长度或角的度数.
感悟新知
解:∵四边形BEFD 是以DE 为对称轴的轴对称图形,四
边形CFDE 是以FE 为对称轴的轴对称图形,
∴∠ BED= ∠ DEF= ∠ CEF= ,
∠ EDF= ∠ C=40°,
∴∠ DFE=180° - ∠ DEF- ∠ EDF=80° .
答案:D
轴对称图形
轴对称和轴对称图形的区别:
(1)定义不同;
(2)轴对称图形指的是一个图形,而两个图形成轴
对称指的是两个图形;
(3)一个轴对称图形的对称轴可能有多条,而两个
图形成轴对称的对称轴一般只有一条.
请完成教材课后习题
作业提升
