第一章 直角三角形的边角关系 章末复习课件(共37张PPT)
文档属性
| 名称 | 第一章 直角三角形的边角关系 章末复习课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 08:10:15 | ||
图片预览










文档简介
(共37张PPT)
第一章 直角三角形的边角关系
章末小结
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
知识框架
1、锐角三角函数的概念
2、特殊角的三角函数值
3、解直角三角形
4、借助计算器求一般角度数的三角函数
5、三角函数的实际应用
6、利用三角函数测高
知识归纳
知识点一 锐角三角函数的概念
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
如图所示,在Rt△ABC中,∠C=90°,
a,b,c分别是∠A,∠B,∠C的对边.
(1) ∠A的正弦:
∠A的对边
斜边
sin A =
∠A的邻边
斜边
∠A的邻边
∠A的对边
知识点二 特殊角的三角函数值
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
1
(1) 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,
∠B,∠C的对边.
三边关系: ;
三角关系:__________________;
边角关系:sinA=cosB=_______,cosA=sinB
=____,
tanA=____________,tanB=___________.
a2+b2=c2
∠A=90°-∠B
知识点三 解直角三角形
(2) 直角三角形可解的条件和解法
条件:解直角三角形时知道其中的2个元素(至少
有一个是边),就可以求出其余的3个未知元素.
解法:①一边一锐角,先由两锐角互余关系求出
另一锐角;知斜边,再用正弦(或余弦)求另两边;
知直角边用正切求另一直角边,再用正弦或勾股
定理求斜边;②知两边:先用勾股定理求另一边,
再用边角关系求锐角;③斜三角形问题可通过添
加适当的辅助线转化为解直角三角形问题.
(3) 互余两角的三角函数间的关系
sinα = ,
cosα = _____________,
sin2α + cos2α = .
tanα · tan(90°-α) =___.
cos(90°-α)
sin(90°-α)
1
1
对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越____.
大
小
(4) 锐角三角函数的增减性
(1) 利用计算器求三角函数值
第二步:输入角度值,
屏幕显示结果.
(也有的计算器是先输入角度再按函数名称键)
第一步:按计算器 键,
sin
tan
cos
知识点四 借助计算器求三角函数值和锐角
(2) 利用计算器求锐角的度数
还可以利用 键,进一步得到角的度数.
第二步:输入函数值
屏幕显示答案 (按实际需要进行精确)
方法①:
°'″
2nd F
第一步:按计算器 键,
2nd F
sin
cos
tan
方法②:
第二步:输入锐角函数值
屏幕显示答案 (按实际需要选取精确值).
第一步:按计算器 键,
°'″
2nd F
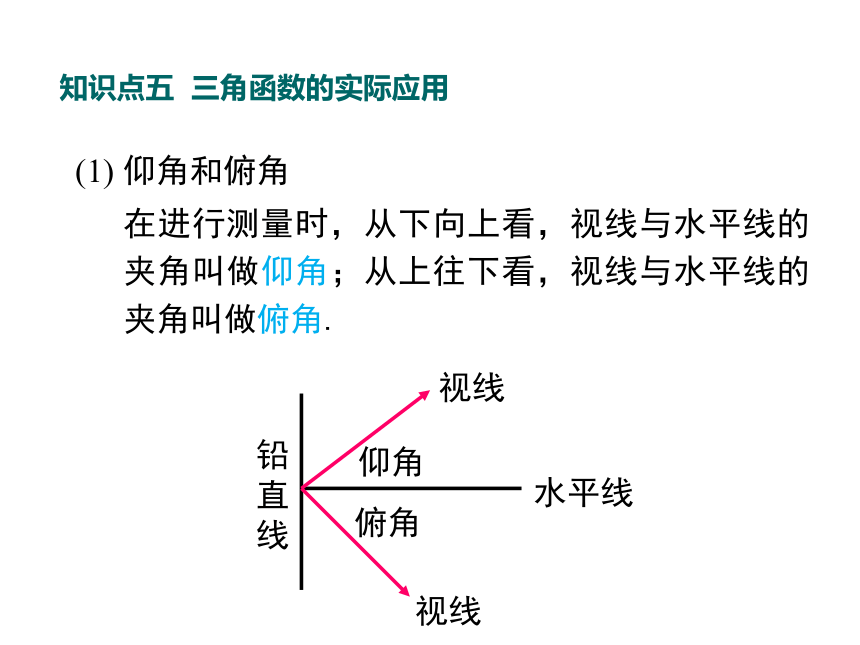
(1) 仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
知识点五 三角函数的实际应用
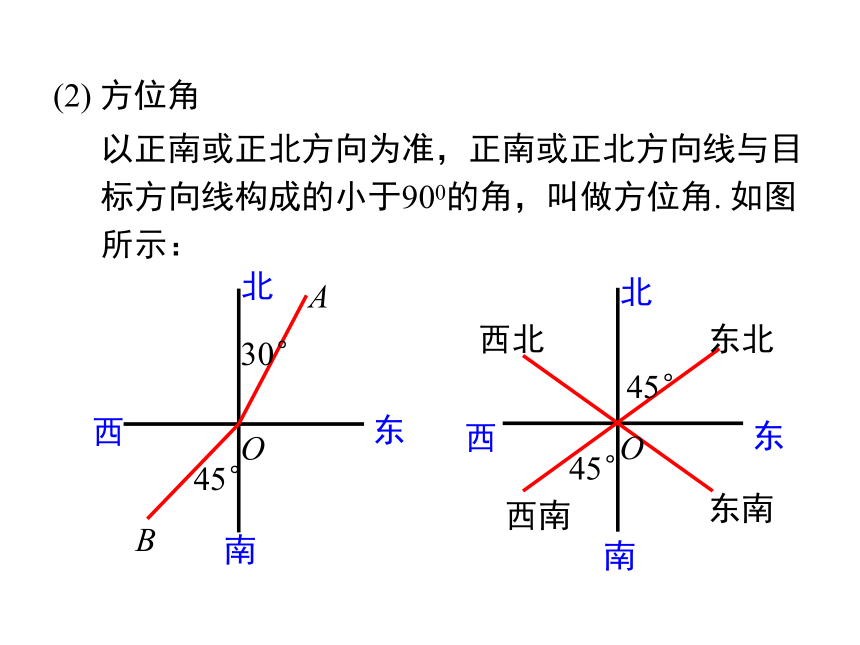
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于900的角,叫做方位角. 如图所示:
30°
45°
B
O
A
东
西
北
南
(2) 方位角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
坡面与水平面的夹角叫做坡角,记作α,有
i = tan α.
坡度通常写成1∶m的形式,如i=1∶6.
显然,坡度越大,坡角α就越大,
坡面就越陡.
如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度.记作i,即i = .
(3) 坡度,坡角
(4) 利用解直角三角形的知识解决实际问题的一般过
程是:
① 将实际问题抽象为数学问题(画出平面图形,
转化为解直角三角形的问题);
② 根据条件的特点,适当选用锐角三角函数等
去解直角三角形;
③ 得到数学问题的答案;
④ 得到实际问题的答案.
知识点六 利用三角函数测高
A
C
M
N
①在测点A安置测倾器,测得M的仰角∠MCE=α;
E
②量出测点A到物体底部N的水平距离AN=l;
③量出测倾器的高度AC=a,可求出
MN=ME+EN=l · tanα+a.
α
(1) 测量底部可以到达的物体的高度步骤:
(2) 测量东方明珠的高度的步骤是怎么样的呢?
①在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
A
C
B
D
M
N
E
α
②在测点A与物体之间的B处安置测倾器,测得此时M的仰角
∠MDE=β;
β
③量出测倾器的高度AC=BD=a,以及测点A,B之间的距离
AB=b.根据测量数据,可求出物体MN的高度.
典例精析
1.如图,P是 的边 OA 上一点,点 P的坐标为
,则 =__________.
M
记得构造直角三角形哦!
O
P(12,5)
A
x
y
2.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).
A
B
C
┌
解:
3.在等腰△ABC中, AB=AC=13, BC=10,求tanB.
提示:过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
解:如图,过点A作AD⊥BC于点D,
∴在Rt△ABD中,
易知BD=5,AD=12.
4.在Rt△ABC中,∠C=90°, AB=15,tanA= ,求AC和BC.
4k
┌
A
C
B
15
3k
5. 如图,在Rt△ABC中,∠C=90°,AB =10,BC=6,求sinA、cosA、tanA的值.
解:∵
又∵
A
B
C
6
10
6.求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
A
7.下列各式中一定成立的是( )
A.tan75°﹥tan48°﹥tan15°
B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15°
D. sin75°﹤sin48°8.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a = 30 , b = 20 ;
解:根据勾股定理得
A
B
C
b=20
a=30
c
(2) ∠B=72°,c = 14.
A
B
C
b
a
c=14
解:
9. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;
解:由题意,AC=AB=610(米).
A
E
B
C
D
39°
45°
A
E
B
C
D
39°
45°
(2) 求大楼的高度CD(精确到1米).
故BE=DEtan39°.
∵CD=AE,
∴CD=AB-DE·tan39°
=610-610×tan39°≈116(米).
解:DE=AC=610(米),
在Rt△BDE中,tan∠BDE= .
11. 如图有一个古镇建筑A,它周围800米内有古建筑,
乡村路要由西向东修筑,在B点处测得古建筑A在北
偏东60°方向上,向前直行1200米到达D点,这时
测得古建筑A在D点北偏东30°方向上,如果不改变
修筑的方向,你认为古建筑会不会遭到破坏?
D
B
A
E
答案:AE= 米.
>800,
所以古建筑会遭到破坏.
课堂练习
1:如图,在Rt△ABC中,∠C=90°,
cosA= ,求sinA、tanA的值.
解:∵
A
B
C
设AC=15k,则AB=17k
所以
∴
2:如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求sinA、cosB的值.
A
B
C
8
解:∵
3.如图,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=
(1)求点B的坐标;
(2)求cos∠BAO的值.
A
B
H
解:(1)如图所示,作BH⊥OA, 垂足为H.在Rt△OHB中,
∵BO=5,sin∠BOA= ,
∴BH=3,OH=4,
∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,
∴AH=6.
∵在Rt△AHB中,BH=3,
4. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形.
D
A
B
C
6
解:
∵AD平分∠BAC,
5. 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.
解:
A
C
B
设
∴AB的长为
解:作DE⊥AB,
CF⊥AB,
垂足分别为E、F.
由题意可知
DE=CF=4 (米),CD=EF=12 (米).
6. 一段路基的横断面是梯形,高为4米,上底的宽是
12米,路基的坡面与地面的倾角分别是45°和30°,
求路基下底的宽 (精确到0.1米, ,
).
45°
30°
4米
12米
A
B
C
D
在Rt△ADE中,
E
F
在Rt△BCF中,同理可得
因此 AB=AE+EF+BF≈4+12+6.93≈22.93 (米).
答: 路基下底的宽约为22.93米.
(米).
(米).
45°
30°
4米
12米
A
B
C
D
E
F
课堂小结
锐角三角函数
特殊角的三角函数
解直角三角形
简单实际问题
正弦
锐
角
三
角
函
数
余弦
正切
三边关系
三角关系
边角关系
仰俯角问题
方位角问题
坡度问题
第一章 直角三角形的边角关系
章末小结
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
知识框架
1、锐角三角函数的概念
2、特殊角的三角函数值
3、解直角三角形
4、借助计算器求一般角度数的三角函数
5、三角函数的实际应用
6、利用三角函数测高
知识归纳
知识点一 锐角三角函数的概念
(2)∠A的余弦:cosA= = ;
(3)∠A的正切:tanA= = .
如图所示,在Rt△ABC中,∠C=90°,
a,b,c分别是∠A,∠B,∠C的对边.
(1) ∠A的正弦:
∠A的对边
斜边
sin A =
∠A的邻边
斜边
∠A的邻边
∠A的对边
知识点二 特殊角的三角函数值
sin30°= ,sin45°= ,sin60°= ;
cos30°= ,cos45°= ,cos60°= ;
tan30°= ,tan45°= ,tan60°= .
1
(1) 在Rt△ABC中,∠C=90°,a,b,c分别是∠A,
∠B,∠C的对边.
三边关系: ;
三角关系:__________________;
边角关系:sinA=cosB=_______,cosA=sinB
=____,
tanA=____________,tanB=___________.
a2+b2=c2
∠A=90°-∠B
知识点三 解直角三角形
(2) 直角三角形可解的条件和解法
条件:解直角三角形时知道其中的2个元素(至少
有一个是边),就可以求出其余的3个未知元素.
解法:①一边一锐角,先由两锐角互余关系求出
另一锐角;知斜边,再用正弦(或余弦)求另两边;
知直角边用正切求另一直角边,再用正弦或勾股
定理求斜边;②知两边:先用勾股定理求另一边,
再用边角关系求锐角;③斜三角形问题可通过添
加适当的辅助线转化为解直角三角形问题.
(3) 互余两角的三角函数间的关系
sinα = ,
cosα = _____________,
sin2α + cos2α = .
tanα · tan(90°-α) =___.
cos(90°-α)
sin(90°-α)
1
1
对于sinα与tanα,角度越大,函数值越 ;
对于cosα,角度越大,函数值越____.
大
小
(4) 锐角三角函数的增减性
(1) 利用计算器求三角函数值
第二步:输入角度值,
屏幕显示结果.
(也有的计算器是先输入角度再按函数名称键)
第一步:按计算器 键,
sin
tan
cos
知识点四 借助计算器求三角函数值和锐角
(2) 利用计算器求锐角的度数
还可以利用 键,进一步得到角的度数.
第二步:输入函数值
屏幕显示答案 (按实际需要进行精确)
方法①:
°'″
2nd F
第一步:按计算器 键,
2nd F
sin
cos
tan
方法②:
第二步:输入锐角函数值
屏幕显示答案 (按实际需要选取精确值).
第一步:按计算器 键,
°'″
2nd F
(1) 仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
知识点五 三角函数的实际应用
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于900的角,叫做方位角. 如图所示:
30°
45°
B
O
A
东
西
北
南
(2) 方位角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
坡面与水平面的夹角叫做坡角,记作α,有
i = tan α.
坡度通常写成1∶m的形式,如i=1∶6.
显然,坡度越大,坡角α就越大,
坡面就越陡.
如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度.记作i,即i = .
(3) 坡度,坡角
(4) 利用解直角三角形的知识解决实际问题的一般过
程是:
① 将实际问题抽象为数学问题(画出平面图形,
转化为解直角三角形的问题);
② 根据条件的特点,适当选用锐角三角函数等
去解直角三角形;
③ 得到数学问题的答案;
④ 得到实际问题的答案.
知识点六 利用三角函数测高
A
C
M
N
①在测点A安置测倾器,测得M的仰角∠MCE=α;
E
②量出测点A到物体底部N的水平距离AN=l;
③量出测倾器的高度AC=a,可求出
MN=ME+EN=l · tanα+a.
α
(1) 测量底部可以到达的物体的高度步骤:
(2) 测量东方明珠的高度的步骤是怎么样的呢?
①在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
A
C
B
D
M
N
E
α
②在测点A与物体之间的B处安置测倾器,测得此时M的仰角
∠MDE=β;
β
③量出测倾器的高度AC=BD=a,以及测点A,B之间的距离
AB=b.根据测量数据,可求出物体MN的高度.
典例精析
1.如图,P是 的边 OA 上一点,点 P的坐标为
,则 =__________.
M
记得构造直角三角形哦!
O
P(12,5)
A
x
y
2.如图,某人从山脚下的点A走了200m后到达山顶的点B.已知山顶B到山脚下的垂直距离是55m,求山坡的坡度(结果精确到0.001m).
A
B
C
┌
解:
3.在等腰△ABC中, AB=AC=13, BC=10,求tanB.
提示:过点A作AD垂直于BC于点D.
求锐角三角函数时,勾股定理的运用是很重要的.
A
C
B
┌
D
解:如图,过点A作AD⊥BC于点D,
∴在Rt△ABD中,
易知BD=5,AD=12.
4.在Rt△ABC中,∠C=90°, AB=15,tanA= ,求AC和BC.
4k
┌
A
C
B
15
3k
5. 如图,在Rt△ABC中,∠C=90°,AB =10,BC=6,求sinA、cosA、tanA的值.
解:∵
又∵
A
B
C
6
10
6.求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
A
7.下列各式中一定成立的是( )
A.tan75°﹥tan48°﹥tan15°
B. tan75°﹤tan48°﹤tan15°
C. cos75°﹥cos48°﹥cos15°
D. sin75°﹤sin48°
(1)a = 30 , b = 20 ;
解:根据勾股定理得
A
B
C
b=20
a=30
c
(2) ∠B=72°,c = 14.
A
B
C
b
a
c=14
解:
9. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)
(1) 求大楼与电视塔之间的距离AC;
解:由题意,AC=AB=610(米).
A
E
B
C
D
39°
45°
A
E
B
C
D
39°
45°
(2) 求大楼的高度CD(精确到1米).
故BE=DEtan39°.
∵CD=AE,
∴CD=AB-DE·tan39°
=610-610×tan39°≈116(米).
解:DE=AC=610(米),
在Rt△BDE中,tan∠BDE= .
11. 如图有一个古镇建筑A,它周围800米内有古建筑,
乡村路要由西向东修筑,在B点处测得古建筑A在北
偏东60°方向上,向前直行1200米到达D点,这时
测得古建筑A在D点北偏东30°方向上,如果不改变
修筑的方向,你认为古建筑会不会遭到破坏?
D
B
A
E
答案:AE= 米.
>800,
所以古建筑会遭到破坏.
课堂练习
1:如图,在Rt△ABC中,∠C=90°,
cosA= ,求sinA、tanA的值.
解:∵
A
B
C
设AC=15k,则AB=17k
所以
∴
2:如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求sinA、cosB的值.
A
B
C
8
解:∵
3.如图,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=
(1)求点B的坐标;
(2)求cos∠BAO的值.
A
B
H
解:(1)如图所示,作BH⊥OA, 垂足为H.在Rt△OHB中,
∵BO=5,sin∠BOA= ,
∴BH=3,OH=4,
∴点B的坐标为(4,3).
(2)∵OA=10,OH=4,
∴AH=6.
∵在Rt△AHB中,BH=3,
4. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,解这个直角三角形.
D
A
B
C
6
解:
∵AD平分∠BAC,
5. 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.
解:
A
C
B
设
∴AB的长为
解:作DE⊥AB,
CF⊥AB,
垂足分别为E、F.
由题意可知
DE=CF=4 (米),CD=EF=12 (米).
6. 一段路基的横断面是梯形,高为4米,上底的宽是
12米,路基的坡面与地面的倾角分别是45°和30°,
求路基下底的宽 (精确到0.1米, ,
).
45°
30°
4米
12米
A
B
C
D
在Rt△ADE中,
E
F
在Rt△BCF中,同理可得
因此 AB=AE+EF+BF≈4+12+6.93≈22.93 (米).
答: 路基下底的宽约为22.93米.
(米).
(米).
45°
30°
4米
12米
A
B
C
D
E
F
课堂小结
锐角三角函数
特殊角的三角函数
解直角三角形
简单实际问题
正弦
锐
角
三
角
函
数
余弦
正切
三边关系
三角关系
边角关系
仰俯角问题
方位角问题
坡度问题
