1.6 利用三角函数测高 课件(共43张PPT)
文档属性
| 名称 | 1.6 利用三角函数测高 课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 08:12:18 | ||
图片预览






文档简介
(共43张PPT)
第一章 直角三角形的边角关系
1.6 利用三角函数测高
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握坡度、坡比的概念,并灵活运用坡度、坡比的概念求出物体的高度;
2、能够设计活动方案、自制测倾器和运用测倾器进行实地测量以及撰写活动报告的过程;
3、能够综合运用直角三角形边角关系的知识解决实际问题.
导入新课
观察与思考
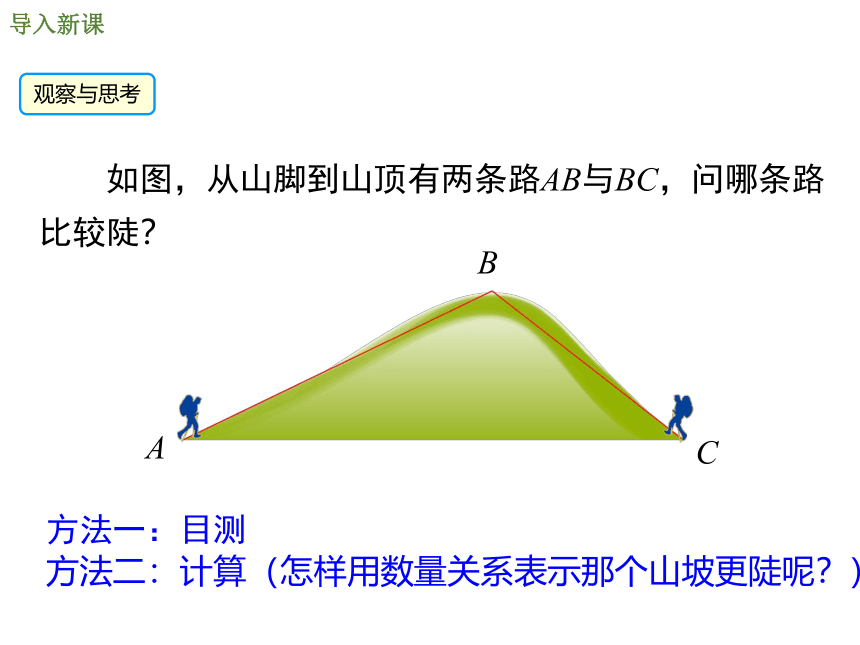
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
方法一:目测
方法二:计算(怎样用数量关系表示那个山坡更陡呢?)
A
B
C
讲授新课
知识点一 与坡度、坡角有关的实际问题
α
l
h
i= h : l
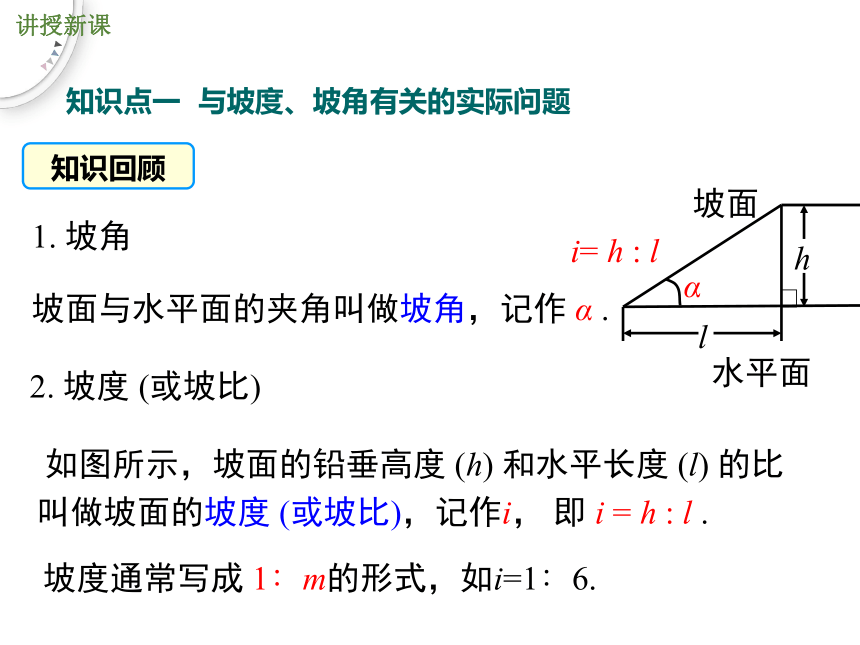
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
坡度通常写成 1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l .
坡面
水平面
知识回顾
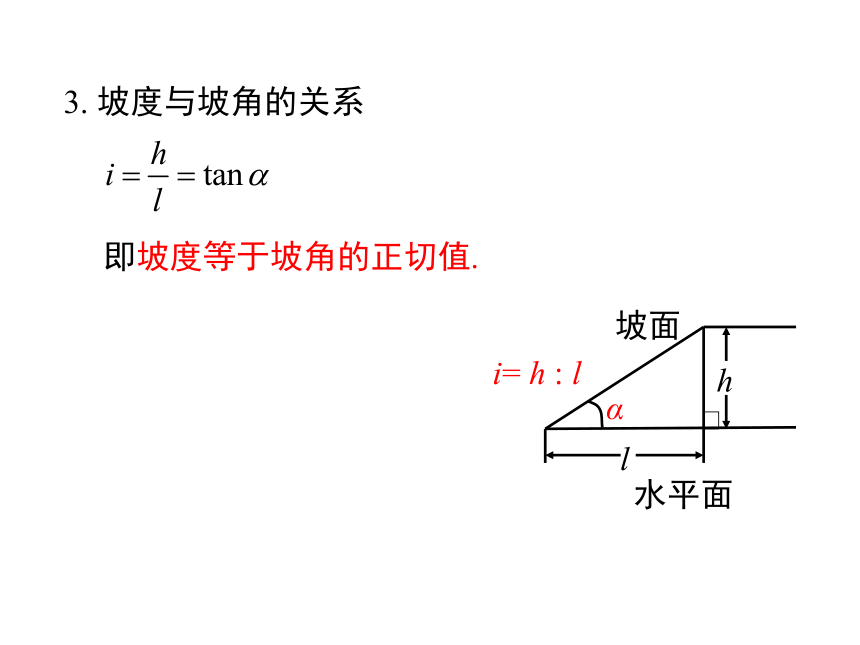
3. 坡度与坡角的关系
即坡度等于坡角的正切值.
α
l
h
i= h : l
坡面
水平面
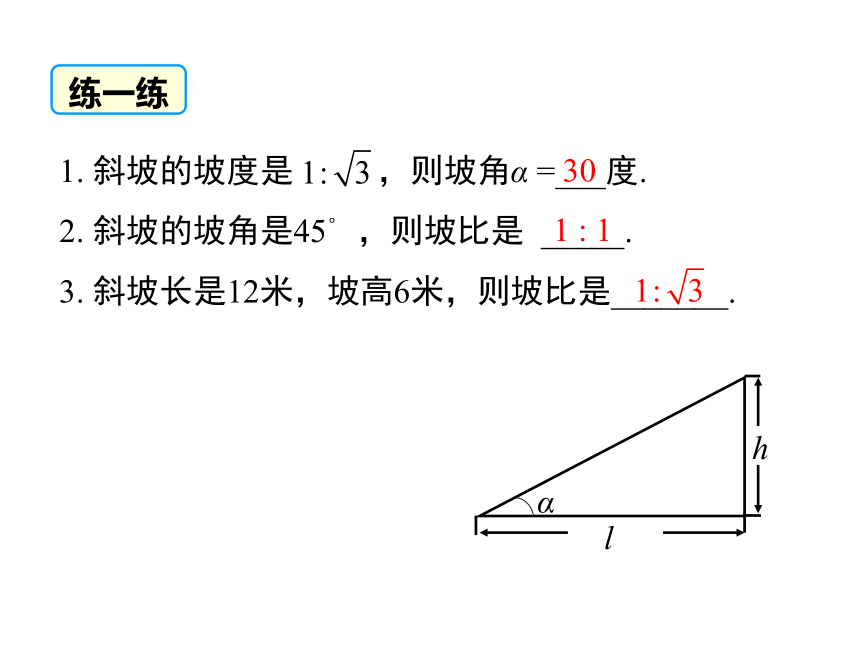
1. 斜坡的坡度是 ,则坡角α =___度.
2. 斜坡的坡角是45° ,则坡比是 _____.
3. 斜坡长是12米,坡高6米,则坡比是_______.
α
l
h
30
1 : 1
练一练
例1 如图,一山坡的坡度为i=1:2.小刚从山脚A出发,
沿山坡向上走了240m到达点C.这座山坡的坡角是多
少度?小刚上升了多少米(角度精确到0.01°,长
度精确到0.1m)?
i=1:2
典例精析
在Rt△ABC中,∠B=90°,∠A=26.57°,
AC=240m,
解:
用α表示坡角的大小,由题意可得
因此 α≈26.57°.
答:这座山坡的坡角约为26.57°,小刚上
升了约107.3 m.
从而 BC=240×sin26.57°≈107.3(m).
因此
例2 铁路路基的横断面是四边形ABCD,AD∥BC,路基宽BC=9.8m,高BE=5.8m,斜坡AB的坡度i=1∶1.6,斜坡CD的坡度i=1∶2.5,求:底宽AB和斜坡的坡角α和β (精确到 1°);
A
D
B
C
i=1:2.5
5.8
9.8
α
i=1:1.6
解: 过C作CF⊥AD于点F,得
CF=BE,EF=BC,∠A=α,∠B=β.
β
F
∴AE=1.6×5.8=9.28(m),DF=2.5×5.8=14.5(m).
∴AD=AE+EF+DF=9.28+9.8+14.5≈33.6(m).
答:铁路路基下底宽为33.6m,斜坡的坡角分别为32°和21°
E
F
A
D
B
C
i=1:2.5
5.8
9.8
α
i=1:1.6
β
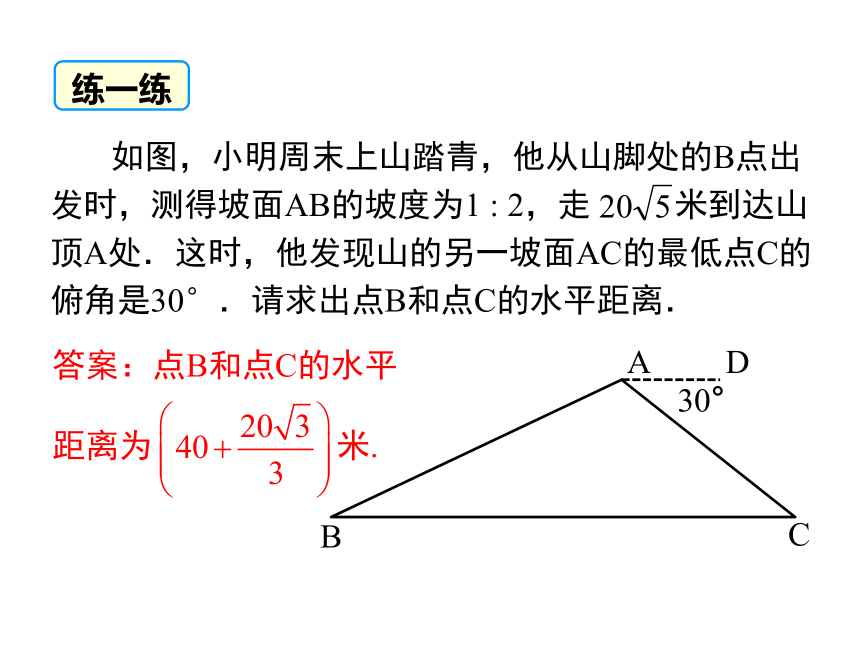
如图,小明周末上山踏青,他从山脚处的B点出发时,测得坡面AB的坡度为1 : 2,走 米到达山顶A处.这时,他发现山的另一坡面AC的最低点C的俯角是30°.请求出点B和点C的水平距离.
练一练
A
C
B
D
30°
答案:点B和点C的水平距离为 米.
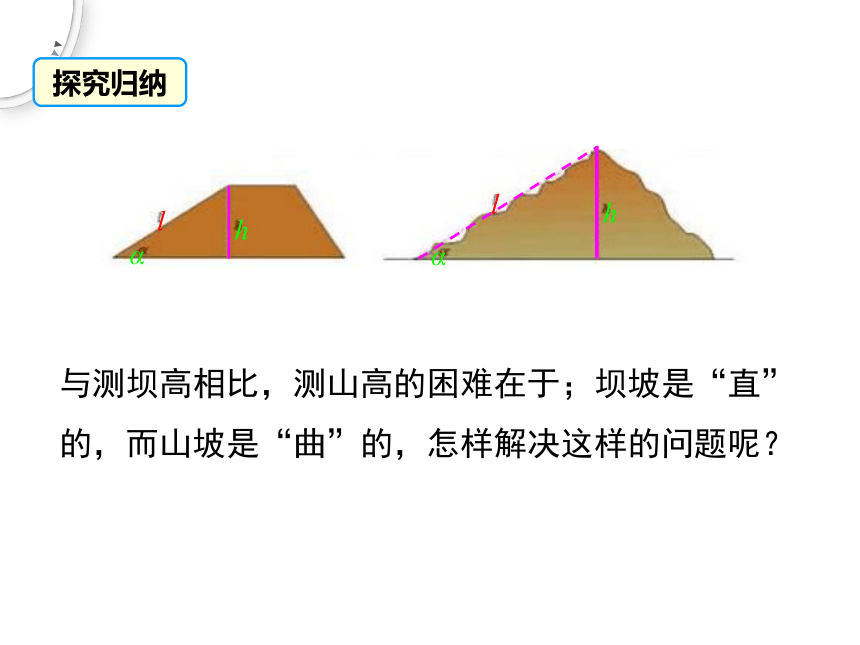
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
h
h
α
α
l
l
探究归纳
我们设法“化曲为直,以直代曲”. 我们可以把山坡“化整为零”地划分为一些小段,如图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角α1,这样就可以算出这段山坡的高度h1=l1sinα1.
h1
α1
l1
知识点二 测量倾斜角
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
问题1:如何测量倾斜角?
测量倾斜角可以用测倾器,
----简单的侧倾器由度盘、铅锤和支杆组成
0
30
30
60
60
90
90
1.把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
P
Q
问题2:如何使用测倾器?
0
30
30
60
60
90
90
2.转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
M
30°
知识点三 测量底部可以到达的物体的高度
问题1:如何测量旗杆的高度?
A
C
M
N
E
在现实生活中,我们可以直接在旗杆下来回行走,所以只需测量一次角度(如图中的α)就可以确定旗杆的高度.
α
所谓“底部可以到达”,就是
在地面上可以无障碍地直接
测得测点与被测物体的
底部之间的距离,
如图CE的长度.
A
C
M
N
1.在测点A安置测倾器,测得M的仰角∠MCE=α;
E
2.量出测点A到物体底部N的水平距离AN=l;
3.量出测倾器的高度AC=a,可求出MN的高度.
MN=ME+EN=l·tanα+a
α
问题2:测量旗杆的高度的步骤是怎么样的呢?
例3 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
典例精析
解:如图,作EM垂直CD于M点,根据题意,可知
EB=1.4m∠DEM=30°,BC=EM=30 m, CM=BE=1.4m
M
在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4=18.72(m).
知识点四 测量底部不可以到达的物体的高度
问题1:在黄浦江的另一端,你能否测量东方明珠的高度呢?
所谓“底部不可以到达”,就是
在地面上不能直接测得测点与被测物体的底部之间的距离,
如图中的AN或BN的长度.
A
C
B
D
M
N
E
α
β
在现实生活中,我们不可以直接从被测点到达被测点的脚下,这时我们能利用两次测量仰角(图中α和β),再结合解三角形的知识来求出东方明珠的高度.
问题2:测量东方明珠的高度的步骤是怎么样的呢?
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
A
C
B
D
M
N
E
α
2.在测点A与物体之间的B处安置测倾器,测得此时M的仰角∠MDE=β;
β
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.
当堂练习
1.如图,窗子高AB=m米,窗子外面上方0.2米的点C处安装水平遮阳板CD=1米,当太阳光线与水平线成α=60°角时,光线刚好不能直接射人室内,则m的值是( )
A.m=+0.8 B.m=+0.2
C.m=-0.2 D.m=-0.8
【答案】C
【详解】∵CD=1米,∠CDB=a=60°,
∴BC=CD·tanα=1×=,
∴m=AB=BC-AC=-0.2,
故选:C.
2.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( )
A. B. C. D.
【答案】A
【详解】设CD=x,在Rt△ADC中,∠A=45°,
∴CD=AD=x,
∴BD=16-x,
在Rt△BCD中,∠B=60°,
∴tanB=,
即:,
解得x=8(3-),
故选A.
3.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点之间的距离为35米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.35sinα米 B.米 C.35cosα米 D.米
【答案】A
【分析】在Rt△ABC中,已知∠BAC和斜边AB,求∠BAC的对边,选择∠BAC的正弦,列出等式即可表示出来.
【详解】在Rt△ABC中,
sin∠BAC=,
即sinα=,BC=35·sinα
故选:A.
4.一配电房示意图如图所示,它是一个轴对称图形,已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m
C.(4+)m D.(4+)m
【答案】B
【分析】过点A作AD⊥BC于D,根据轴对称图形得性质即可得BD=CD,从而利用锐角三角函数正切值即可求得答案.
5.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠α=45°,∠β=30°,则竹竿AB与AD的长度之比为__________.
【答案】
【点睛】本题主要考查解直角三角形的应用,解题的关键是掌握正弦函数的定义及其应用.
6.如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为_____m.(结果保留根号)
【答案】(30+30).
【分析】在Rt△ABD中,根据正切函数求得BD=AD tan∠BAD,在Rt△ACD中,求得CD=AD tan∠CAD,再根据BC=BD+CD,代入数据计算即可.
【详解】解:∵在Rt△ABD中,AD=90,∠BAD=45°,
∴BD=AD=30(m),
∵在Rt△ACD中,∠CAD=60°,
∴CD=AD tan60°=30×=30(m),
∴BC=BD+CD=30+30(m)
答:该建筑物的高度BC约为(30+30)米.
故答案为:(30+30).
7.如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18m的地面上,若测角仪的高度为I.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是____.
【详解】解:作DE⊥AB于E,
在Rt△ADE中,tan∠ADE=,
∴AE=DE tan∠ADE=18×=18,
∴AB=AE+EB=18+1.5=19.5(m),
故答案为:19.5m.
8.如图,小丽的房间内有一张长200m,高50cm的床靠墙摆放,在上方安装空调,空调下沿与EF墙垂直,出风口F离墙20cm,空调开启后,挡风板FG与EF夹角成136°,风沿FG方向吹出,为了让空调风不直接吹到床上,空调安装的高度(BC的长)至少为_________cm_(精确到个位)(参考数据:cos46°≈0.69,tan46°≈1.04,sin46°≈0.72)
【答案】
【分析】连接AF,作FH⊥AD构造直角三角形运用三角函数解出FH,再将床高加上即可求出EC的值.
【详解】当A、F在一条直线时,就正好不会吹到床上,连接AF,过点F作FH⊥AD,
∵AD=200,HD=20,
∴AH=180,
∵∠EFA=136°,
∴∠FAD=46°,
∴FH=AH·tan46°=180×1.04=187.2
∴ED=FH=187.2,
∴EC=187.2+50=237.2≈237.
故答案为237.
9.如图,甲 乙两楼相距30m,甲楼高40m,自甲楼楼顶看乙楼楼顶,仰角为30°,乙楼有多高?(结果精确到1m)
【答案】57m
【分析】先根据题意作出示意图,然后在RT△ACE中,可得出CE的长度,继而可得出乙楼的高度.
【详解】解:由题意得:
∠CAE=30°,AE=BD=30m,
在Rt△ACE中,CE=AE tan∠CAE=10m,
故可得乙楼的高度=CE+ED=CE+AB=(40+10)m≈57m.
10.数学课外学习小组利用矩形建筑物ABED测量广场灯塔CF的高,如图所示,在点B处测得灯塔顶端C的仰角为28°,在点D处测得灯塔顶端C的仰角为45°,已知AB=10m,AD=30m.求灯塔CF的高(结果保留整数).
(参考数据:tan28°≈0.53, cos28°≈0.88,sin28°≈0.47,≈1.41)
【详解】解:延长BE交CD于点G,交CF于点H,
在Rt△DEG中,∠EDG=45°,
∴EG=DE=10m.∠EGD=45°
设CH=xm,
在Rt△CGH中,∠CGH=∠EGD=45°,
∴GH=xm
在Rt△CBH中,∠CBH=28°,
∴tan∠CBH=,
即:=tan28°
解这个方程得:x≈45.1,
经检验:x≈45.1符合题意.
∴灯塔的高CF=55.1≈55(m)
答:灯塔的高为55米.
课堂小结
α
l
h
i= h : l
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l .
坡面
水平面
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
第一章 直角三角形的边角关系
1.6 利用三角函数测高
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握坡度、坡比的概念,并灵活运用坡度、坡比的概念求出物体的高度;
2、能够设计活动方案、自制测倾器和运用测倾器进行实地测量以及撰写活动报告的过程;
3、能够综合运用直角三角形边角关系的知识解决实际问题.
导入新课
观察与思考
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
方法一:目测
方法二:计算(怎样用数量关系表示那个山坡更陡呢?)
A
B
C
讲授新课
知识点一 与坡度、坡角有关的实际问题
α
l
h
i= h : l
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
坡度通常写成 1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l .
坡面
水平面
知识回顾
3. 坡度与坡角的关系
即坡度等于坡角的正切值.
α
l
h
i= h : l
坡面
水平面
1. 斜坡的坡度是 ,则坡角α =___度.
2. 斜坡的坡角是45° ,则坡比是 _____.
3. 斜坡长是12米,坡高6米,则坡比是_______.
α
l
h
30
1 : 1
练一练
例1 如图,一山坡的坡度为i=1:2.小刚从山脚A出发,
沿山坡向上走了240m到达点C.这座山坡的坡角是多
少度?小刚上升了多少米(角度精确到0.01°,长
度精确到0.1m)?
i=1:2
典例精析
在Rt△ABC中,∠B=90°,∠A=26.57°,
AC=240m,
解:
用α表示坡角的大小,由题意可得
因此 α≈26.57°.
答:这座山坡的坡角约为26.57°,小刚上
升了约107.3 m.
从而 BC=240×sin26.57°≈107.3(m).
因此
例2 铁路路基的横断面是四边形ABCD,AD∥BC,路基宽BC=9.8m,高BE=5.8m,斜坡AB的坡度i=1∶1.6,斜坡CD的坡度i=1∶2.5,求:底宽AB和斜坡的坡角α和β (精确到 1°);
A
D
B
C
i=1:2.5
5.8
9.8
α
i=1:1.6
解: 过C作CF⊥AD于点F,得
CF=BE,EF=BC,∠A=α,∠B=β.
β
F
∴AE=1.6×5.8=9.28(m),DF=2.5×5.8=14.5(m).
∴AD=AE+EF+DF=9.28+9.8+14.5≈33.6(m).
答:铁路路基下底宽为33.6m,斜坡的坡角分别为32°和21°
E
F
A
D
B
C
i=1:2.5
5.8
9.8
α
i=1:1.6
β
如图,小明周末上山踏青,他从山脚处的B点出发时,测得坡面AB的坡度为1 : 2,走 米到达山顶A处.这时,他发现山的另一坡面AC的最低点C的俯角是30°.请求出点B和点C的水平距离.
练一练
A
C
B
D
30°
答案:点B和点C的水平距离为 米.
与测坝高相比,测山高的困难在于;坝坡是“直”的,而山坡是“曲”的,怎样解决这样的问题呢?
h
h
α
α
l
l
探究归纳
我们设法“化曲为直,以直代曲”. 我们可以把山坡“化整为零”地划分为一些小段,如图表示其中一部分小段,划分小段时,注意使每一小段上的山坡近似是“直”的,可以量出这段坡长l1,测出相应的仰角α1,这样就可以算出这段山坡的高度h1=l1sinα1.
h1
α1
l1
知识点二 测量倾斜角
0
30
30
60
60
90
90
P
Q
度盘
铅锤
支杆
问题1:如何测量倾斜角?
测量倾斜角可以用测倾器,
----简单的侧倾器由度盘、铅锤和支杆组成
0
30
30
60
60
90
90
1.把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
P
Q
问题2:如何使用测倾器?
0
30
30
60
60
90
90
2.转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数.
M
30°
知识点三 测量底部可以到达的物体的高度
问题1:如何测量旗杆的高度?
A
C
M
N
E
在现实生活中,我们可以直接在旗杆下来回行走,所以只需测量一次角度(如图中的α)就可以确定旗杆的高度.
α
所谓“底部可以到达”,就是
在地面上可以无障碍地直接
测得测点与被测物体的
底部之间的距离,
如图CE的长度.
A
C
M
N
1.在测点A安置测倾器,测得M的仰角∠MCE=α;
E
2.量出测点A到物体底部N的水平距离AN=l;
3.量出测倾器的高度AC=a,可求出MN的高度.
MN=ME+EN=l·tanα+a
α
问题2:测量旗杆的高度的步骤是怎么样的呢?
例3 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗.经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时侧倾器离地面1.4m,求学校主楼的高度(精确到0.01m).
典例精析
解:如图,作EM垂直CD于M点,根据题意,可知
EB=1.4m∠DEM=30°,BC=EM=30 m, CM=BE=1.4m
M
在Rt△DEM中,DM=EMtan30°≈30×0.577 =17.32(m),
CD=DM+CM=17.32+1.4=18.72(m).
知识点四 测量底部不可以到达的物体的高度
问题1:在黄浦江的另一端,你能否测量东方明珠的高度呢?
所谓“底部不可以到达”,就是
在地面上不能直接测得测点与被测物体的底部之间的距离,
如图中的AN或BN的长度.
A
C
B
D
M
N
E
α
β
在现实生活中,我们不可以直接从被测点到达被测点的脚下,这时我们能利用两次测量仰角(图中α和β),再结合解三角形的知识来求出东方明珠的高度.
问题2:测量东方明珠的高度的步骤是怎么样的呢?
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
A
C
B
D
M
N
E
α
2.在测点A与物体之间的B处安置测倾器,测得此时M的仰角∠MDE=β;
β
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.根据测量数据,可求出物体MN的高度.
当堂练习
1.如图,窗子高AB=m米,窗子外面上方0.2米的点C处安装水平遮阳板CD=1米,当太阳光线与水平线成α=60°角时,光线刚好不能直接射人室内,则m的值是( )
A.m=+0.8 B.m=+0.2
C.m=-0.2 D.m=-0.8
【答案】C
【详解】∵CD=1米,∠CDB=a=60°,
∴BC=CD·tanα=1×=,
∴m=AB=BC-AC=-0.2,
故选:C.
2.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( )
A. B. C. D.
【答案】A
【详解】设CD=x,在Rt△ADC中,∠A=45°,
∴CD=AD=x,
∴BD=16-x,
在Rt△BCD中,∠B=60°,
∴tanB=,
即:,
解得x=8(3-),
故选A.
3.如图是净月潭国家森林公园一段索道的示意图.已知A、B两点之间的距离为35米,∠A=α,则缆车从A点到达B点,上升的高度(BC的长)为( )
A.35sinα米 B.米 C.35cosα米 D.米
【答案】A
【分析】在Rt△ABC中,已知∠BAC和斜边AB,求∠BAC的对边,选择∠BAC的正弦,列出等式即可表示出来.
【详解】在Rt△ABC中,
sin∠BAC=,
即sinα=,BC=35·sinα
故选:A.
4.一配电房示意图如图所示,它是一个轴对称图形,已知BC=6m,∠ABC=α,则房顶A离地面EF的高度为( )
A.(4+3sinα)m B.(4+3tanα)m
C.(4+)m D.(4+)m
【答案】B
【分析】过点A作AD⊥BC于D,根据轴对称图形得性质即可得BD=CD,从而利用锐角三角函数正切值即可求得答案.
5.如图,两根竹竿AB和AD斜靠在墙CE上,量得∠α=45°,∠β=30°,则竹竿AB与AD的长度之比为__________.
【答案】
【点睛】本题主要考查解直角三角形的应用,解题的关键是掌握正弦函数的定义及其应用.
6.如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为_____m.(结果保留根号)
【答案】(30+30).
【分析】在Rt△ABD中,根据正切函数求得BD=AD tan∠BAD,在Rt△ACD中,求得CD=AD tan∠CAD,再根据BC=BD+CD,代入数据计算即可.
【详解】解:∵在Rt△ABD中,AD=90,∠BAD=45°,
∴BD=AD=30(m),
∵在Rt△ACD中,∠CAD=60°,
∴CD=AD tan60°=30×=30(m),
∴BC=BD+CD=30+30(m)
答:该建筑物的高度BC约为(30+30)米.
故答案为:(30+30).
7.如图,小亮为了测量校园里教学楼AB的高度,将测角仪CD竖直放置在与教学楼水平距离为18m的地面上,若测角仪的高度为I.5m,测得教学楼的顶部A处的仰角为30°,则教学楼的高度是____.
【详解】解:作DE⊥AB于E,
在Rt△ADE中,tan∠ADE=,
∴AE=DE tan∠ADE=18×=18,
∴AB=AE+EB=18+1.5=19.5(m),
故答案为:19.5m.
8.如图,小丽的房间内有一张长200m,高50cm的床靠墙摆放,在上方安装空调,空调下沿与EF墙垂直,出风口F离墙20cm,空调开启后,挡风板FG与EF夹角成136°,风沿FG方向吹出,为了让空调风不直接吹到床上,空调安装的高度(BC的长)至少为_________cm_(精确到个位)(参考数据:cos46°≈0.69,tan46°≈1.04,sin46°≈0.72)
【答案】
【分析】连接AF,作FH⊥AD构造直角三角形运用三角函数解出FH,再将床高加上即可求出EC的值.
【详解】当A、F在一条直线时,就正好不会吹到床上,连接AF,过点F作FH⊥AD,
∵AD=200,HD=20,
∴AH=180,
∵∠EFA=136°,
∴∠FAD=46°,
∴FH=AH·tan46°=180×1.04=187.2
∴ED=FH=187.2,
∴EC=187.2+50=237.2≈237.
故答案为237.
9.如图,甲 乙两楼相距30m,甲楼高40m,自甲楼楼顶看乙楼楼顶,仰角为30°,乙楼有多高?(结果精确到1m)
【答案】57m
【分析】先根据题意作出示意图,然后在RT△ACE中,可得出CE的长度,继而可得出乙楼的高度.
【详解】解:由题意得:
∠CAE=30°,AE=BD=30m,
在Rt△ACE中,CE=AE tan∠CAE=10m,
故可得乙楼的高度=CE+ED=CE+AB=(40+10)m≈57m.
10.数学课外学习小组利用矩形建筑物ABED测量广场灯塔CF的高,如图所示,在点B处测得灯塔顶端C的仰角为28°,在点D处测得灯塔顶端C的仰角为45°,已知AB=10m,AD=30m.求灯塔CF的高(结果保留整数).
(参考数据:tan28°≈0.53, cos28°≈0.88,sin28°≈0.47,≈1.41)
【详解】解:延长BE交CD于点G,交CF于点H,
在Rt△DEG中,∠EDG=45°,
∴EG=DE=10m.∠EGD=45°
设CH=xm,
在Rt△CGH中,∠CGH=∠EGD=45°,
∴GH=xm
在Rt△CBH中,∠CBH=28°,
∴tan∠CBH=,
即:=tan28°
解这个方程得:x≈45.1,
经检验:x≈45.1符合题意.
∴灯塔的高CF=55.1≈55(m)
答:灯塔的高为55米.
课堂小结
α
l
h
i= h : l
1. 坡角
坡面与水平面的夹角叫做坡角,记作 α .
2. 坡度 (或坡比)
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l .
坡面
水平面
利用三角函数测高
测倾器的认识及使用
测量底部可以到达的物体的高度(一次测量仰角)
测量底部不可以到达的物体的高度(两次测量仰角)
利用解三角形的知识,求出物体的高度
