27.2 圆心角、弧、弦、弦心距之间的关系(第3课时) 课件(共24张PPT)
文档属性
| 名称 | 27.2 圆心角、弧、弦、弦心距之间的关系(第3课时) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 08:14:45 | ||
图片预览






文档简介
(共24张PPT)
2022-2023学年九年级数学下册同步精品课堂(沪教版)
第 27 章 圆与正多边形
27.2圆心角、弧 弦、弦心距之间的关系(第3课时)
1.理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问
题.(重点)
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”
条件的意义.(难点)
学习目标
在同圆或等圆中,如果两个圆心角、两条劣弧(或优弧)、两条弦、两条弦的弦心距的四组量中有一组量相等,那么它们所对应的其余三组量也分别相等.
复习引入
在同圆或等圆中
题设
结论
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
复习引入
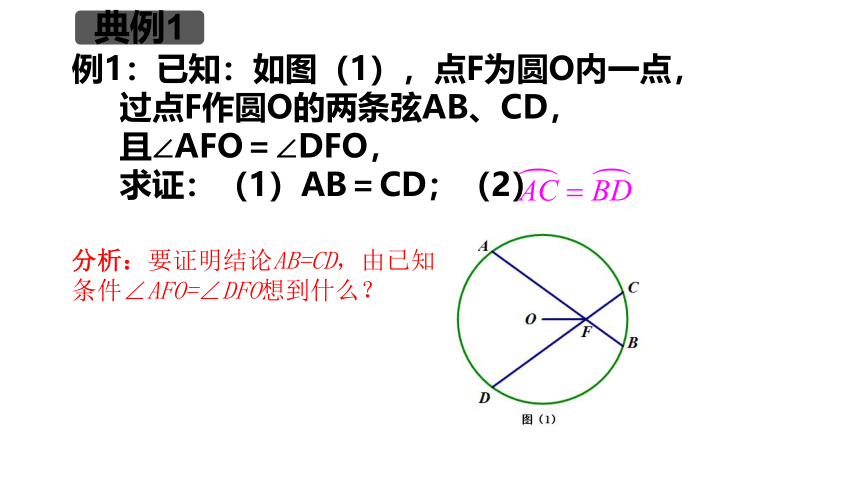
例1:已知:如图(1),点F为圆O内一点,
过点F作圆O的两条弦AB、CD,
且∠AFO=∠DFO,
求证:(1)AB=CD;(2)
分析:要证明结论AB=CD,由已知
条件∠AFO=∠DFO想到什么?
典例1
E
D
C
B
A
O
F
M
N
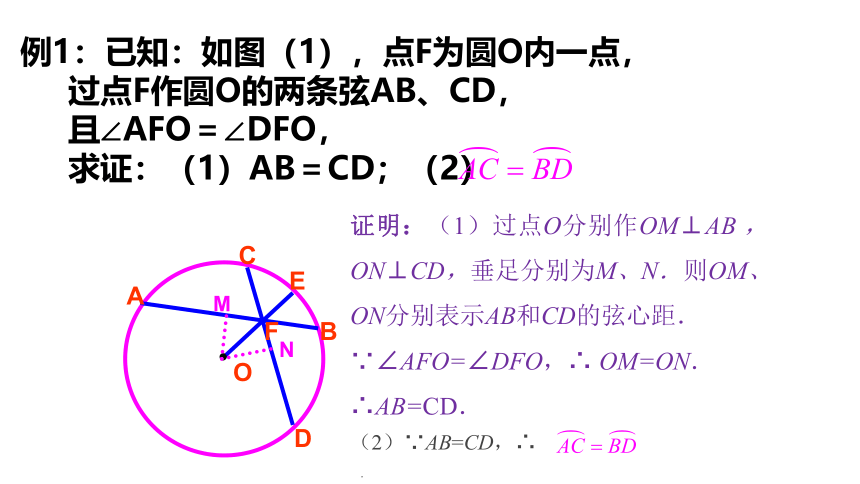
例1:已知:如图(1),点F为圆O内一点,
过点F作圆O的两条弦AB、CD,
且∠AFO=∠DFO,
求证:(1)AB=CD;(2)
证明:(1)过点O分别作OM⊥AB ,ON⊥CD,垂足分别为M、N.则OM、ON分别表示AB和CD的弦心距.
∵∠AFO=∠DFO,∴ OM=ON.
∴AB=CD.
(2)∵AB=CD,∴
.
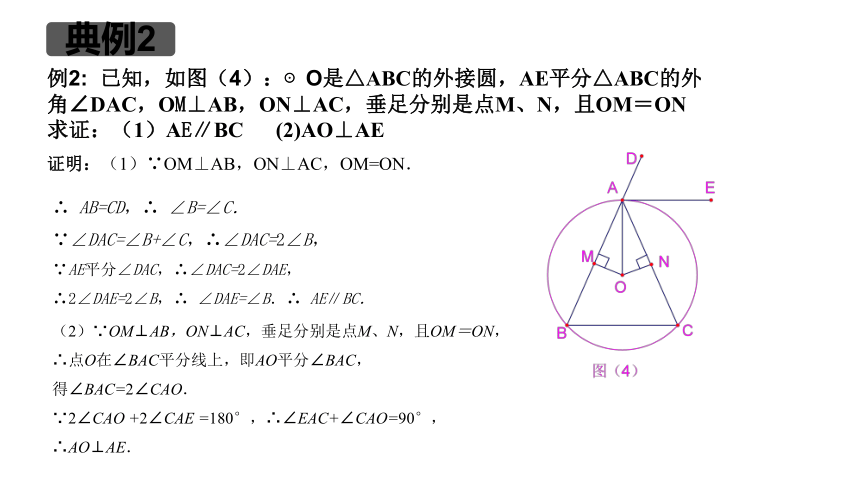
例2: 已知,如图(4):⊙O是△ABC的外接圆,AE平分△ABC的外角∠DAC,OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON
求证:(1)AE∥BC (2)AO⊥AE
证明:(1)∵OM⊥AB,ON⊥AC,OM=ON.
∴ AB=CD,∴ ∠B=∠C.
∵∠DAC=∠B+∠C,∴∠DAC=2∠B,
∵AE平分∠DAC,∴∠DAC=2∠DAE,
∴2∠DAE=2∠B,∴ ∠DAE=∠B.∴ AE∥BC.
(2)∵OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON,
∴点O在∠BAC平分线上,即AO平分∠BAC,
得∠BAC=2∠CAO.
∵2∠CAO +2∠CAE =180°,∴∠EAC+∠CAO=90°,
∴AO⊥AE.
典例2
课本练习
1.已知,在⊙O中,AB、CD是⊙O的弦,且AB=CD.
求证:△ACB≌△DBC.
2.已知,AB是 ⊙O的直径,AC和AD是分别位于AB两侧的两条相等的弦.
求证:AB平分∠CAD.
E
F
3.已知,⊙O的弦AB与CD相交于点E,AB=CD.
求证:AE=DE.
可证:△ABD≌△DCA
随堂检测
1.如果两个圆心角相等,那么 ( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
2.弦长等于半径的弦所对的圆心角等于 .
D
60 °
3.在同圆中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
⌒ ⌒
A
A. AB=2CD
⌒ ⌒
B. AB>CD
⌒ ⌒
C. AB⌒ ⌒
D. 不能确定
4.如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则BD的度数为( )
A.25°
B.30°
C.50°
D.65°
C
︵
5.如图,已知A、B、C、D是⊙O上的点,∠1=∠2,则下列结论中正确的有( )
①AB=CD;
②BD=AC;
③AC=BD;
④∠BOD=∠AOC.
A.1个 B.2个 C.3个 D.4个
︵
︵
︵
︵
D
B
6.在同圆或等圆中,不一定成立的是( )
A.相等的圆心角所对的弧相等
B.相等的弦所对的弧相等
C.相等的弧所对的弦相等
D.相等的弧所对的圆心角相等
7.如图,观察下列图形及相应推理,其中正确的是( )
A.①② B.③④ C.①③ D.②④
C
*8.如图,AB是⊙O的直径,若∠COA=∠DOB=60°,则与线段AO的长度相等的线段有( )
A.3条
B.4条
C.5条
D.6条
【点拨】∵∠COA=∠DOB=60°,∴∠COD=60°,∵OA=OC=OD=OB,∴△AOC,△COD,△BOD均为等边三角形,∴OA=OC=OD=OB=AC=CD=BD,故选D.
【答案】D
*9.在⊙O中,点M、N分别为弦AB、CD的中点,如果OM=ON,那么在结论:①AB=CD;②AB=CD;③∠AOB=∠COD中,正确的是( )
A.①② B.①③ C.②③ D.①②③
︵
︵
【点拨】∵点M、N分别是弦AB、CD的中点,∴OM⊥AB,ON⊥CD.
∵OM=ON,
∴AB=CD,AB=CD,∠AOB=∠COD.
【答案】D
︵
︵
10.如图,在⊙O中,弦AB>CD,OM⊥AB,ON⊥CD,点M、N分别为垂足,那么OM、ON的大小关系是( )
A.OM>ON
B.OM=ON
C.OMD.无法确定
错解:A或B
诊断:对于“在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都相等”这一性质中反映的各组量之间的关系判断不准,从而导致错误.
正解:C
圆心角
弦、弧、圆心角的关系定理
在同圆或等圆中
概念:顶点在圆心的角
应用提醒
①要注意前提条件;
②要灵活转化.
圆心角
相等
弦
相等
弧
相等
弦心距
相等
课堂小结
2022-2023学年九年级数学下册同步精品课堂(沪教版)
第 27 章 圆与正多边形
27.2圆心角、弧 弦、弦心距之间的关系(第3课时)
1.理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问
题.(重点)
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”
条件的意义.(难点)
学习目标
在同圆或等圆中,如果两个圆心角、两条劣弧(或优弧)、两条弦、两条弦的弦心距的四组量中有一组量相等,那么它们所对应的其余三组量也分别相等.
复习引入
在同圆或等圆中
题设
结论
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
复习引入
例1:已知:如图(1),点F为圆O内一点,
过点F作圆O的两条弦AB、CD,
且∠AFO=∠DFO,
求证:(1)AB=CD;(2)
分析:要证明结论AB=CD,由已知
条件∠AFO=∠DFO想到什么?
典例1
E
D
C
B
A
O
F
M
N
例1:已知:如图(1),点F为圆O内一点,
过点F作圆O的两条弦AB、CD,
且∠AFO=∠DFO,
求证:(1)AB=CD;(2)
证明:(1)过点O分别作OM⊥AB ,ON⊥CD,垂足分别为M、N.则OM、ON分别表示AB和CD的弦心距.
∵∠AFO=∠DFO,∴ OM=ON.
∴AB=CD.
(2)∵AB=CD,∴
.
例2: 已知,如图(4):⊙O是△ABC的外接圆,AE平分△ABC的外角∠DAC,OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON
求证:(1)AE∥BC (2)AO⊥AE
证明:(1)∵OM⊥AB,ON⊥AC,OM=ON.
∴ AB=CD,∴ ∠B=∠C.
∵∠DAC=∠B+∠C,∴∠DAC=2∠B,
∵AE平分∠DAC,∴∠DAC=2∠DAE,
∴2∠DAE=2∠B,∴ ∠DAE=∠B.∴ AE∥BC.
(2)∵OM⊥AB,ON⊥AC,垂足分别是点M、N,且OM=ON,
∴点O在∠BAC平分线上,即AO平分∠BAC,
得∠BAC=2∠CAO.
∵2∠CAO +2∠CAE =180°,∴∠EAC+∠CAO=90°,
∴AO⊥AE.
典例2
课本练习
1.已知,在⊙O中,AB、CD是⊙O的弦,且AB=CD.
求证:△ACB≌△DBC.
2.已知,AB是 ⊙O的直径,AC和AD是分别位于AB两侧的两条相等的弦.
求证:AB平分∠CAD.
E
F
3.已知,⊙O的弦AB与CD相交于点E,AB=CD.
求证:AE=DE.
可证:△ABD≌△DCA
随堂检测
1.如果两个圆心角相等,那么 ( )
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
2.弦长等于半径的弦所对的圆心角等于 .
D
60 °
3.在同圆中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
⌒ ⌒
A
A. AB=2CD
⌒ ⌒
B. AB>CD
⌒ ⌒
C. AB
D. 不能确定
4.如图,在△ABC中,∠C=90°,∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则BD的度数为( )
A.25°
B.30°
C.50°
D.65°
C
︵
5.如图,已知A、B、C、D是⊙O上的点,∠1=∠2,则下列结论中正确的有( )
①AB=CD;
②BD=AC;
③AC=BD;
④∠BOD=∠AOC.
A.1个 B.2个 C.3个 D.4个
︵
︵
︵
︵
D
B
6.在同圆或等圆中,不一定成立的是( )
A.相等的圆心角所对的弧相等
B.相等的弦所对的弧相等
C.相等的弧所对的弦相等
D.相等的弧所对的圆心角相等
7.如图,观察下列图形及相应推理,其中正确的是( )
A.①② B.③④ C.①③ D.②④
C
*8.如图,AB是⊙O的直径,若∠COA=∠DOB=60°,则与线段AO的长度相等的线段有( )
A.3条
B.4条
C.5条
D.6条
【点拨】∵∠COA=∠DOB=60°,∴∠COD=60°,∵OA=OC=OD=OB,∴△AOC,△COD,△BOD均为等边三角形,∴OA=OC=OD=OB=AC=CD=BD,故选D.
【答案】D
*9.在⊙O中,点M、N分别为弦AB、CD的中点,如果OM=ON,那么在结论:①AB=CD;②AB=CD;③∠AOB=∠COD中,正确的是( )
A.①② B.①③ C.②③ D.①②③
︵
︵
【点拨】∵点M、N分别是弦AB、CD的中点,∴OM⊥AB,ON⊥CD.
∵OM=ON,
∴AB=CD,AB=CD,∠AOB=∠COD.
【答案】D
︵
︵
10.如图,在⊙O中,弦AB>CD,OM⊥AB,ON⊥CD,点M、N分别为垂足,那么OM、ON的大小关系是( )
A.OM>ON
B.OM=ON
C.OM
错解:A或B
诊断:对于“在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都相等”这一性质中反映的各组量之间的关系判断不准,从而导致错误.
正解:C
圆心角
弦、弧、圆心角的关系定理
在同圆或等圆中
概念:顶点在圆心的角
应用提醒
①要注意前提条件;
②要灵活转化.
圆心角
相等
弦
相等
弧
相等
弦心距
相等
课堂小结
