27.2 圆心角、弧、弦、弦心距之间的关系(第2课时) 课件(共23张PPT)
文档属性
| 名称 | 27.2 圆心角、弧、弦、弦心距之间的关系(第2课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 08:15:58 | ||
图片预览




文档简介
(共23张PPT)
2022-2023学年九年级数学下册同步精品课堂(沪教版)
第 27 章 圆与正多边形
27.2圆心角、弧 弦、弦心距之间的关系(第2课时)
学习目标
1、掌握圆心角定义,理解并掌握圆心角,弧,弦,弦心距之间的关系
2、理解并掌握圆心角的度数与它所对的弧的度数之间的关系。
3、能利用圆心角、弧、弦、弦心距之间的关系解决有关的证明与计算问题。
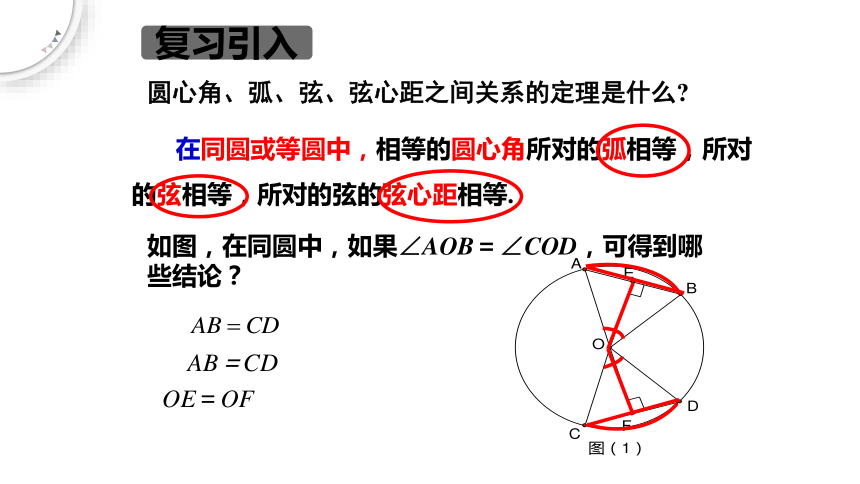
圆心角、弧、弦、弦心距之间关系的定理是什么
在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等,所对的弦的弦心距相等.
如图,在同圆中,如果∠AOB=∠COD,可得到哪些结论?
AB=CD
OE=OF
复习引入
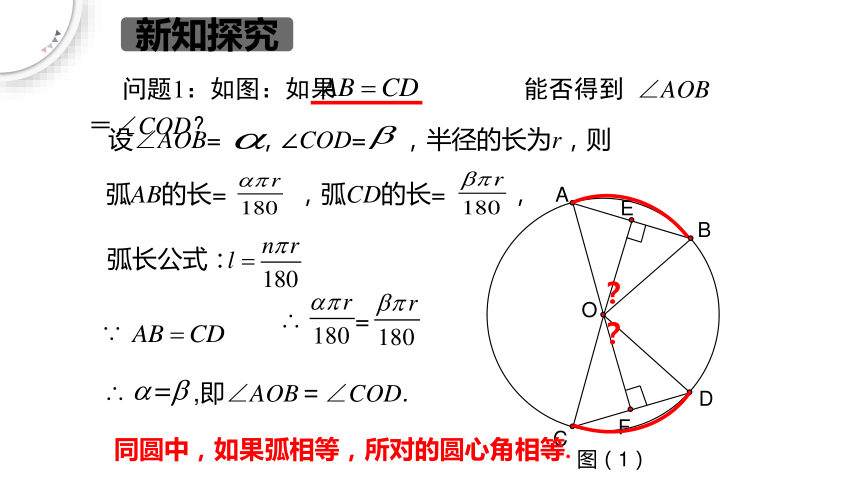
问题1:如图:如果 能否得到 ∠AOB=∠COD?
弧长公式:
设∠AOB= ,∠COD= ,半径的长为r,则
弧AB的长= ,弧CD的长= ,
∵
∴ =
∴ ,即∠AOB=∠COD.
?
?
同圆中,如果弧相等,所对的圆心角相等.
新知探究
问题2:如图,同圆中,若AB=CD,能否得到
∠AOB= ∠COD?
?
?
证明△OAB △OCD
由题意可得,半径OA=OB=OC=OD,
且AB=CD
则△AOB △COD,
∴∠AOB=∠COD
OA=OB=OC=OD
同圆中,如果弦相等,所对的圆心角相等.
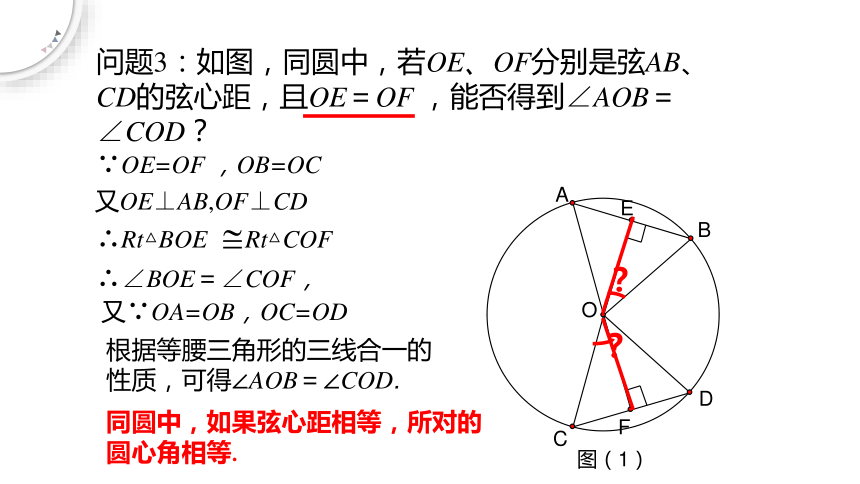
∵OE=OF ,OB=OC
问题3:如图,同圆中,若OE、OF分别是弦AB、CD的弦心距,且OE=OF ,能否得到∠AOB=∠COD?
?
?
又OE⊥AB,OF⊥CD
∴Rt△BOE Rt△COF
∴∠BOE=∠COF,
又∵OA=OB,OC=OD
根据等腰三角形的三线合一的性质,可得∠AOB=∠COD.
同圆中,如果弦心距相等,所对的圆心角相等.
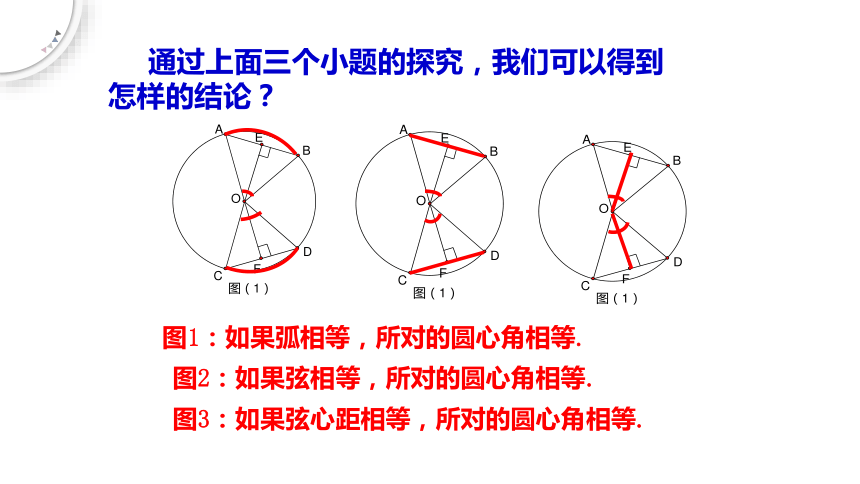
通过上面三个小题的探究,我们可以得到怎样的结论?
图1:如果弧相等,所对的圆心角相等.
图2:如果弦相等,所对的圆心角相等.
图3:如果弦心距相等,所对的圆心角相等.
圆心角、弧、弦、弦心距之间关系的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
在同圆或等圆中,
如果弧相等,弧所对的圆心角相等.
如果弦相等,弦所对的圆心角相等.
如果弦心距相等,弦心距所对弦的圆心角相等.
上面三个小题得到推论:
猜测圆心角、弧、弦、弦心距之间还存在哪些关系?
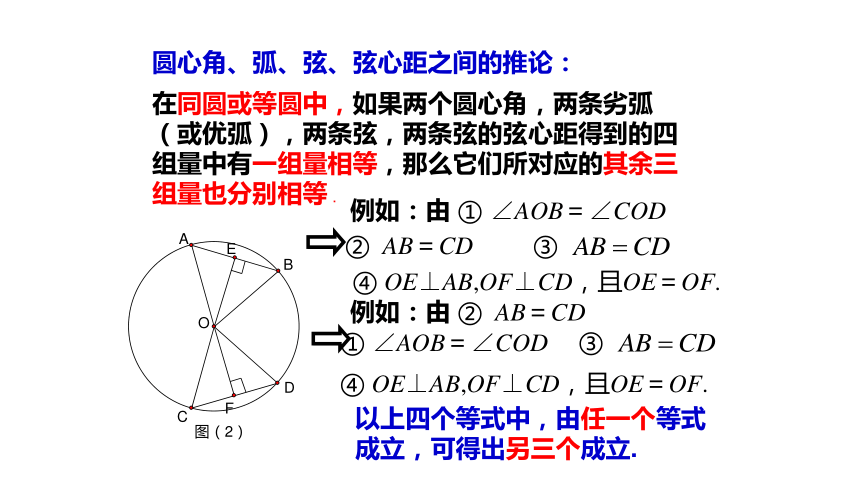
圆心角、弧、弦、弦心距之间的推论:
在同圆或等圆中,如果两个圆心角,两条劣弧(或优弧),两条弦,两条弦的弦心距得到的四组量中有一组量相等,那么它们所对应的其余三组量也分别相等 .
以上四个等式中,由任一个等式成立,可得出另三个成立.
例如:由 ① ∠AOB=∠COD
① ∠AOB=∠COD
② AB=CD
③
④ OE⊥AB,OF⊥CD,且OE=OF.
例如:由 ② AB=CD
③
④ OE⊥AB,OF⊥CD,且OE=OF.
例1: 如图(3),在⊙O中,弦AB、CD相交于E,OM、 ON分别是弦AB、CD的弦心距,如果OM=ON,求证: .
∵OM、ON分别是AB、CD的弦心距且OM=ON,
∴
即
∴
同圆或等圆上的两条弧,可像线段的和与差一样作出它们的和与差,并分别用“+”、“—”号表达
典例1
例2 已知:如图,在⊙O中, .AB、CD相交于点H.求证:(1)ΔABD≌ΔCDB;(2)OH平分∠AHC.
由推论得到什么?
弧相等所对的弦心距AD=CB
要证ABD≌ΔCDB
还有什么条件?
公共边BD
由已知条件还可以得到哪些?
即
由推论得AB=CD
证明:∵ ∴AD=BC,
即
得 AB=CD,
∵AD=CB,DB=BD,AB=CD,
∴ΔABD≌ΔCDB.
典例2
如何求EO=FO?
例2 已知:如图,在⊙O中, .AB、CD相交于点H.求证:(1)ΔABD≌ΔCDB;(2)OH平分∠AHC.
如何求证∠AHO=∠CHO?
利用角平分线性质定理的逆定理,作OE⊥AB、OF⊥CD , 如果EO=FO则∠AHO=∠CHO
由 得,OE=OF
证明:过点O作OE⊥AB、OF⊥CD,垂足分别为E、F,则OE、OF分别表示AB、CD的弦心距.
∵AB=CD
∴OE=OF
∴点O在∠AHC的平分线上,即OH平分∠AHC.
适时小结:
作弦心距是圆中的常添辅助线.
典例2
课本练习
1. 已知:如图,⊙O的弦AB与CD相较于点P,OM⊥AB,ON⊥DC,垂足分别是点M、N, 且 .
求证:OM=ON.
证明:∵
∴
∴
∵OM⊥AB,ON⊥DC,
∴OM=ON.
用到弦心距的时候,一定要指明垂直.
2 .已知:如图,AB、CE是⊙O的直径,CD是⊙O的弦,CD∥AB. 求证:
证明:连接OD
∵∠AOC=∠EOB,
∴ .
∵OC=OD
∴∠C=∠D,
∵CD∥AB,
∵∠EOB=∠OCD,∠BOD=∠ODC,
∴∠EOB=∠BOD,
∴ .
∴ .
适时小结: 添加半径也是圆中常添的辅助线
3.已知:如图,AD、BC是⊙O的弦,AD=BC,OM,ON分别表示弦AB和CD的弦心距.
求证:OM=ON.
证明:∵AD=BC,
∴
∴
∴
∵OM,ON分别表示弦AB和CD的弦心距,
∴OM=ON.
随堂检测
⌒
解:连接OE,如图.
∴∠COE=40°,
∵CE∥AB,
∴∠BOD=∠C=70°.
∵CE为40°,
⌒
1.如图,AB,CD为⊙O的两条直径,CE为⊙O的弦,且CE // AB,CE为40°,求∠ BOD的度数.
O
C
E
A
B
D
2.如图,已知AB、CD为⊙O的两条弦,AD=BC.
求证:AB=CD.
⌒ ⌒
.
C
A
B
D
O
3. 如图,AB是☉O的直径,点C在上,∠AOC=40°,D是BC的中点,求∠OCD的度数.
⌒
解:连接OD.
∵AB是☉O的直径,∠AOC=40°,
∴∠BOC=140°.
∵D是BC的中点,
∴∠COD=∠BOD= ∠BOC=70°,
∵OC=OD,
∴∠OCD=∠ODC= (180°-∠COD)=55°
⌒
4.已知:如图2,AB、CD是⊙O的弦,且AB与CD不平行,M、N分别是AB、CD的中点,AB=CD,那么∠AMN与∠CNM的大小关系是什么?为什么?
解:连结OM、ON,
∵M、N分别为弦AB、CD的中点,
∴∠AMO=∠CNO=90°
∵ AB=CD
∴ OM=ON
∴∠OMN=∠CNM
∴∠AMN=∠CNM
5. 已知:如图,点O是∠ A平分线上的一点,
⊙O分别交∠ A两边于点C,D和点 E,F.
求证:CD=EF.
证明 过点O作OK ⊥ CD、 OK ′ ⊥EF,垂足分别为K,K ′ .
O
A
D
E
F
C
H
K
∴ OK = OK ′ (角平分线性质),
∴ CD =EF.
弦心距相等
弦相等
以上四个等式中,由任一个等式成立,可得出另三个成立.
例如:由 ① ∠AOB=∠COD
① ∠AOB=∠COD
② AB=CD
③
④ OE⊥AB,OF⊥CD,且OE=OF.
例如:由 ② AB=CD
③
④ OE⊥AB,OF⊥CD,且OE=OF.
1、圆心角、弧、弦、弦心距之间的推论:
2、常添辅助线的方法有:
作弦心距、添加半径
课堂小结
2022-2023学年九年级数学下册同步精品课堂(沪教版)
第 27 章 圆与正多边形
27.2圆心角、弧 弦、弦心距之间的关系(第2课时)
学习目标
1、掌握圆心角定义,理解并掌握圆心角,弧,弦,弦心距之间的关系
2、理解并掌握圆心角的度数与它所对的弧的度数之间的关系。
3、能利用圆心角、弧、弦、弦心距之间的关系解决有关的证明与计算问题。
圆心角、弧、弦、弦心距之间关系的定理是什么
在同圆或等圆中,相等的圆心角所对的弧相等,所对
的弦相等,所对的弦的弦心距相等.
如图,在同圆中,如果∠AOB=∠COD,可得到哪些结论?
AB=CD
OE=OF
复习引入
问题1:如图:如果 能否得到 ∠AOB=∠COD?
弧长公式:
设∠AOB= ,∠COD= ,半径的长为r,则
弧AB的长= ,弧CD的长= ,
∵
∴ =
∴ ,即∠AOB=∠COD.
?
?
同圆中,如果弧相等,所对的圆心角相等.
新知探究
问题2:如图,同圆中,若AB=CD,能否得到
∠AOB= ∠COD?
?
?
证明△OAB △OCD
由题意可得,半径OA=OB=OC=OD,
且AB=CD
则△AOB △COD,
∴∠AOB=∠COD
OA=OB=OC=OD
同圆中,如果弦相等,所对的圆心角相等.
∵OE=OF ,OB=OC
问题3:如图,同圆中,若OE、OF分别是弦AB、CD的弦心距,且OE=OF ,能否得到∠AOB=∠COD?
?
?
又OE⊥AB,OF⊥CD
∴Rt△BOE Rt△COF
∴∠BOE=∠COF,
又∵OA=OB,OC=OD
根据等腰三角形的三线合一的性质,可得∠AOB=∠COD.
同圆中,如果弦心距相等,所对的圆心角相等.
通过上面三个小题的探究,我们可以得到怎样的结论?
图1:如果弧相等,所对的圆心角相等.
图2:如果弦相等,所对的圆心角相等.
图3:如果弦心距相等,所对的圆心角相等.
圆心角、弧、弦、弦心距之间关系的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
在同圆或等圆中,
如果弧相等,弧所对的圆心角相等.
如果弦相等,弦所对的圆心角相等.
如果弦心距相等,弦心距所对弦的圆心角相等.
上面三个小题得到推论:
猜测圆心角、弧、弦、弦心距之间还存在哪些关系?
圆心角、弧、弦、弦心距之间的推论:
在同圆或等圆中,如果两个圆心角,两条劣弧(或优弧),两条弦,两条弦的弦心距得到的四组量中有一组量相等,那么它们所对应的其余三组量也分别相等 .
以上四个等式中,由任一个等式成立,可得出另三个成立.
例如:由 ① ∠AOB=∠COD
① ∠AOB=∠COD
② AB=CD
③
④ OE⊥AB,OF⊥CD,且OE=OF.
例如:由 ② AB=CD
③
④ OE⊥AB,OF⊥CD,且OE=OF.
例1: 如图(3),在⊙O中,弦AB、CD相交于E,OM、 ON分别是弦AB、CD的弦心距,如果OM=ON,求证: .
∵OM、ON分别是AB、CD的弦心距且OM=ON,
∴
即
∴
同圆或等圆上的两条弧,可像线段的和与差一样作出它们的和与差,并分别用“+”、“—”号表达
典例1
例2 已知:如图,在⊙O中, .AB、CD相交于点H.求证:(1)ΔABD≌ΔCDB;(2)OH平分∠AHC.
由推论得到什么?
弧相等所对的弦心距AD=CB
要证ABD≌ΔCDB
还有什么条件?
公共边BD
由已知条件还可以得到哪些?
即
由推论得AB=CD
证明:∵ ∴AD=BC,
即
得 AB=CD,
∵AD=CB,DB=BD,AB=CD,
∴ΔABD≌ΔCDB.
典例2
如何求EO=FO?
例2 已知:如图,在⊙O中, .AB、CD相交于点H.求证:(1)ΔABD≌ΔCDB;(2)OH平分∠AHC.
如何求证∠AHO=∠CHO?
利用角平分线性质定理的逆定理,作OE⊥AB、OF⊥CD , 如果EO=FO则∠AHO=∠CHO
由 得,OE=OF
证明:过点O作OE⊥AB、OF⊥CD,垂足分别为E、F,则OE、OF分别表示AB、CD的弦心距.
∵AB=CD
∴OE=OF
∴点O在∠AHC的平分线上,即OH平分∠AHC.
适时小结:
作弦心距是圆中的常添辅助线.
典例2
课本练习
1. 已知:如图,⊙O的弦AB与CD相较于点P,OM⊥AB,ON⊥DC,垂足分别是点M、N, 且 .
求证:OM=ON.
证明:∵
∴
∴
∵OM⊥AB,ON⊥DC,
∴OM=ON.
用到弦心距的时候,一定要指明垂直.
2 .已知:如图,AB、CE是⊙O的直径,CD是⊙O的弦,CD∥AB. 求证:
证明:连接OD
∵∠AOC=∠EOB,
∴ .
∵OC=OD
∴∠C=∠D,
∵CD∥AB,
∵∠EOB=∠OCD,∠BOD=∠ODC,
∴∠EOB=∠BOD,
∴ .
∴ .
适时小结: 添加半径也是圆中常添的辅助线
3.已知:如图,AD、BC是⊙O的弦,AD=BC,OM,ON分别表示弦AB和CD的弦心距.
求证:OM=ON.
证明:∵AD=BC,
∴
∴
∴
∵OM,ON分别表示弦AB和CD的弦心距,
∴OM=ON.
随堂检测
⌒
解:连接OE,如图.
∴∠COE=40°,
∵CE∥AB,
∴∠BOD=∠C=70°.
∵CE为40°,
⌒
1.如图,AB,CD为⊙O的两条直径,CE为⊙O的弦,且CE // AB,CE为40°,求∠ BOD的度数.
O
C
E
A
B
D
2.如图,已知AB、CD为⊙O的两条弦,AD=BC.
求证:AB=CD.
⌒ ⌒
.
C
A
B
D
O
3. 如图,AB是☉O的直径,点C在上,∠AOC=40°,D是BC的中点,求∠OCD的度数.
⌒
解:连接OD.
∵AB是☉O的直径,∠AOC=40°,
∴∠BOC=140°.
∵D是BC的中点,
∴∠COD=∠BOD= ∠BOC=70°,
∵OC=OD,
∴∠OCD=∠ODC= (180°-∠COD)=55°
⌒
4.已知:如图2,AB、CD是⊙O的弦,且AB与CD不平行,M、N分别是AB、CD的中点,AB=CD,那么∠AMN与∠CNM的大小关系是什么?为什么?
解:连结OM、ON,
∵M、N分别为弦AB、CD的中点,
∴∠AMO=∠CNO=90°
∵ AB=CD
∴ OM=ON
∴∠OMN=∠CNM
∴∠AMN=∠CNM
5. 已知:如图,点O是∠ A平分线上的一点,
⊙O分别交∠ A两边于点C,D和点 E,F.
求证:CD=EF.
证明 过点O作OK ⊥ CD、 OK ′ ⊥EF,垂足分别为K,K ′ .
O
A
D
E
F
C
H
K
∴ OK = OK ′ (角平分线性质),
∴ CD =EF.
弦心距相等
弦相等
以上四个等式中,由任一个等式成立,可得出另三个成立.
例如:由 ① ∠AOB=∠COD
① ∠AOB=∠COD
② AB=CD
③
④ OE⊥AB,OF⊥CD,且OE=OF.
例如:由 ② AB=CD
③
④ OE⊥AB,OF⊥CD,且OE=OF.
1、圆心角、弧、弦、弦心距之间的推论:
2、常添辅助线的方法有:
作弦心距、添加半径
课堂小结
