1.5 三角函数的应用 课件(共38张PPT)
文档属性
| 名称 | 1.5 三角函数的应用 课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 08:17:09 | ||
图片预览








文档简介
(共38张PPT)
第一章 直角三角形的边角关系
1.5 三角函数的应用
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握方位角的概念,学会方位角的表示;
2、掌握仰角、俯角的概念,并且由仰角、俯角求出长度;
3、学会运用三角函数值求出仰角、俯角和方位角的问题;
导入新课
观察与思考
中国人民解放军海军福建舰(舷号:18,简称福建舰),是中国完全自主设计建造的首艘弹射型航空母舰,采用平直通长飞行甲板,配置电磁弹射和阻拦装置,满载排水量8万余吨。
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
画出方向图(表示东南西北四个方向的)并依次画出表示东南方向、西北方向、北偏东65度、南偏东34度方向的射线.
试一试:
讲授新课
知识点一 与方位角有关的实际问题
引例 如图,海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处。之后,货轮继续向东航行.货轮继续航行会有触礁的危险吗?
B
A
C
60°
D
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于 10 n mile.
北
东
解:由点A作AD⊥BC于点D,
设AD= x ,
则在Rt△ABD中,
在Rt△ACD中,
解得
所以,这船继续向东航行是安全的.
B
A
C
D
25°
55°
北
东
由BC=BD-CD,得
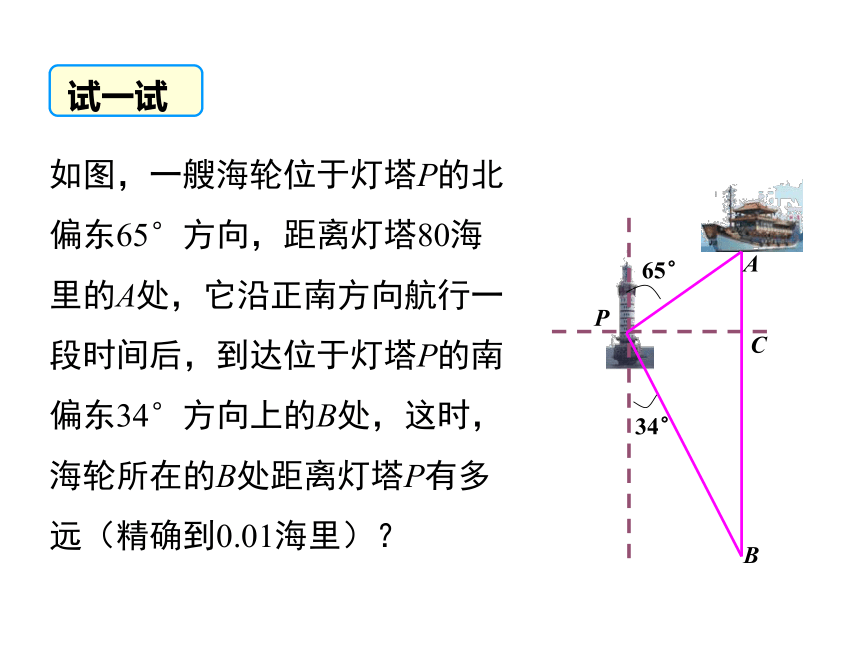
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
65°
34°
P
B
C
A
试一试
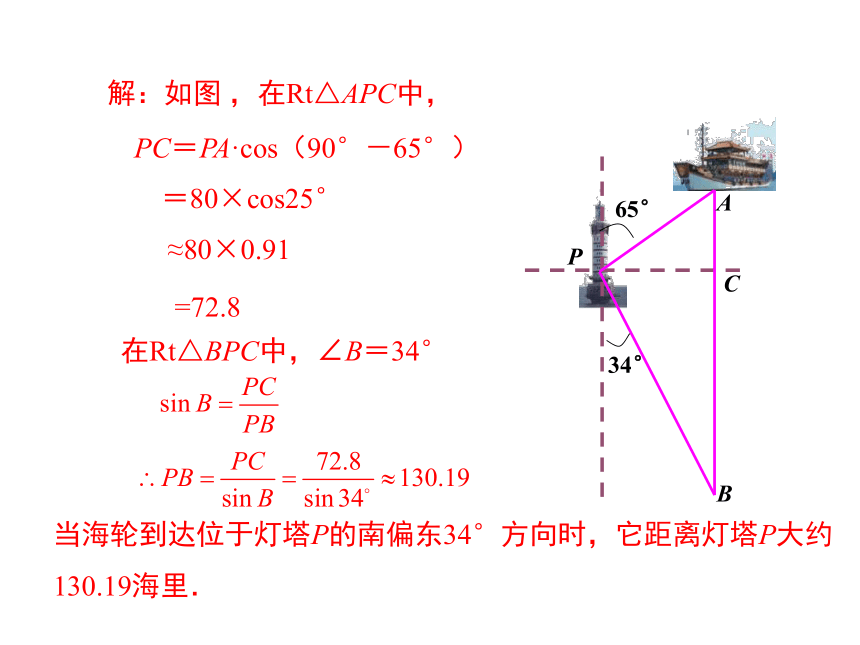
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.8
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.19海里.
65°
34°
P
B
C
A
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
方法归纳
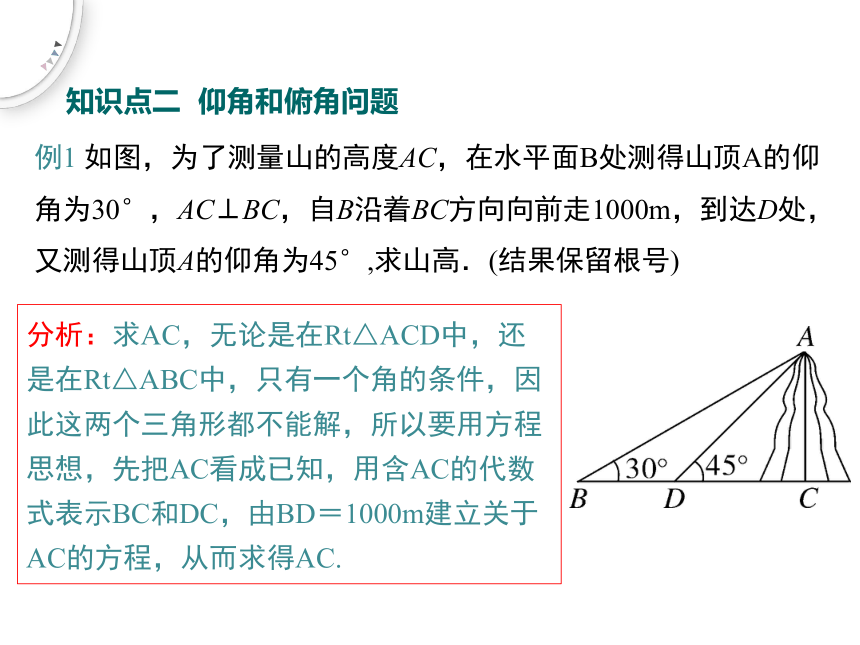
知识点二 仰角和俯角问题
例1 如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)
分析:求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解,所以要用方程思想,先把AC看成已知,用含AC的代数式表示BC和DC,由BD=1000m建立关于AC的方程,从而求得AC.
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
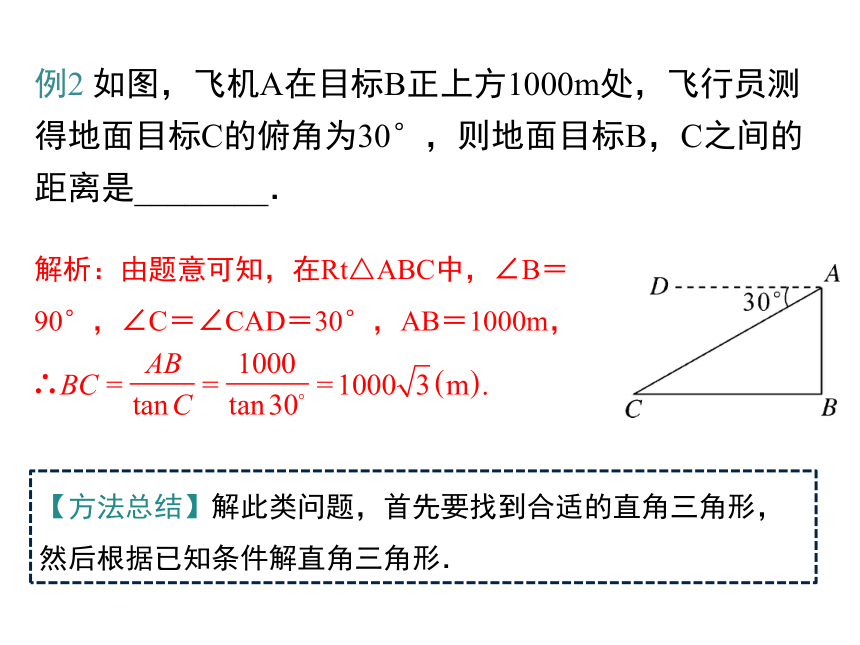
例2 如图,飞机A在目标B正上方1000m处,飞行员测得地面目标C的俯角为30°,则地面目标B,C之间的距离是________.
解析:由题意可知,在Rt△ABC中,∠B=90°,∠C=∠CAD=30°,AB=1000m,
【方法总结】解此类问题,首先要找到合适的直角三角形,然后根据已知条件解直角三角形.
例3 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,
α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
解:在等腰三角形BCD中∠ACD=90°,
BC=DC=40m.
在Rt△ACD中,
∴AB=AC-BC=55.2-40=15.1
答:旗杆的高度为15.1m.
练一练
知识点三 利用坡角解决问题
例4.水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度为1∶3,斜坡CD的坡度为1∶2.5,求:
(1)坝底AD与斜坡AB的长度(精确到0.1m );
(2)斜坡CD的坡角α(精确到 1°).
E
F
A
D
B
C
1:2.5
23
6
α
解:(1)分别过点B、C作BE⊥AD,CF⊥AD,垂足分别为点E、 F,由题意可知
BE=CF=23m , EF=BC=6m.
E
F
A
D
B
C
1:2.5
23
6
α
在Rt△ABE中
在Rt△DCF中,同理可得
=69+6+57.5=132.5m
在Rt△ABE中,由勾股定理可得
(2) 斜坡CD的坡度为tanα=1:2.5=0.4,
由计算器可算得
答:坝底宽AD为132.5米,斜坡AB的长约为72.7米.斜坡CD的坡角α约为22°.
当堂练习
1.如图,一架人字梯,若AB=AC,梯子离地面的垂直距离AD为2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.2tanα米 B.米 C.4tanα米 D.米
【答案】D
【详解】解:过点A作,如图所示:
∵AB=AC,AD⊥BC,
∴BD=DC,
∵tanα=,
∴DC=米,
∴BC=2DC=米,故D正确.
故选:D.
2.如图,传送带和地面所成斜坡的坡度为1:3,若它把物体从地面点A处送到离地面2米高的B处,则物体从A到B所经过的路程为( )
A.6米 B.米 C.2米 D. 3米
【答案】C
【详解】解:过点B作BC⊥AC于点C,
∵传送带和地面所成斜坡的坡度为1:3,
∴ ,
∴AC=6米,
在Rt△ABC中,∠ACB=90°,由勾股定理即可得到AB=2米 ,
故选:C.
3.如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为多少米(结果保留根号).( )
A.200米B.300米C.(100+100)米 D.(100+)米
【答案】C
【详解】解:∵∠MCA=45°,∠NVB=30°,MN∥AB,
∴∠A=45°,∠B=30°,
∵CD=100米,CD⊥AB,
∴AD=CD=100米,DB=(米),
∴AB=AD+DB=(100+100)米.
故选:C.
4.某游乐场一个不等臂跷跷板AB长 5.6 米,支撑柱 OH 垂直地面,如图 1,当 AB的一端A着地时,AB与地面的夹角的正切值为;如图2,当AB 的另一端 B 着地时,AB 与地面夹角的正弦值为,则支撑柱 OH的长为( )
A.0.4 米 B.0.8 米 C.米 D.1.2 米
【答案】D
【分析】根据正弦的定义得到OH=OA,OB=3OH,根据题意列式计算即可.
【点睛】本题考查的是解直角三角形的应用—坡度坡角问题,掌握坡度的概念、熟记锐角三角函数的定义是解题的关键.
5.小丽想测量学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为30°,测倾器到旗杆底部的距离AD为12米,测倾器的高度AB为1.6米,那么旗杆的高度CD为__________米(结果保留根号).
【答案】
【分析】根据已知条件和tan∠CBE的值求出CE,即可求解.
6.如图,在高度是18米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的仰角为45°,则这个建筑物的高度CD=__________米(结果可保留根号);
【答案】18+6
【分析】作AE⊥CD于点E,则△AED和△ABD都是等腰直角三角形,即可求得DE的长,然后在直角三角形中国利用三角函数求得CE的长,进而求得CD的长.
7.如图,小明在骑行过程中发现山上有一建筑物,他测得仰角为15°;沿水平笔直的公路向建筑物的方向行驶4千米后,测得该建筑物的仰角为30°,若小明的眼睛与地面的距离忽略不计,则该建筑物离地面的高度为___________千米.
【答案】2
【答案】2
【分析】过该建筑物的顶端点C作CD⊥AB,交AB的延长线于点D,可得∠ACB=∠CBD-∠CAB=15°,即∠ACB=∠CAB,则BC=AB=4千米,在Rt△BCD中,sin30°=,即可求得CD.
8.如图,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.请你根据图中数据计算回答,请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?_____.(填是或否)(可能用到的参考数值:sin27°=0.45,cos27°=0.89,tan27°=0.51)
【答案】否
【详解】解:根据天花板与地面平行,可知∠CAB=27°,
CB=AC·tan∠CAB=4×0.51=2.04(米).
因为2.04>1.78,
所以小敏不会有碰头危险.
故答案为:否.
9.长泰大桥是长春市最高的双塔斜拉式高架桥,大桥属于双塔双索面混凝土特大斜拉桥桥型,图①是大桥的实物图,图②是大桥的示意图.假设你站在桥上点A处测得拉索AB与水平桥面的夹角是39°,点A处距离大桥立柱CD底端D的距离AD为97米,已知大桥立柱上B点距立柱顶端C点的距离BC为5米,求大桥立柱CD的高.(结果精确到1米)参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81
【详解】解:在Rt△ABD中,∠BAD=39°,AD=97米,
∴BD=AD·tan97°≈97×0.81≈78.57(米),
∵BC=5米,
∴CD=BC+BD=5+78.57≈84(米)
∴大桥立柱CD的高约为84米.
10.图1是停车场入口处的升降杆,当汽车刷牌照进入时,升降杆就会从水平位置升起.图2是其示意图,其中BE∥CD,BC⊥CD,ED⊥CD,AB=CD=3.3m,BC=1m,现由于故障,AB不能完全升起,∠ABE最大为42°.
(1)求故障时A点最高可距离地面多少m(精确到0.1m).
(2)若一辆箱式小货车宽1.8m,高2.4m,请问这辆车能否在升降杆故障时进入停车场?
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
【详解】(1)解:过点A作AF⊥BE于点F,则∠AFB=90°,
当故障时A点最高时,∠ABF=42°,
在Rt△ABF中,sin42°=,即0.67=,
∴AF=2.211m,
∴此时A点离地面长为:2.211+1≈3.3m;
(2)解:在CD上取点H,使得DH=1.8m,过点H作HG⊥CD,交AB于点G,交BE于点M,
则HM=BC=1m,CH=BM=3.3-1.8=1.5m,
在Rt△BMG中,tan42°=,即0.9=,
∴GM=1.35m,
∴GH=GM+MH=1.35+1=2.35<2.4m,
即小货车不能在升降杆故障时进入停车场
课堂小结
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(作垂直,使之变成直角三角形,可以运用三角函数值);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)通过三角函数值解出三角形,得到数学意义上的答案;
(4)根据实际情况,得到符合条件的答案.
第一章 直角三角形的边角关系
1.5 三角函数的应用
北师大版九年级下册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握方位角的概念,学会方位角的表示;
2、掌握仰角、俯角的概念,并且由仰角、俯角求出长度;
3、学会运用三角函数值求出仰角、俯角和方位角的问题;
导入新课
观察与思考
中国人民解放军海军福建舰(舷号:18,简称福建舰),是中国完全自主设计建造的首艘弹射型航空母舰,采用平直通长飞行甲板,配置电磁弹射和阻拦装置,满载排水量8万余吨。
那你知道如何结合方位角等数据进行计算,帮助轮船在航行中远离危险吗?
画出方向图(表示东南西北四个方向的)并依次画出表示东南方向、西北方向、北偏东65度、南偏东34度方向的射线.
试一试:
讲授新课
知识点一 与方位角有关的实际问题
引例 如图,海中有一个小岛A,该岛四周10n mile内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20n mile后到达该岛的南偏西25°的C处。之后,货轮继续向东航行.货轮继续航行会有触礁的危险吗?
B
A
C
60°
D
【分析】这船继续向东航行是否安全,取决于灯塔C到AB航线的距离是否大于 10 n mile.
北
东
解:由点A作AD⊥BC于点D,
设AD= x ,
则在Rt△ABD中,
在Rt△ACD中,
解得
所以,这船继续向东航行是安全的.
B
A
C
D
25°
55°
北
东
由BC=BD-CD,得
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
65°
34°
P
B
C
A
试一试
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈80×0.91
=72.8
在Rt△BPC中,∠B=34°
当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130.19海里.
65°
34°
P
B
C
A
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
方法归纳
知识点二 仰角和俯角问题
例1 如图,为了测量山的高度AC,在水平面B处测得山顶A的仰角为30°,AC⊥BC,自B沿着BC方向向前走1000m,到达D处,又测得山顶A的仰角为45°,求山高.(结果保留根号)
分析:求AC,无论是在Rt△ACD中,还是在Rt△ABC中,只有一个角的条件,因此这两个三角形都不能解,所以要用方程思想,先把AC看成已知,用含AC的代数式表示BC和DC,由BD=1000m建立关于AC的方程,从而求得AC.
解:在Rt△ABC中,
在Rt△ACD中,
∴BD=BC-DC
例2 如图,飞机A在目标B正上方1000m处,飞行员测得地面目标C的俯角为30°,则地面目标B,C之间的距离是________.
解析:由题意可知,在Rt△ABC中,∠B=90°,∠C=∠CAD=30°,AB=1000m,
【方法总结】解此类问题,首先要找到合适的直角三角形,然后根据已知条件解直角三角形.
例3 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°.Rt△ABD中,
α=30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
解:如图,α = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
A
B
C
D
40m
54°
45°
A
B
C
D
40m
54°
45°
解:在等腰三角形BCD中∠ACD=90°,
BC=DC=40m.
在Rt△ACD中,
∴AB=AC-BC=55.2-40=15.1
答:旗杆的高度为15.1m.
练一练
知识点三 利用坡角解决问题
例4.水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度为1∶3,斜坡CD的坡度为1∶2.5,求:
(1)坝底AD与斜坡AB的长度(精确到0.1m );
(2)斜坡CD的坡角α(精确到 1°).
E
F
A
D
B
C
1:2.5
23
6
α
解:(1)分别过点B、C作BE⊥AD,CF⊥AD,垂足分别为点E、 F,由题意可知
BE=CF=23m , EF=BC=6m.
E
F
A
D
B
C
1:2.5
23
6
α
在Rt△ABE中
在Rt△DCF中,同理可得
=69+6+57.5=132.5m
在Rt△ABE中,由勾股定理可得
(2) 斜坡CD的坡度为tanα=1:2.5=0.4,
由计算器可算得
答:坝底宽AD为132.5米,斜坡AB的长约为72.7米.斜坡CD的坡角α约为22°.
当堂练习
1.如图,一架人字梯,若AB=AC,梯子离地面的垂直距离AD为2米,AC与地面BC的夹角为α,则两梯脚之间的距离BC为( )
A.2tanα米 B.米 C.4tanα米 D.米
【答案】D
【详解】解:过点A作,如图所示:
∵AB=AC,AD⊥BC,
∴BD=DC,
∵tanα=,
∴DC=米,
∴BC=2DC=米,故D正确.
故选:D.
2.如图,传送带和地面所成斜坡的坡度为1:3,若它把物体从地面点A处送到离地面2米高的B处,则物体从A到B所经过的路程为( )
A.6米 B.米 C.2米 D. 3米
【答案】C
【详解】解:过点B作BC⊥AC于点C,
∵传送带和地面所成斜坡的坡度为1:3,
∴ ,
∴AC=6米,
在Rt△ABC中,∠ACB=90°,由勾股定理即可得到AB=2米 ,
故选:C.
3.如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为多少米(结果保留根号).( )
A.200米B.300米C.(100+100)米 D.(100+)米
【答案】C
【详解】解:∵∠MCA=45°,∠NVB=30°,MN∥AB,
∴∠A=45°,∠B=30°,
∵CD=100米,CD⊥AB,
∴AD=CD=100米,DB=(米),
∴AB=AD+DB=(100+100)米.
故选:C.
4.某游乐场一个不等臂跷跷板AB长 5.6 米,支撑柱 OH 垂直地面,如图 1,当 AB的一端A着地时,AB与地面的夹角的正切值为;如图2,当AB 的另一端 B 着地时,AB 与地面夹角的正弦值为,则支撑柱 OH的长为( )
A.0.4 米 B.0.8 米 C.米 D.1.2 米
【答案】D
【分析】根据正弦的定义得到OH=OA,OB=3OH,根据题意列式计算即可.
【点睛】本题考查的是解直角三角形的应用—坡度坡角问题,掌握坡度的概念、熟记锐角三角函数的定义是解题的关键.
5.小丽想测量学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为30°,测倾器到旗杆底部的距离AD为12米,测倾器的高度AB为1.6米,那么旗杆的高度CD为__________米(结果保留根号).
【答案】
【分析】根据已知条件和tan∠CBE的值求出CE,即可求解.
6.如图,在高度是18米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的仰角为45°,则这个建筑物的高度CD=__________米(结果可保留根号);
【答案】18+6
【分析】作AE⊥CD于点E,则△AED和△ABD都是等腰直角三角形,即可求得DE的长,然后在直角三角形中国利用三角函数求得CE的长,进而求得CD的长.
7.如图,小明在骑行过程中发现山上有一建筑物,他测得仰角为15°;沿水平笔直的公路向建筑物的方向行驶4千米后,测得该建筑物的仰角为30°,若小明的眼睛与地面的距离忽略不计,则该建筑物离地面的高度为___________千米.
【答案】2
【答案】2
【分析】过该建筑物的顶端点C作CD⊥AB,交AB的延长线于点D,可得∠ACB=∠CBD-∠CAB=15°,即∠ACB=∠CAB,则BC=AB=4千米,在Rt△BCD中,sin30°=,即可求得CD.
8.如图,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.请你根据图中数据计算回答,请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?_____.(填是或否)(可能用到的参考数值:sin27°=0.45,cos27°=0.89,tan27°=0.51)
【答案】否
【详解】解:根据天花板与地面平行,可知∠CAB=27°,
CB=AC·tan∠CAB=4×0.51=2.04(米).
因为2.04>1.78,
所以小敏不会有碰头危险.
故答案为:否.
9.长泰大桥是长春市最高的双塔斜拉式高架桥,大桥属于双塔双索面混凝土特大斜拉桥桥型,图①是大桥的实物图,图②是大桥的示意图.假设你站在桥上点A处测得拉索AB与水平桥面的夹角是39°,点A处距离大桥立柱CD底端D的距离AD为97米,已知大桥立柱上B点距立柱顶端C点的距离BC为5米,求大桥立柱CD的高.(结果精确到1米)参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81
【详解】解:在Rt△ABD中,∠BAD=39°,AD=97米,
∴BD=AD·tan97°≈97×0.81≈78.57(米),
∵BC=5米,
∴CD=BC+BD=5+78.57≈84(米)
∴大桥立柱CD的高约为84米.
10.图1是停车场入口处的升降杆,当汽车刷牌照进入时,升降杆就会从水平位置升起.图2是其示意图,其中BE∥CD,BC⊥CD,ED⊥CD,AB=CD=3.3m,BC=1m,现由于故障,AB不能完全升起,∠ABE最大为42°.
(1)求故障时A点最高可距离地面多少m(精确到0.1m).
(2)若一辆箱式小货车宽1.8m,高2.4m,请问这辆车能否在升降杆故障时进入停车场?
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
【详解】(1)解:过点A作AF⊥BE于点F,则∠AFB=90°,
当故障时A点最高时,∠ABF=42°,
在Rt△ABF中,sin42°=,即0.67=,
∴AF=2.211m,
∴此时A点离地面长为:2.211+1≈3.3m;
(2)解:在CD上取点H,使得DH=1.8m,过点H作HG⊥CD,交AB于点G,交BE于点M,
则HM=BC=1m,CH=BM=3.3-1.8=1.5m,
在Rt△BMG中,tan42°=,即0.9=,
∴GM=1.35m,
∴GH=GM+MH=1.35+1=2.35<2.4m,
即小货车不能在升降杆故障时进入停车场
课堂小结
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(作垂直,使之变成直角三角形,可以运用三角函数值);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)通过三角函数值解出三角形,得到数学意义上的答案;
(4)根据实际情况,得到符合条件的答案.
