2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列前n项和公式第二课时 课件(共23张PPT)
文档属性
| 名称 | 2022-2023学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列前n项和公式第二课时 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 838.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 07:15:07 | ||
图片预览








文档简介
(共23张PPT)
等差数列的前n项和
的性质及应用
等差数列的前n项和公式:
形式1:
形式2:
复习回顾
S n与
之间的关系:
当n = 1时,
当n ≥ 2时,
1.将等差数列前n项和公式
看作是一个关于n的函数,这个函数有什么特点?
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
令
A
B
等差数列的前n项的最值问题
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法1
由S3=S11得
∴ d=-2
∴当n=7时,Sn取最大值49.
7
n
11
3
Sn
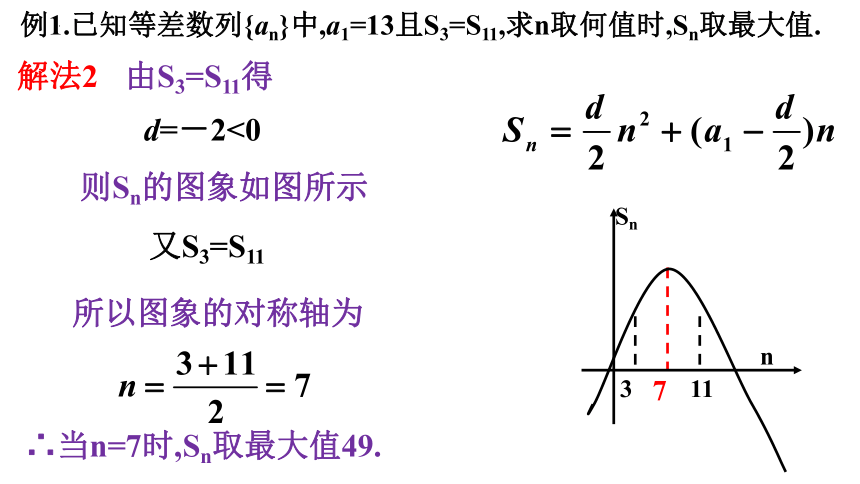
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法2
由S3=S11得
d=-2<0
∴当n=7时,Sn取最大值49.
则Sn的图象如图所示
又S3=S11
所以图象的对称轴为
7
n
11
3
Sn
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法3
由S3=S11得
d=-2
∴当n=7时,Sn取最大值49.
∴ an=13+(n-1) ×(-2)=-2n+15
由
得
∴a7+a8=0
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法4
由S3=S11得
∴当n=7时,Sn取最大值49.
a4+a5+a6+……+a11=0
而 a4+a11=a5+a10=a6+a9=a7+a8
又d=-2<0,a1=13>0
∴a7>0,a8<0
等差数列的前n项的最值问题
一、
例8.设等差数列的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围;
(2)指出数列{Sn}中数值最大的项,并说明理由.
解:(1)由已知得
a1+2d=12
12a1+6×11d>0
113a1+13×6d<0
a3=12,
S12>0,
S13<0.
(2) ∵
∴Sn图象的对称轴为
由(1)知
由上得
即
∴Sn有最大值.
Sn =a1 + a2 +…+an,
S2n-Sn=an+1 +an+2 +…+a2n,
S3n-S2n=a2n+1+a2n+2+…+a3n,
x
x
2x
3x
4x
(2)一个等差数列前n项和为25,前2n项和为100,求其前3n项的和.
解析:(1)由题意知
S4=30,S8-S4=80.
∵S4,S8-S4,S12-S8成等差数列,
∴30、80、S12-S8成等差数列.
∴S12-S8=130.
而S12-S8=a9+a10+a11+a12,
(2)Sn=25,S2n=100.设S3n=x.
由于Sn,S2n-Sn,S3n-S2n成等差数列,
∴25,100-25,x-100成等差数列.
∴(x-100)+25=2(100-25).
∴x-100+25=150.
∴x=225,
∴S3n=225.
S4
S8-S4
S12-S8
例2.在等差数列{an}中,S10=100,S100=10.求S110.
例2.在等差数列{an}中,S10=100,S100=10.求S110.
解得d=-22.
若项数为2n,则
S偶-S奇=a2+a4+a6+…+a2n-a1-a3-a5-…-a2n-1
=d+d+…+d
=nd,
S12=354
S偶∶S奇=32∶27
等差数列{an}前n项和的性质
性质2:Sn,S2n-Sn,S3n-S2n, …也是等差数列, 公差为
在等差数列{an}中,其前n项的和为Sn,则有
n2d
性质1: 为等差数列.
性质3:若数列{an}与{bn}都是等差数列,且前n项的和分别为Sn和Tn,则
(2)若项数为奇数2n-1,则
S2n-1=(2n- 1)an (an为中间项),
此时有:S奇-S偶= ,
an
性质5:若Sm=p,Sp=m(m≠p),则Sm+p=
- (m+p)
性质6:若Sm=Sp (m≠p),则 Sp+m=
0
性质4:(1)若项数为偶数2n,则
S2n=n(a1+a2n)=n(an+an+1) (an,an+1为中间项),
此时有:S偶-S奇= ,
nd
等差数列的前n项和
的性质及应用
等差数列的前n项和公式:
形式1:
形式2:
复习回顾
S n与
之间的关系:
当n = 1时,
当n ≥ 2时,
1.将等差数列前n项和公式
看作是一个关于n的函数,这个函数有什么特点?
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
令
A
B
等差数列的前n项的最值问题
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法1
由S3=S11得
∴ d=-2
∴当n=7时,Sn取最大值49.
7
n
11
3
Sn
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法2
由S3=S11得
d=-2<0
∴当n=7时,Sn取最大值49.
则Sn的图象如图所示
又S3=S11
所以图象的对称轴为
7
n
11
3
Sn
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法3
由S3=S11得
d=-2
∴当n=7时,Sn取最大值49.
∴ an=13+(n-1) ×(-2)=-2n+15
由
得
∴a7+a8=0
例1.已知等差数列{an}中,a1=13且S3=S11,求n取何值时,Sn取最大值.
解法4
由S3=S11得
∴当n=7时,Sn取最大值49.
a4+a5+a6+……+a11=0
而 a4+a11=a5+a10=a6+a9=a7+a8
又d=-2<0,a1=13>0
∴a7>0,a8<0
等差数列的前n项的最值问题
一、
例8.设等差数列的前n项和为Sn,已知a3=12,S12>0,S13<0.
(1)求公差d的取值范围;
(2)指出数列{Sn}中数值最大的项,并说明理由.
解:(1)由已知得
a1+2d=12
12a1+6×11d>0
113a1+13×6d<0
a3=12,
S12>0,
S13<0.
(2) ∵
∴Sn图象的对称轴为
由(1)知
由上得
即
∴Sn有最大值.
Sn =a1 + a2 +…+an,
S2n-Sn=an+1 +an+2 +…+a2n,
S3n-S2n=a2n+1+a2n+2+…+a3n,
x
x
2x
3x
4x
(2)一个等差数列前n项和为25,前2n项和为100,求其前3n项的和.
解析:(1)由题意知
S4=30,S8-S4=80.
∵S4,S8-S4,S12-S8成等差数列,
∴30、80、S12-S8成等差数列.
∴S12-S8=130.
而S12-S8=a9+a10+a11+a12,
(2)Sn=25,S2n=100.设S3n=x.
由于Sn,S2n-Sn,S3n-S2n成等差数列,
∴25,100-25,x-100成等差数列.
∴(x-100)+25=2(100-25).
∴x-100+25=150.
∴x=225,
∴S3n=225.
S4
S8-S4
S12-S8
例2.在等差数列{an}中,S10=100,S100=10.求S110.
例2.在等差数列{an}中,S10=100,S100=10.求S110.
解得d=-22.
若项数为2n,则
S偶-S奇=a2+a4+a6+…+a2n-a1-a3-a5-…-a2n-1
=d+d+…+d
=nd,
S12=354
S偶∶S奇=32∶27
等差数列{an}前n项和的性质
性质2:Sn,S2n-Sn,S3n-S2n, …也是等差数列, 公差为
在等差数列{an}中,其前n项的和为Sn,则有
n2d
性质1: 为等差数列.
性质3:若数列{an}与{bn}都是等差数列,且前n项的和分别为Sn和Tn,则
(2)若项数为奇数2n-1,则
S2n-1=(2n- 1)an (an为中间项),
此时有:S奇-S偶= ,
an
性质5:若Sm=p,Sp=m(m≠p),则Sm+p=
- (m+p)
性质6:若Sm=Sp (m≠p),则 Sp+m=
0
性质4:(1)若项数为偶数2n,则
S2n=n(a1+a2n)=n(an+an+1) (an,an+1为中间项),
此时有:S偶-S奇= ,
nd
