北师大版七年级上册5.6 应用一元一次方程-追赶小明(课件)(共21张PPT)
文档属性
| 名称 | 北师大版七年级上册5.6 应用一元一次方程-追赶小明(课件)(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
第五章 一元一次方程
6.应用一元一次方程
—追赶小明
北师大版七年级数学上册
学习&目标
1.学会利用线段图分析行程问题,寻找等量关系,建立数学模型.(难点)
2.能利用行程中的速度、路程、时间之间的关系列方程解应用题.(重点)
情境&导入
你知道它蕴含的是我们数学中的什么问题吗?
情境&导入
探索&交流
一般行程问题
知识点一
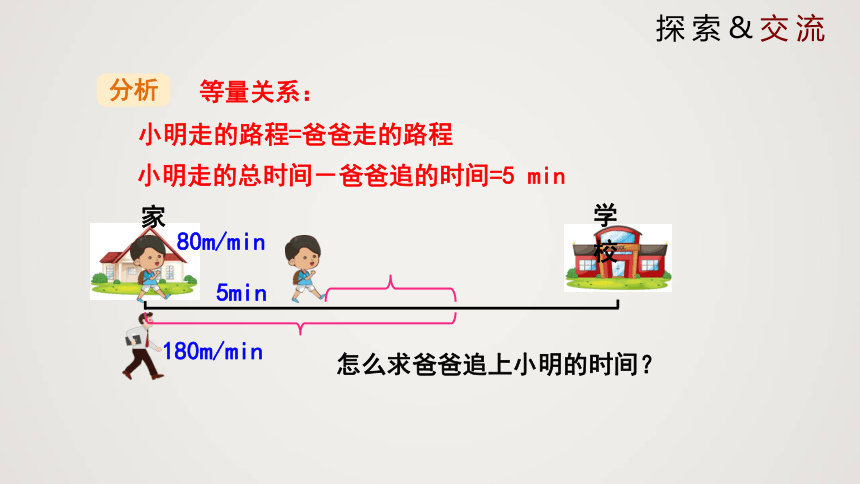
小明每天早上要在7: 50之前赶到距家1 000 m的学校上学.一天,小明以80 m/min的速度出发,5 min后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180 m/min的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
探索&交流
分析
家
学校
80m/min
小明走的路程=爸爸走的路程
等量关系:
5min
180m/min
怎么求爸爸追上小明的时间?
小明走的总时间-爸爸追的时间=5 min
探索&交流
1.用简单的“线段图”表示演示的追赶过程.
80×5
80x
180x
2.路程、速度和时间三者之间有何关系呢?“线段图”反映了怎样的等量关系?
家
学校
探索&交流
解得 x=4
(1)设爸爸追上小明用了x min
80×5+80x=180x
因此,爸爸追上小明用了4min。
解:
小明:
爸爸:
80×5
80x
180x
根据题意得:
探索&交流
(2)追上小明时,距离学校还有多远?
180×4
1000 m
?
解:
180×4=720(m)
1000-720=280(m)
所以,追上小明时,距离学校还有280 m。
总结:1.行程问题的基本关系式:
路程=速度×时间;
时间=路程÷速度,速度=路程÷时间.
2.行程问题中的等量关系:
(1)相遇问题中的等量关系:
①甲走的路程+乙走的路程=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
探索&交流
(2)追及问题中的等量关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间
例题&解析
例题欣赏
例1.A,B两地相距60千米,甲、乙两人分别从A,B两地出发相向而行,甲的速度是8千米/时,乙的速度是6千米/时.经过多长时间两人相距4千米?
8x
6x
60
4
A
B
8x
6x
60
4
A
B
探索&交流
两人从两地出发相向而行的行程问题称为相遇问题.
往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.
总结
例题&解析
例题欣赏
例2.一艘轮船在A、B两地之间航行,顺流用3h,逆流航行比顺流航行多用30min,轮船在静水中的速度为26km/h,求水流的速度。
顺水中的航速=静水中的航速 +水流速度
顺水中
逆水中
3h
等量关系:
3.5h
逆水中的航速=静水中的航速-水流速度
26km/h
顺水中的航程=逆水中的航程
分析
设水流速度为x千米/小时
解:
3(x+26)=3.5(26-x)
解得:x=2
答:水流速度为2千米/小时
例题&解析
例题&解析
例题欣赏
例3.小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步.小明跑2圈用的时间和他的哥哥跑3圈用的时间相等.两人同时同地同向出发,结果经过2 min 40 s他们第一次相遇,若他们两人同时同地反向出发,则经过几秒他们第一次相遇?
例题&解析
解:设小明的速度为x m/s,
则他的哥哥的速度为 x m/s,
由题意得160x=160× -400.
解得x=5.
则小明的哥哥的速度为5× =7.5(m/s).
设经过y s他们第一次相遇,
由题意,得(5+7.5)y=400.解得y=32.
答:经过32s他们第一次相遇.
环形跑道问题:设v甲>v乙,环形跑道长s米,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
总结
①同时同地、同向而行:
v甲t-v乙t=s.
①同时同地、背向而行:
v甲t+v乙t=s.
探索&交流
练习&巩固
1.某船顺流航行的速度为20 km/h,逆流航行的速度为16 km/h,则水流速度为(单位:km/h)( ).
A.2 B.4 C.18 D.36
练习&巩固
2.张昆早晨去学校共用时15 min,他跑了一段,走了一段,他跑步的平均速度是250 m/min,步行的平均速度是80 m/min,他家与学校的距离是2 900 m,若他跑步的时间为x min,则列出的方程是( )
A.250x+80 =2 900
B.80x+250(15-x)=2 900
C.80x+250 =2 900
D.250x+80(15-x)=2 900
练习&巩固
3.一架战斗机的贮油量最多够它在空中飞行4.6 h,飞机出航时顺风飞行,在无风时的速度是575 km/h,风速为25 km/h,这架飞机最远能飞出多少千米就应返回?
小结&反思
行程问题有相遇问题,追及问题,顺流、逆流问题,上坡、下坡问题等.在运动形式上分直线运动及曲线运动(如环形跑道).相遇问题是相向而行,相遇时的总路程为两运动物体的路程和.追及问题是同向而行,分慢的在快的前面或慢的先行若干时间,快的再追.顺流、逆流、顺风、逆风、上下坡问题应注意运动方向.
第五章 一元一次方程
6.应用一元一次方程
—追赶小明
北师大版七年级数学上册
学习&目标
1.学会利用线段图分析行程问题,寻找等量关系,建立数学模型.(难点)
2.能利用行程中的速度、路程、时间之间的关系列方程解应用题.(重点)
情境&导入
你知道它蕴含的是我们数学中的什么问题吗?
情境&导入
探索&交流
一般行程问题
知识点一
小明每天早上要在7: 50之前赶到距家1 000 m的学校上学.一天,小明以80 m/min的速度出发,5 min后,小明的爸爸发现他忘了带语文书.于是,爸爸立即以180 m/min的速度去追小明,并且在途中追上了他.
(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?
探索&交流
分析
家
学校
80m/min
小明走的路程=爸爸走的路程
等量关系:
5min
180m/min
怎么求爸爸追上小明的时间?
小明走的总时间-爸爸追的时间=5 min
探索&交流
1.用简单的“线段图”表示演示的追赶过程.
80×5
80x
180x
2.路程、速度和时间三者之间有何关系呢?“线段图”反映了怎样的等量关系?
家
学校
探索&交流
解得 x=4
(1)设爸爸追上小明用了x min
80×5+80x=180x
因此,爸爸追上小明用了4min。
解:
小明:
爸爸:
80×5
80x
180x
根据题意得:
探索&交流
(2)追上小明时,距离学校还有多远?
180×4
1000 m
?
解:
180×4=720(m)
1000-720=280(m)
所以,追上小明时,距离学校还有280 m。
总结:1.行程问题的基本关系式:
路程=速度×时间;
时间=路程÷速度,速度=路程÷时间.
2.行程问题中的等量关系:
(1)相遇问题中的等量关系:
①甲走的路程+乙走的路程=甲、乙出发点之间的路程;
②若甲、乙同时出发,甲用的时间=乙用的时间.
探索&交流
(2)追及问题中的等量关系:
①快者走的路程-慢者走的路程=追及路程;
②若同时出发,快者追上慢者时,快者用的时间=慢者用的时间
例题&解析
例题欣赏
例1.A,B两地相距60千米,甲、乙两人分别从A,B两地出发相向而行,甲的速度是8千米/时,乙的速度是6千米/时.经过多长时间两人相距4千米?
8x
6x
60
4
A
B
8x
6x
60
4
A
B
探索&交流
两人从两地出发相向而行的行程问题称为相遇问题.
往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.
总结
例题&解析
例题欣赏
例2.一艘轮船在A、B两地之间航行,顺流用3h,逆流航行比顺流航行多用30min,轮船在静水中的速度为26km/h,求水流的速度。
顺水中的航速=静水中的航速 +水流速度
顺水中
逆水中
3h
等量关系:
3.5h
逆水中的航速=静水中的航速-水流速度
26km/h
顺水中的航程=逆水中的航程
分析
设水流速度为x千米/小时
解:
3(x+26)=3.5(26-x)
解得:x=2
答:水流速度为2千米/小时
例题&解析
例题&解析
例题欣赏
例3.小明和他的哥哥早晨起来沿长为400 m的环形跑道练习跑步.小明跑2圈用的时间和他的哥哥跑3圈用的时间相等.两人同时同地同向出发,结果经过2 min 40 s他们第一次相遇,若他们两人同时同地反向出发,则经过几秒他们第一次相遇?
例题&解析
解:设小明的速度为x m/s,
则他的哥哥的速度为 x m/s,
由题意得160x=160× -400.
解得x=5.
则小明的哥哥的速度为5× =7.5(m/s).
设经过y s他们第一次相遇,
由题意,得(5+7.5)y=400.解得y=32.
答:经过32s他们第一次相遇.
环形跑道问题:设v甲>v乙,环形跑道长s米,经过t秒甲、乙第一次相遇.
一般有如下两种情形:
总结
①同时同地、同向而行:
v甲t-v乙t=s.
①同时同地、背向而行:
v甲t+v乙t=s.
探索&交流
练习&巩固
1.某船顺流航行的速度为20 km/h,逆流航行的速度为16 km/h,则水流速度为(单位:km/h)( ).
A.2 B.4 C.18 D.36
练习&巩固
2.张昆早晨去学校共用时15 min,他跑了一段,走了一段,他跑步的平均速度是250 m/min,步行的平均速度是80 m/min,他家与学校的距离是2 900 m,若他跑步的时间为x min,则列出的方程是( )
A.250x+80 =2 900
B.80x+250(15-x)=2 900
C.80x+250 =2 900
D.250x+80(15-x)=2 900
练习&巩固
3.一架战斗机的贮油量最多够它在空中飞行4.6 h,飞机出航时顺风飞行,在无风时的速度是575 km/h,风速为25 km/h,这架飞机最远能飞出多少千米就应返回?
小结&反思
行程问题有相遇问题,追及问题,顺流、逆流问题,上坡、下坡问题等.在运动形式上分直线运动及曲线运动(如环形跑道).相遇问题是相向而行,相遇时的总路程为两运动物体的路程和.追及问题是同向而行,分慢的在快的前面或慢的先行若干时间,快的再追.顺流、逆流、顺风、逆风、上下坡问题应注意运动方向.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
