北师大版八年级上册1.3勾股定理的应用课件(共25张PPT)
文档属性
| 名称 | 北师大版八年级上册1.3勾股定理的应用课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 08:42:13 | ||
图片预览






文档简介
(共25张PPT)
1.3勾股定理的应用
数学(北师大版)
八年级 上册
第一章
勾股定理
学习目标
1.应用“勾股定理”解决实际问题。体会把立体图形转化为平面图形,解决“最短路径”的问题。树立转化思想。
2.会根据“勾股定理的逆定理”解决实际问题。
3.利用数学中的“建模思想”构造直角三角形,利用勾股定理及逆定理,解决实际问题。
导入新课
如果直角三角形两直角边分别为a,b斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。且边C所对的角为直角.最长的边为斜边。
a2 + b2 = c2
勾股定理的逆定理
导入新课
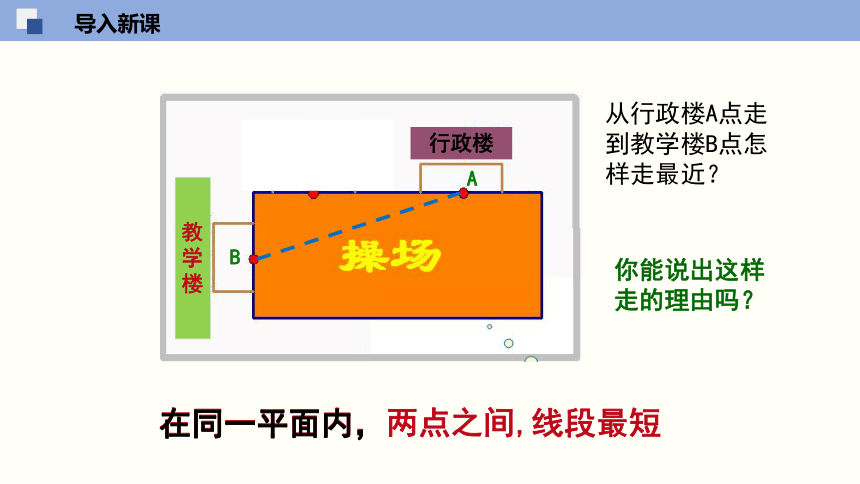
在同一平面内,两点之间,线段最短
从行政楼A点走到教学楼B点怎样走最近?
教学楼
行政楼
B
A
你能说出这样走的理由吗?
在同一平面内,
讲授新课
立体图形中两点之间的最短距离
一
B
A
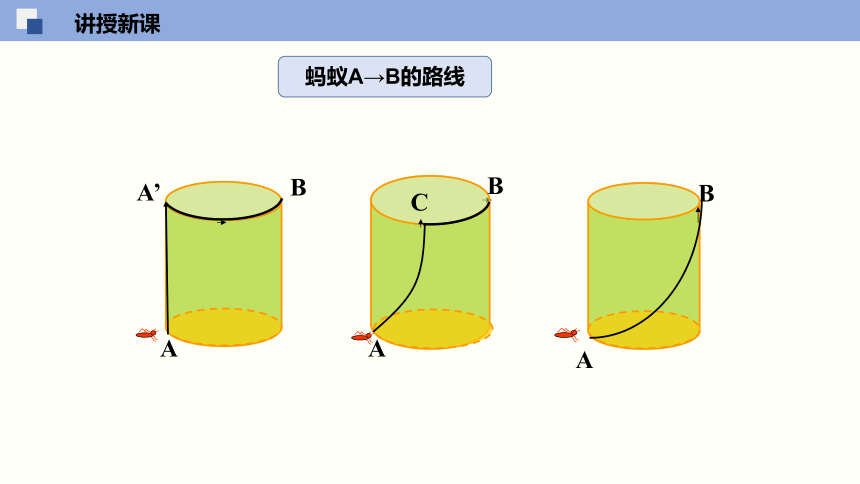
小明喝完饮料,在无盖圆柱形饮料杯口B处有剩余,甜甜的气味恰好被一只在点A处的蚂蚁捕捉到,于是它想从点A处爬到点B处,想一想,沿圆柱侧面你能为蚂蚁设计怎样的路线?
讲授新课
A
B
A’
A
B
B
A
蚂蚁A→B的路线
C
讲授新课
A
A
C
B
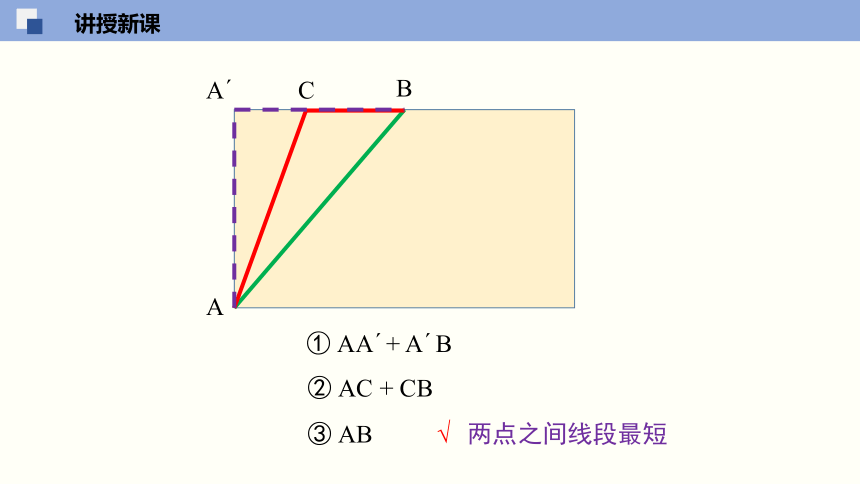
① AA + A B
② AC + CB
③ AB
√ 两点之间线段最短
讲授新课
若已知圆柱体高为12 cm,底面半径为3 cm,
π取3,则:
B
A
3
O
12
侧面展开图
12
3π
A
B
【方法归纳】立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
A'
A'
讲授新课
立体图形 平面图形 直角三角形
思维导图:
转化
建模
两点之间线段最短
勾股定理
分类讨论
讲授新课
B
牛奶盒
A
变式2:看到小蚂蚁终于喝到饮料的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程么?
6cm
8cm
10cm
讲授新课
B
B1
8
A
B2
6
10
B3
AB12 =102 +(6+8)2 =296
AB22= 82 +(10+6)2 =320
AB32= 62 +(10+8)2 =360
讲授新课
例:如把正方体变成如左图的长方体,长方体底面长为2,宽为1,高为4,蚂蚁从A点沿长方体表面爬到E点有多少种爬行可能?那种爬行路径的距离最短?是多少?
讲授新课
解:长方体侧面展开图一共有三种情况,如上图,其距离分别是:
第一种:
第二种:
第三种:
D
A
G
H
F
E
2
4
1
左(右)
上(下)
(1)
B
A
G
F
H
E
2
4
1
前(后)
上(下)
(2)
A
B
C
F
G
E
4
1
2
前
(后)
右(左)
(3)
总结:四棱柱给出的长、宽、高三个数据,把较小的两个数据的和作为一条直角边的长,最大的数据作为另一条直角边的长,这时斜边的长即为最短距离。
讲授新课
问题:李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
解:连接对角线AC,只要分别量出AB、BC、AC的长度即可.
AB2+BC2=AC2
△ABC为直角三角形
勾股定理的实际应用
二
讲授新课
(2)量得AD长是30 cm,AB长是40 cm,BD长是50 cm. AD边垂直于AB边吗?
解:AD2+AB2=302+402=502=BD2,
得∠DAB=90°,AD边垂直于AB边.
讲授新课
(3)若随身只有一个长度为20 cm的刻度尺,能有办法检验AD边是否垂直于AB边吗?
解:在AD上取点M,使AM=9,在AB上取点N使AN=12,测量MN是否是15,是,就是垂直;不是,就是不垂直.
当堂检测
1.如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm C.6 cm D.10 cm
B
当堂检测
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为x米,即AB=x米,而AC=2米,BC=1.5米,有
故,最长是2.5+0.5=3(米)
答:这根铁棒的最长3米,最短2米.
故,最短是1.5+0.5=2(米)
当最短时:
A
C
B
最短是多少米?
当堂检测
3.如图,在棱长为10 cm的正方体的一个顶点A处有一
只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是
1 cm/s,且速度保持不变,问蚂蚁能否在20 s内从A爬
到B?
B
A
当堂检测
B
A
B
【解析】因为从A到B最短路径AB满足AB2=202+102=500>400,所以不能在20 s内从A爬到B.
当堂检测
解析:∵AB=6.5米,BC=2.5米,∠C=90°,
∴AC2=AB2-BC2=62,
∴AC=6米,
∴地毯的长度为AC+BC=6+2.5=8.5(米),
∴地毯的面积为8.5×6=51(平方米).
故填51平方米.
4.某楼梯的侧面视图如图所示,其中AB=6.5米,BC=2.5米,∠C=90°,楼梯的宽度为6米,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的面积应为 .
51平方米
当堂检测
5. 如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长.
故滑道AC的长度为5 m.
解:设滑道AC的长度为x m,则AB的长也为x m,AE的长度为(x-1)m.
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE2+CE2=AC2,
即(x-1)2+32=x2,
解得x=5.
当堂检测
6、 有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少
5尺
1尺
x 尺
水池
解:设这个水池的深度为 尺
∴深度为12尺,芦苇长度为13尺
课堂小结
注意:运用勾股定理解决实际问题时,
①、没有图的要按题意画好图并标上字母;
②、有时必须设好未知数,并根据勾股定理列出相应的方程式才能做出答案。
数学问题
转化
实际问题
谢谢~
1.3勾股定理的应用
数学(北师大版)
八年级 上册
第一章
勾股定理
学习目标
1.应用“勾股定理”解决实际问题。体会把立体图形转化为平面图形,解决“最短路径”的问题。树立转化思想。
2.会根据“勾股定理的逆定理”解决实际问题。
3.利用数学中的“建模思想”构造直角三角形,利用勾股定理及逆定理,解决实际问题。
导入新课
如果直角三角形两直角边分别为a,b斜边为c,那么
a2 + b2 = c2
勾股定理
如果三角形的三边长a、b、c满足 ,那么这个三角形是直角三角形。且边C所对的角为直角.最长的边为斜边。
a2 + b2 = c2
勾股定理的逆定理
导入新课
在同一平面内,两点之间,线段最短
从行政楼A点走到教学楼B点怎样走最近?
教学楼
行政楼
B
A
你能说出这样走的理由吗?
在同一平面内,
讲授新课
立体图形中两点之间的最短距离
一
B
A
小明喝完饮料,在无盖圆柱形饮料杯口B处有剩余,甜甜的气味恰好被一只在点A处的蚂蚁捕捉到,于是它想从点A处爬到点B处,想一想,沿圆柱侧面你能为蚂蚁设计怎样的路线?
讲授新课
A
B
A’
A
B
B
A
蚂蚁A→B的路线
C
讲授新课
A
A
C
B
① AA + A B
② AC + CB
③ AB
√ 两点之间线段最短
讲授新课
若已知圆柱体高为12 cm,底面半径为3 cm,
π取3,则:
B
A
3
O
12
侧面展开图
12
3π
A
B
【方法归纳】立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
A'
A'
讲授新课
立体图形 平面图形 直角三角形
思维导图:
转化
建模
两点之间线段最短
勾股定理
分类讨论
讲授新课
B
牛奶盒
A
变式2:看到小蚂蚁终于喝到饮料的兴奋劲儿,小明又灵光乍现,拿出了牛奶盒,把小蚂蚁放在了点A处,并在点B处放上了点儿火腿肠粒,你能帮小蚂蚁找到完成任务的最短路程么?
6cm
8cm
10cm
讲授新课
B
B1
8
A
B2
6
10
B3
AB12 =102 +(6+8)2 =296
AB22= 82 +(10+6)2 =320
AB32= 62 +(10+8)2 =360
讲授新课
例:如把正方体变成如左图的长方体,长方体底面长为2,宽为1,高为4,蚂蚁从A点沿长方体表面爬到E点有多少种爬行可能?那种爬行路径的距离最短?是多少?
讲授新课
解:长方体侧面展开图一共有三种情况,如上图,其距离分别是:
第一种:
第二种:
第三种:
D
A
G
H
F
E
2
4
1
左(右)
上(下)
(1)
B
A
G
F
H
E
2
4
1
前(后)
上(下)
(2)
A
B
C
F
G
E
4
1
2
前
(后)
右(左)
(3)
总结:四棱柱给出的长、宽、高三个数据,把较小的两个数据的和作为一条直角边的长,最大的数据作为另一条直角边的长,这时斜边的长即为最短距离。
讲授新课
问题:李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB,但他随身只带了卷尺.
(1)你能替他想办法完成任务吗?
解:连接对角线AC,只要分别量出AB、BC、AC的长度即可.
AB2+BC2=AC2
△ABC为直角三角形
勾股定理的实际应用
二
讲授新课
(2)量得AD长是30 cm,AB长是40 cm,BD长是50 cm. AD边垂直于AB边吗?
解:AD2+AB2=302+402=502=BD2,
得∠DAB=90°,AD边垂直于AB边.
讲授新课
(3)若随身只有一个长度为20 cm的刻度尺,能有办法检验AD边是否垂直于AB边吗?
解:在AD上取点M,使AM=9,在AB上取点N使AN=12,测量MN是否是15,是,就是垂直;不是,就是不垂直.
当堂检测
1.如图是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm C.6 cm D.10 cm
B
当堂检测
有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边壁的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒最长是多少米?
解:图形可简化为左下图,设伸入油桶中的长度为x米,即AB=x米,而AC=2米,BC=1.5米,有
故,最长是2.5+0.5=3(米)
答:这根铁棒的最长3米,最短2米.
故,最短是1.5+0.5=2(米)
当最短时:
A
C
B
最短是多少米?
当堂检测
3.如图,在棱长为10 cm的正方体的一个顶点A处有一
只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是
1 cm/s,且速度保持不变,问蚂蚁能否在20 s内从A爬
到B?
B
A
当堂检测
B
A
B
【解析】因为从A到B最短路径AB满足AB2=202+102=500>400,所以不能在20 s内从A爬到B.
当堂检测
解析:∵AB=6.5米,BC=2.5米,∠C=90°,
∴AC2=AB2-BC2=62,
∴AC=6米,
∴地毯的长度为AC+BC=6+2.5=8.5(米),
∴地毯的面积为8.5×6=51(平方米).
故填51平方米.
4.某楼梯的侧面视图如图所示,其中AB=6.5米,BC=2.5米,∠C=90°,楼梯的宽度为6米,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的面积应为 .
51平方米
当堂检测
5. 如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长.已知滑梯的高度CE=3m,CD=1m,试求滑道AC的长.
故滑道AC的长度为5 m.
解:设滑道AC的长度为x m,则AB的长也为x m,AE的长度为(x-1)m.
在Rt△ACE中,∠AEC=90°,
由勾股定理得AE2+CE2=AC2,
即(x-1)2+32=x2,
解得x=5.
当堂检测
6、 有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少
5尺
1尺
x 尺
水池
解:设这个水池的深度为 尺
∴深度为12尺,芦苇长度为13尺
课堂小结
注意:运用勾股定理解决实际问题时,
①、没有图的要按题意画好图并标上字母;
②、有时必须设好未知数,并根据勾股定理列出相应的方程式才能做出答案。
数学问题
转化
实际问题
谢谢~
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
