北师大版九年级下册3.2 圆的对称性课件(共41张PPT)
文档属性
| 名称 | 北师大版九年级下册3.2 圆的对称性课件(共41张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 00:00:00 | ||
图片预览





文档简介
(共41张PPT)
3.2 圆的对称性
北师大版九年级下册
导入新课
讲授新课
当堂练习
课堂小结
1.掌握圆是轴对称图形及圆的中心对称性和旋转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问题.(重点)
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.(难点)
学习目标
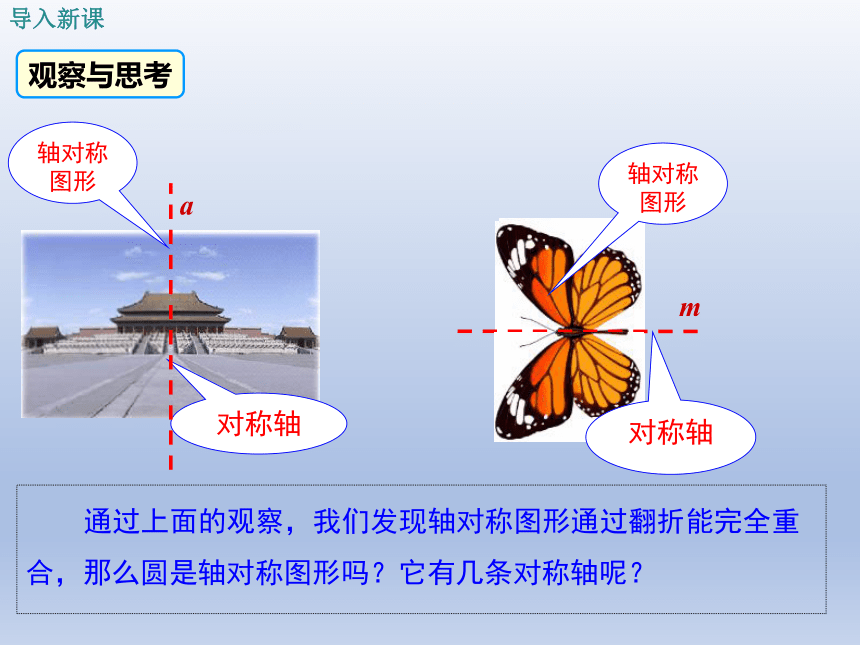
通过上面的观察,我们发现轴对称图形通过翻折能完全重合,那么圆是轴对称图形吗?它有几条对称轴呢?
轴对称图形
轴对称图形
对称轴
对称轴
a
m
导入新课
观察与思考
讲授新课
圆的对称性
一
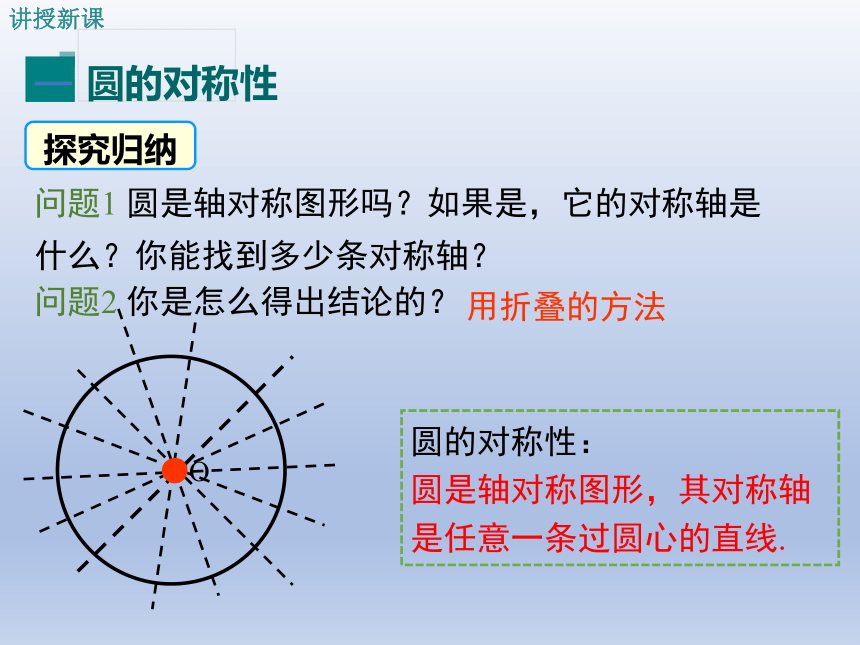
问题1 圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
问题2 你是怎么得出结论的?
圆的对称性: 圆是轴对称图形,其对称轴是任意一条过圆心的直线.
用折叠的方法
●O
探究归纳
.
O
A
B
180°
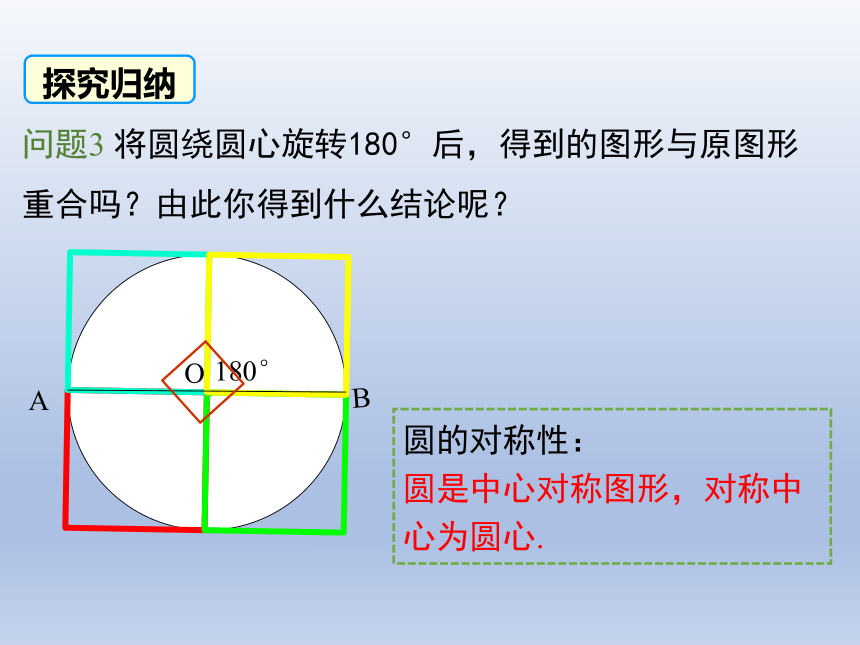
问题3 将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
探究归纳
圆的对称性: 圆是中心对称图形,对称中心为圆心.
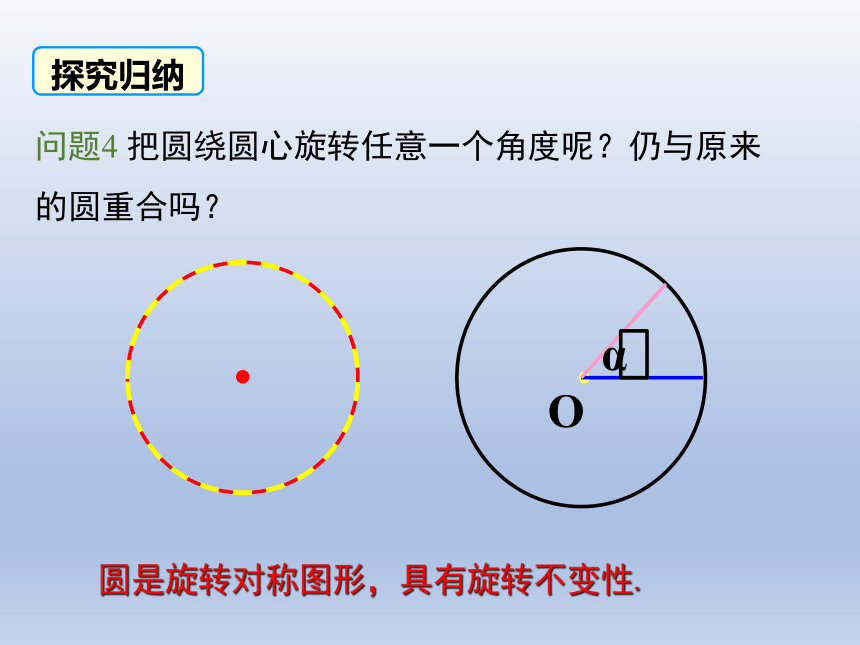
问题4 把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
圆是旋转对称图形,具有旋转不变性.
·
探究归纳
圆的中心对称性
一个圆绕着它的圆心旋转任意一个角度,
还能与原来的图形重合吗?
结论1:一个圆绕着它的圆心旋转任意一个角
度,都能与原来的图形重合,我们把
圆的这个特性称之为圆的旋转不变性.
结论2:圆是中心对称图形,对称中心为圆心.
观察:
结论:我们可以通过折叠的方法得到圆是轴
对称图形,经过圆心的一条直线是圆
的对称轴,圆的对称轴有无数条.
圆的对称性
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
注意:
对称轴是直线,不能说每一条直径都是它的对称轴;
1.利用一个圆及其若干条弦分别设
计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)是中心对称图形但不是轴对称图形;
(3)既是轴对称图形又是中心对称图形.
第(1)问图
第(2)问图
第(3)问图
2.下述命题是否正确?为什么?
圆只有一条对称轴.
有无数条对称轴任意一条直径所在的直线都是它的对称轴.
错
做一做:
1.圆:平面上到____________等于______
的所有点组成的图形叫做圆,其中______为
圆心,定长为________.
2.弧:圆上_________________叫做圆弧,简称
弧,圆的任意一条____的两个端点分圆成两条
弧,每一条弧都叫做圆的半径.
___________称为优弧,___________称为劣弧.
3._______________叫做等圆,
_____________________________叫做等弧.
定点的距离
定长
定点
半径
任意两点之间的部分
弦
大于半圆的弧
小于半圆的弧
能够重合的两个圆
在同圆或等圆中,能够重合的两条弧
在同圆中探究
在⊙O中,如果∠AOB= ∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
圆心角、弧、弦之间的关系
二
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么, ,弦AB=弦CD
归纳
O ′
·
O
A
B
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
·
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
归纳
⌒
⌒
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
要点归纳
弧、弦与圆心角的关系定理
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
在同圆或等圆中
题设
结论
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
要点归纳
×
×
√
抢答题
1.等弦所对的弧相等. ( )
2.等弧所对的弦相等. ( )
3.圆心角相等,所对的弦相等. ( )
关系定理及推论的运用
三
典例精析
例1 如图,AB,DE是⊙O 的直径,C是⊙O 上的一点,
且AD=CE.BE和CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE.理由是:
∵∠AOD=∠BOE,
∴AD=BE.
又∵AD=CE,
∴BE=CE.
∴BE=CE.
⌒ ⌒
⌒ ⌒
⌒ ⌒
⌒ ⌒
解:
∵
例2 如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
证明:
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
例3 如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒ ⌒
温馨提示:本题告诉我们,弧、圆心角、弦灵活转化是解题的关键.
∵AB=CD,
⌒ ⌒
填一填: 如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么_________,____________.
(2)如果 ,那么_________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
E
F
O
AB=CD
AB=CD
AB=CD
(
(
∠AOB= ∠COD
∠AOB= ∠COD
AB=CD
(
(
AB=CD
(
(
针对训练
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
解:OE=OF.
理由如下:
·
C
A
B
D
E
F
O
1 已知⊙O的半径为4cm,如果点P到圆心O的距离为4.5cm,那么点P与⊙O有怎样的位置关系?如果点P到圆心O的距离为4cm、3cm呢?
如何判断点与圆的位置关系?
只需要比较点到圆心的距离d与半径r的大小关系.
解:
设⊙O的半径为rcm,点P到圆心O的距离为dcm.
由题意得,r=4cm.
当d=4.5cm时, ∵ d>r,∴点P在⊙O外.
当d=4cm时, ∵ d=r,∴点P在⊙O上.
当d=3cm时, ∵ d<r,∴点P在⊙O内.
知识运用
如图,已知点A,请作出到点A的距离等于2cm的点的集合.
(1)这个圆的外部是满足什么条件的点的集合?
(2)请用阴影表示出到点A的距离小于或等于2cm的点的集合.
A
知识运用
已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点 B、C、D、E在以点M为圆心的同一圆上.
解题的依据:
要说明几点在同一个圆上,即说明这几个点到定点(圆心)的距离等于定长(半径).
到定点的距离等于定长的点在同一个圆上.
巩固练习
∴点B、C、D、E在以点M为圆心,
为半径的圆上.
解:
连接MD、ME.
∵BD、CE是△ABC的高,
∴∠BEC=∠BDC=90°.
在Rt△BEC中,M为BC的中点,
同理,
∴MB=ME=MD=MC,
又∵
已知:如图,BD、CE是△ABC的高,M为BC的中点.
试说明点 B、C、D、E在以点M为圆心的同一圆上.
练习:
E
E
例3:
在⊙O中, AC=BD,则AB与CD相等吗?为什么?
1.利用一个圆及若干条弦分别设计出符合下列条件的图案:
(3)即是轴对称图形又是中心对称图形.
(2)是中心对称图形但不是轴对称图形;
(1)是轴对称图形但不是中心对称图形;
∴∠AOC=∠BOC=60°,
2.已知A,B是⊙O上的两点,∠AOB=120 ° ,C是AB的中点,试确定四边形OACB的形状.
B
A
O
C
解:四边形OACB是菱形.
理由是:连接OC,
则有OA=OB=OC.
∵C是AB的中点,
∴AC=BC.
又∵∠AOB=120°,
∴△AOC与△BOC都是等边三角形.
∴OA=OB=AC=BC.
∴四边形OACB是菱形.
解:这两段弧的度数相等,但不能说这两段弧相等,因为这两个圆的半径不相等,所以90°的弧的弧长不相等.
任意画两个半径不相等的圆,然后在每一个圆上任意取一段90°的弧.这两段弧的度数相等吗?能说这两段弧相等吗?为什么?
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
在同圆或等圆中
应用提醒
①要注意前提条件;
②要灵活转化.
课堂小结
圆
圆是轴对称图形,其对称轴是任意一条过圆心的直线;
圆是中心对称图形,对称中心为圆心.
3.2 圆的对称性
北师大版九年级下册
导入新课
讲授新课
当堂练习
课堂小结
1.掌握圆是轴对称图形及圆的中心对称性和旋转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问题.(重点)
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.(难点)
学习目标
通过上面的观察,我们发现轴对称图形通过翻折能完全重合,那么圆是轴对称图形吗?它有几条对称轴呢?
轴对称图形
轴对称图形
对称轴
对称轴
a
m
导入新课
观察与思考
讲授新课
圆的对称性
一
问题1 圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
问题2 你是怎么得出结论的?
圆的对称性: 圆是轴对称图形,其对称轴是任意一条过圆心的直线.
用折叠的方法
●O
探究归纳
.
O
A
B
180°
问题3 将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
探究归纳
圆的对称性: 圆是中心对称图形,对称中心为圆心.
问题4 把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
圆是旋转对称图形,具有旋转不变性.
·
探究归纳
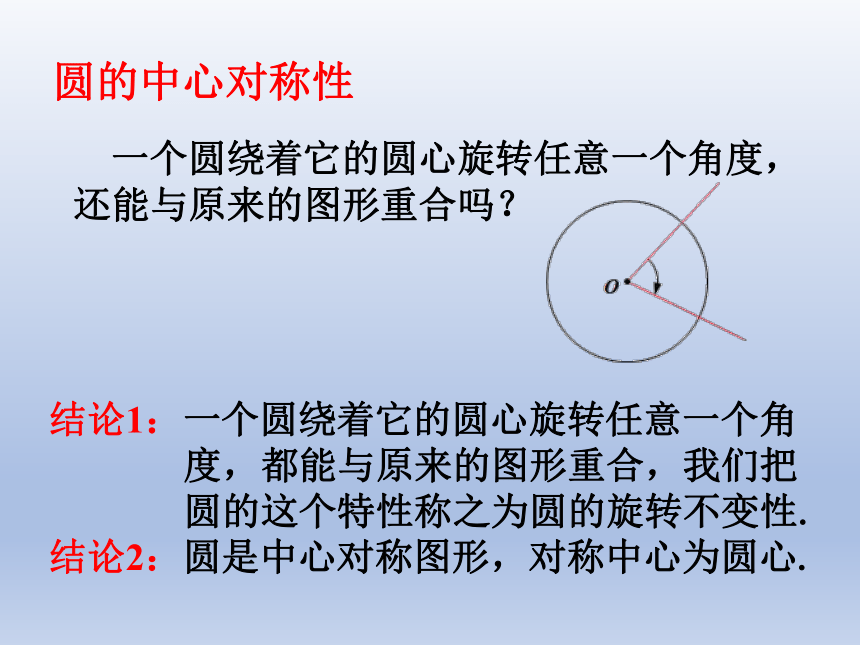
圆的中心对称性
一个圆绕着它的圆心旋转任意一个角度,
还能与原来的图形重合吗?
结论1:一个圆绕着它的圆心旋转任意一个角
度,都能与原来的图形重合,我们把
圆的这个特性称之为圆的旋转不变性.
结论2:圆是中心对称图形,对称中心为圆心.
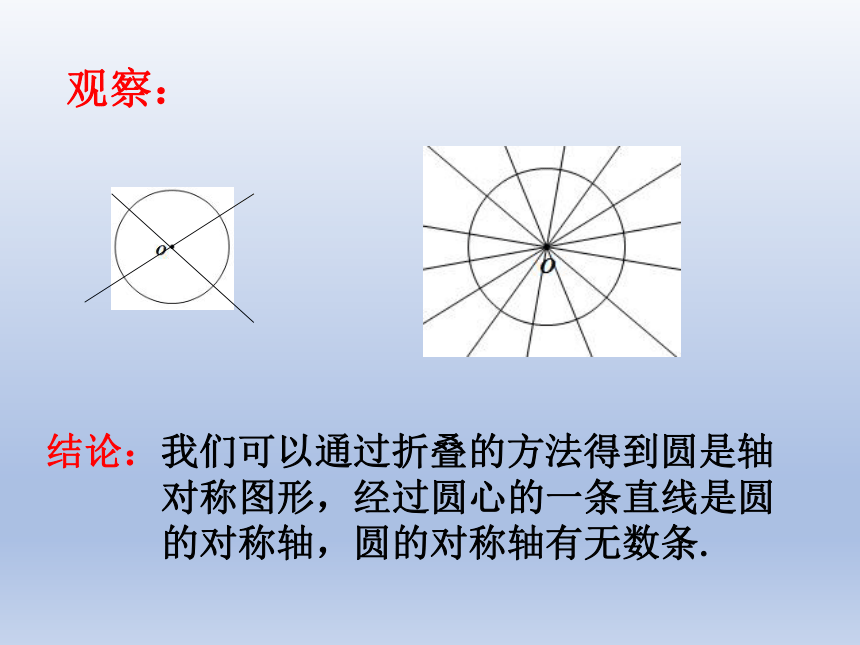
观察:
结论:我们可以通过折叠的方法得到圆是轴
对称图形,经过圆心的一条直线是圆
的对称轴,圆的对称轴有无数条.
圆的对称性
圆是轴对称图形.
圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.
●O
可利用折叠的方法即可解决上述问题.
注意:
对称轴是直线,不能说每一条直径都是它的对称轴;
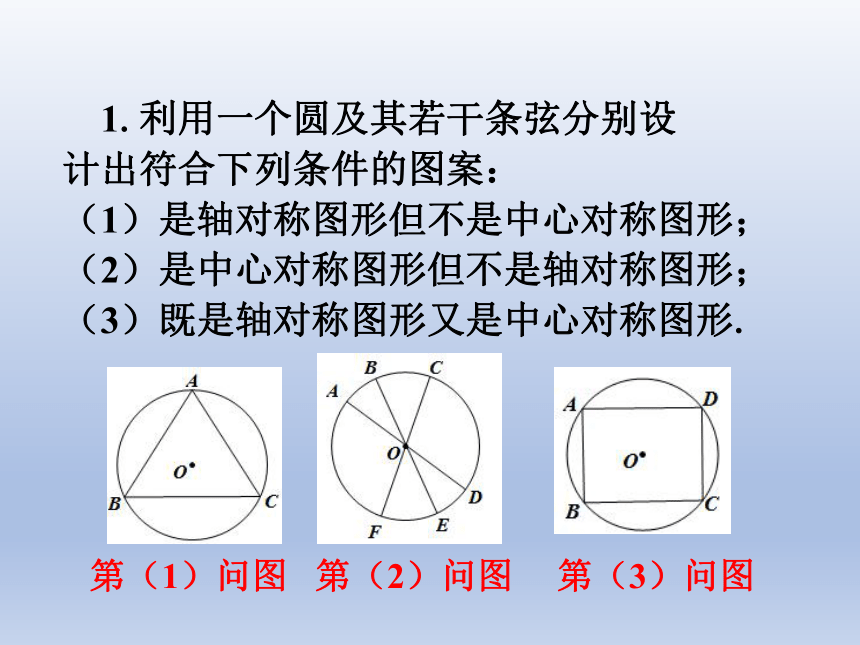
1.利用一个圆及其若干条弦分别设
计出符合下列条件的图案:
(1)是轴对称图形但不是中心对称图形;
(2)是中心对称图形但不是轴对称图形;
(3)既是轴对称图形又是中心对称图形.
第(1)问图
第(2)问图
第(3)问图
2.下述命题是否正确?为什么?
圆只有一条对称轴.
有无数条对称轴任意一条直径所在的直线都是它的对称轴.
错
做一做:
1.圆:平面上到____________等于______
的所有点组成的图形叫做圆,其中______为
圆心,定长为________.
2.弧:圆上_________________叫做圆弧,简称
弧,圆的任意一条____的两个端点分圆成两条
弧,每一条弧都叫做圆的半径.
___________称为优弧,___________称为劣弧.
3._______________叫做等圆,
_____________________________叫做等弧.
定点的距离
定长
定点
半径
任意两点之间的部分
弦
大于半圆的弧
小于半圆的弧
能够重合的两个圆
在同圆或等圆中,能够重合的两条弧
在同圆中探究
在⊙O中,如果∠AOB= ∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
圆心角、弧、弦之间的关系
二
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠COD,
那么, ,弦AB=弦CD
归纳
O ′
·
O
A
B
如图,在等圆中,如果∠AOB=∠CO ′ D,你发现的等量关系是否依然成立?为什么?
·
C
D
在等圆中探究
通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
归纳
⌒
⌒
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒ ⌒
③AB=CD
A
B
O
D
C
要点归纳
弧、弦与圆心角的关系定理
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
在同圆或等圆中
题设
结论
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
要点归纳
×
×
√
抢答题
1.等弦所对的弧相等. ( )
2.等弧所对的弦相等. ( )
3.圆心角相等,所对的弦相等. ( )
关系定理及推论的运用
三
典例精析
例1 如图,AB,DE是⊙O 的直径,C是⊙O 上的一点,
且AD=CE.BE和CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE.理由是:
∵∠AOD=∠BOE,
∴AD=BE.
又∵AD=CE,
∴BE=CE.
∴BE=CE.
⌒ ⌒
⌒ ⌒
⌒ ⌒
⌒ ⌒
解:
∵
例2 如图,AB是⊙O 的直径, ∠COD=35°,求∠AOE 的度数.
·
A
O
B
C
D
E
证明:
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
例3 如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒ ⌒
温馨提示:本题告诉我们,弧、圆心角、弦灵活转化是解题的关键.
∵AB=CD,
⌒ ⌒
填一填: 如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么_________,____________.
(2)如果 ,那么_________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
E
F
O
AB=CD
AB=CD
AB=CD
(
(
∠AOB= ∠COD
∠AOB= ∠COD
AB=CD
(
(
AB=CD
(
(
针对训练
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
解:OE=OF.
理由如下:
·
C
A
B
D
E
F
O
1 已知⊙O的半径为4cm,如果点P到圆心O的距离为4.5cm,那么点P与⊙O有怎样的位置关系?如果点P到圆心O的距离为4cm、3cm呢?
如何判断点与圆的位置关系?
只需要比较点到圆心的距离d与半径r的大小关系.
解:
设⊙O的半径为rcm,点P到圆心O的距离为dcm.
由题意得,r=4cm.
当d=4.5cm时, ∵ d>r,∴点P在⊙O外.
当d=4cm时, ∵ d=r,∴点P在⊙O上.
当d=3cm时, ∵ d<r,∴点P在⊙O内.
知识运用
如图,已知点A,请作出到点A的距离等于2cm的点的集合.
(1)这个圆的外部是满足什么条件的点的集合?
(2)请用阴影表示出到点A的距离小于或等于2cm的点的集合.
A
知识运用
已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点 B、C、D、E在以点M为圆心的同一圆上.
解题的依据:
要说明几点在同一个圆上,即说明这几个点到定点(圆心)的距离等于定长(半径).
到定点的距离等于定长的点在同一个圆上.
巩固练习
∴点B、C、D、E在以点M为圆心,
为半径的圆上.
解:
连接MD、ME.
∵BD、CE是△ABC的高,
∴∠BEC=∠BDC=90°.
在Rt△BEC中,M为BC的中点,
同理,
∴MB=ME=MD=MC,
又∵
已知:如图,BD、CE是△ABC的高,M为BC的中点.
试说明点 B、C、D、E在以点M为圆心的同一圆上.
练习:
E
E
例3:
在⊙O中, AC=BD,则AB与CD相等吗?为什么?
1.利用一个圆及若干条弦分别设计出符合下列条件的图案:
(3)即是轴对称图形又是中心对称图形.
(2)是中心对称图形但不是轴对称图形;
(1)是轴对称图形但不是中心对称图形;
∴∠AOC=∠BOC=60°,
2.已知A,B是⊙O上的两点,∠AOB=120 ° ,C是AB的中点,试确定四边形OACB的形状.
B
A
O
C
解:四边形OACB是菱形.
理由是:连接OC,
则有OA=OB=OC.
∵C是AB的中点,
∴AC=BC.
又∵∠AOB=120°,
∴△AOC与△BOC都是等边三角形.
∴OA=OB=AC=BC.
∴四边形OACB是菱形.
解:这两段弧的度数相等,但不能说这两段弧相等,因为这两个圆的半径不相等,所以90°的弧的弧长不相等.
任意画两个半径不相等的圆,然后在每一个圆上任意取一段90°的弧.这两段弧的度数相等吗?能说这两段弧相等吗?为什么?
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
在同圆或等圆中
应用提醒
①要注意前提条件;
②要灵活转化.
课堂小结
圆
圆是轴对称图形,其对称轴是任意一条过圆心的直线;
圆是中心对称图形,对称中心为圆心.
