15.4 角的平分线 (3) 教学课件(共25张PPT)
文档属性
| 名称 | 15.4 角的平分线 (3) 教学课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
沪科版 八年级上册
15.4角的平分线 (3)
掌握三角形三条内角平分线相交于一点,这点到三角形三边的距离相等这一性质.
教学重点:
教学难点:
教学目标:
会应用三角形的角平分线的性质解题.
应用三角形的角平分线的性质解题.
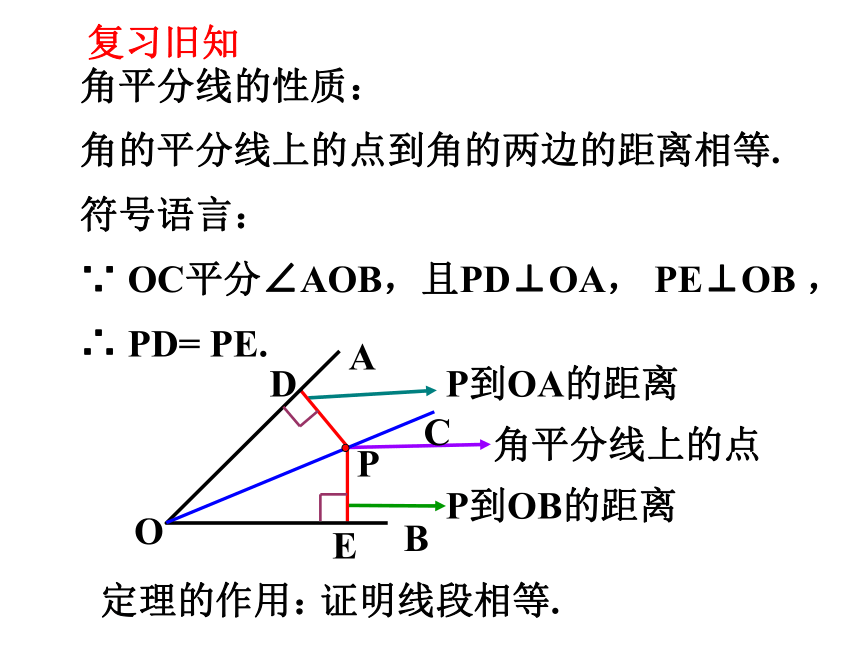
P到OA的距离
P到OB的距离
角平分线上的点
符号语言:
∵ OC平分∠AOB,且PD⊥OA, PE⊥OB ,
∴ PD= PE.
角的平分线上的点到角的两边的距离相等.
角平分线的性质:
O
D
E
P
A
C
B
定理的作用:
证明线段相等.
复习旧知
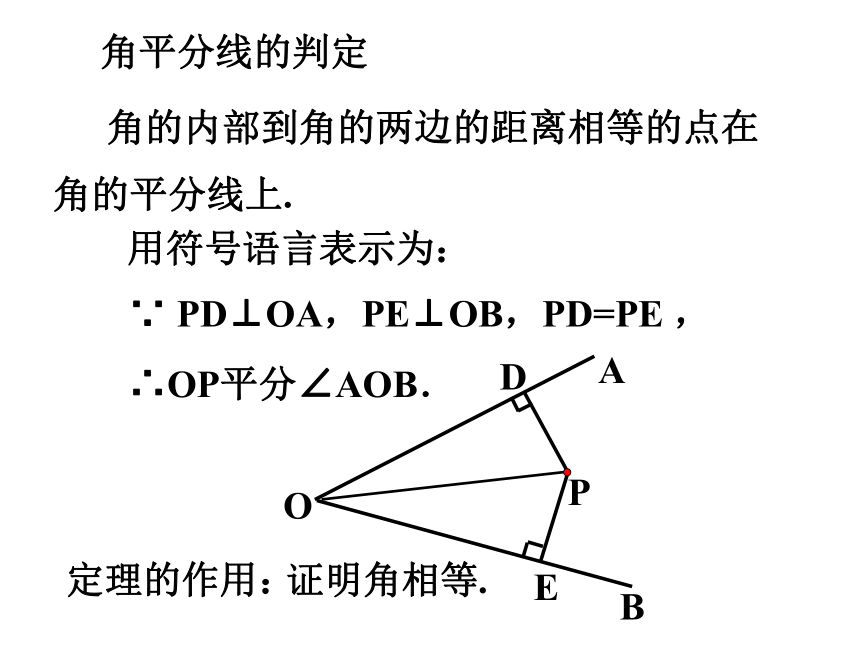
角的内部到角的两边的距离相等的点在角的平分线上.
∵ PD⊥OA,PE⊥OB,PD=PE ,
用符号语言表示为:
角平分线的判定
∴OP平分∠AOB.
B
A
D
O
P
E
定理的作用:
证明角相等.
线段垂直平分线上的点与这条线段两个端点的距离相等.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段垂直平分线的性质是解决线段相等问题的重要方法.
线段垂直平分线的判定可用来证明两线的垂直关系.
复习旧知
1.线段垂直平分线的性质定理
2.线段垂直平分线的判定定理
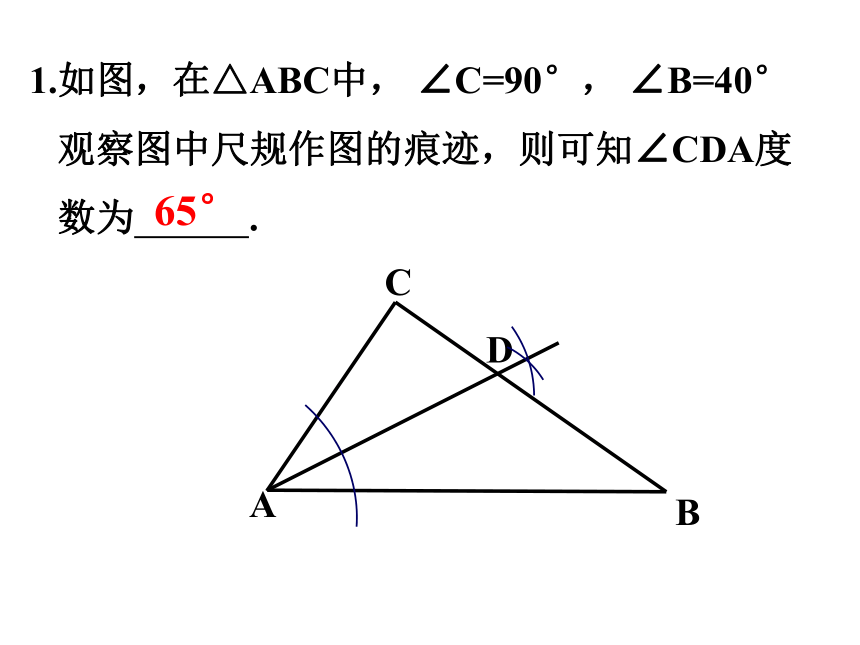
1.如图,在△ABC中, ∠C=90°, ∠B=40°
观察图中尺规作图的痕迹,则可知∠CDA度
数为 .
A
B
C
D
65°
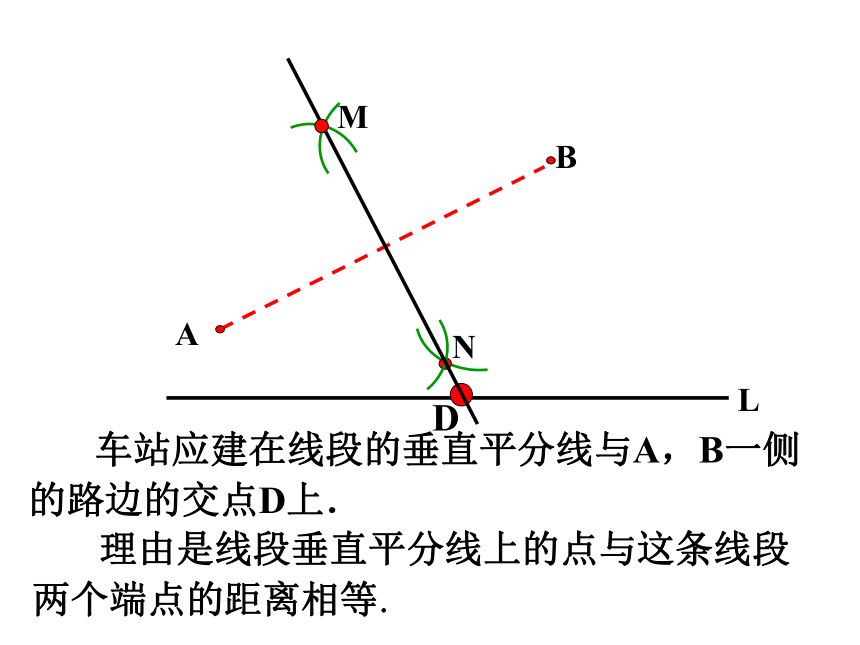
2. 如图,某地由于居民增多,要在公路L上增加一个公共汽车站,A、B是路边两个小区,这个公共汽车站建在什么位置,能使两个小区到车站的距离一样长?
L
A
B
车站应建在线段的垂直平分线与A,B一侧
的路边的交点D上.
理由是线段垂直平分线上的点与这条线段
两个端点的距离相等.
A
N
L
D
B
M
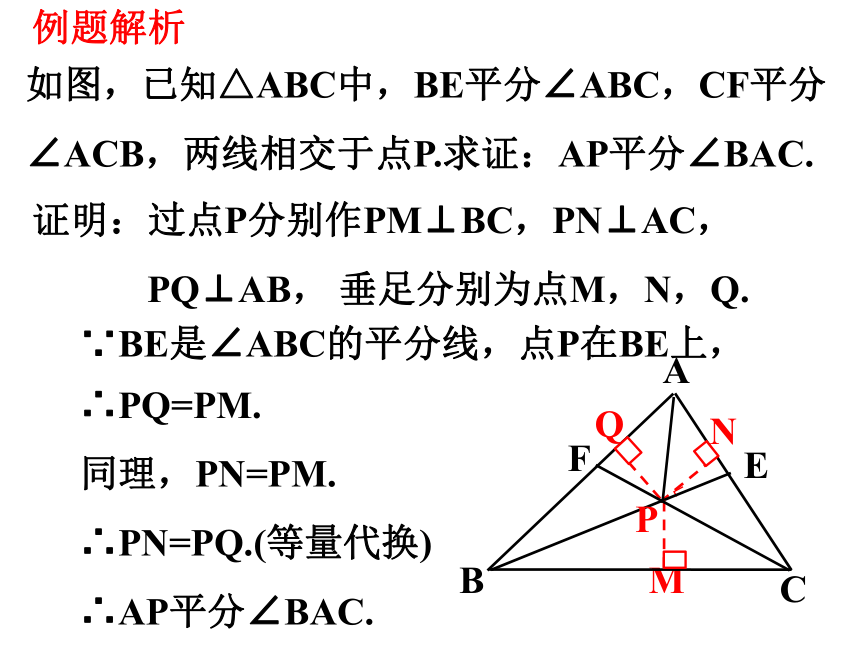
如图,已知△ABC中,BE平分∠ABC,CF平分
∠ACB,两线相交于点P.求证:AP平分∠BAC.
证明:过点P分别作PM⊥BC,PN⊥AC,
PQ⊥AB, 垂足分别为点M,N,Q.
∵BE是∠ABC的平分线,点P在BE上,
∴PQ=PM.
同理,PN=PM.
∴PN=PQ.(等量代换)
∴AP平分∠BAC.
例题解析
┐
N
Q
M
P
B
F
E
C
A
已知:如图,ΔABC中,∠ABC的平分线BE与
∠ACB的平分线CF相交于点P.
求证:AP平分∠BAC.
┐
这个例子说明:
三角形三条内角平分线相交于一点,这点到三角形三边的距离相等.
┐
N
Q
M
P
B
F
E
C
A
学习新知
例. 如图,电信部门要在S区建一座电视信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路m和n的距离也必须相等,发射塔应建在什么位置?在图上标出它的位置.
A
n
m
B
发射塔应建在线段AB的垂直平分线上.
发射塔要到两镇的距离相等,
发射塔应建在两公路夹角的平分线上.
发射塔要到两公路的距离相等,
A
n
发射塔
m
B
M
点M就是发射塔所在的位置.
解:
1.如图,在直线MN求作一点P,使点P到射线OA和OB的距离相等.
O
P
B
A
N
M
C
点P就是所求作的点.
学以致用
课堂小结
三角形的角平分线的性质定理的内容是什么?
它可以用来解决哪类几何问题?
你会用三角形角平分线的性质求三角形面积吗?
1. 如图,已知△ABC中,∠BCA=60°,点O到
三边的距离相等,则∠BOC等于( ).
B
O
C
A
36
巩固提高
A.120° B.125°
C.130° D.140°
2. 如图,已知△ABC中,CD是AB边上的高,
BE平分∠ABC,交CD于点E,BC=5,DE=2,
则△BEC的面积等于( ).
C
A.10° B.7
C.5 D.4
B
E
C
A
D
3. 如图,已知△ABC中,AB=AC,AD是BC的
中线,BE平分∠ABC,交AD于点E,AC=12,
DE=3, 则△ABE的面积等于( ).
B
A.16° B.18
C.32 D.36
B
E
C
A
D
4. 如图,已知△ABC的的三边AB,BC,CA的长
分别为60,70,50,它三条角平分线将△ABC
分成三个三角形,则S△ABO:S△BCO:S△ACO
等于( ).
B
O
C
A
D
A.1:1:1 B.1:2:3
C.5:6:7 D.6:7:5
5. 如图,已知△ABC中,∠C=90°,∠B=30°
AD平分∠BAC,DE⊥AB于点E,若DE=10,
则BC等于 .
B
D
C
A
E
30
6. 如图,已知△ABC的周长为24,OB,OC分别
平分∠ABC与∠ACB,OD⊥BC于点D,OD=3.
则△ABC的面积为 .
B
D
O
C
A
36
1.如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建
a
b
c
探究活动
2.到三角形三边所在的直线距离相等的点有几个?
各是如何找到的?
答:到三角形三边所在的直线距离相等的点有4个.
一个是三个内角的平分线交点(叫内心);
三个是三条外角平分线两两相交的交点(叫旁心).
今天作业
课本P147页第4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
15.4角的平分线 (3)
掌握三角形三条内角平分线相交于一点,这点到三角形三边的距离相等这一性质.
教学重点:
教学难点:
教学目标:
会应用三角形的角平分线的性质解题.
应用三角形的角平分线的性质解题.
P到OA的距离
P到OB的距离
角平分线上的点
符号语言:
∵ OC平分∠AOB,且PD⊥OA, PE⊥OB ,
∴ PD= PE.
角的平分线上的点到角的两边的距离相等.
角平分线的性质:
O
D
E
P
A
C
B
定理的作用:
证明线段相等.
复习旧知
角的内部到角的两边的距离相等的点在角的平分线上.
∵ PD⊥OA,PE⊥OB,PD=PE ,
用符号语言表示为:
角平分线的判定
∴OP平分∠AOB.
B
A
D
O
P
E
定理的作用:
证明角相等.
线段垂直平分线上的点与这条线段两个端点的距离相等.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
线段垂直平分线的性质是解决线段相等问题的重要方法.
线段垂直平分线的判定可用来证明两线的垂直关系.
复习旧知
1.线段垂直平分线的性质定理
2.线段垂直平分线的判定定理
1.如图,在△ABC中, ∠C=90°, ∠B=40°
观察图中尺规作图的痕迹,则可知∠CDA度
数为 .
A
B
C
D
65°
2. 如图,某地由于居民增多,要在公路L上增加一个公共汽车站,A、B是路边两个小区,这个公共汽车站建在什么位置,能使两个小区到车站的距离一样长?
L
A
B
车站应建在线段的垂直平分线与A,B一侧
的路边的交点D上.
理由是线段垂直平分线上的点与这条线段
两个端点的距离相等.
A
N
L
D
B
M
如图,已知△ABC中,BE平分∠ABC,CF平分
∠ACB,两线相交于点P.求证:AP平分∠BAC.
证明:过点P分别作PM⊥BC,PN⊥AC,
PQ⊥AB, 垂足分别为点M,N,Q.
∵BE是∠ABC的平分线,点P在BE上,
∴PQ=PM.
同理,PN=PM.
∴PN=PQ.(等量代换)
∴AP平分∠BAC.
例题解析
┐
N
Q
M
P
B
F
E
C
A
已知:如图,ΔABC中,∠ABC的平分线BE与
∠ACB的平分线CF相交于点P.
求证:AP平分∠BAC.
┐
这个例子说明:
三角形三条内角平分线相交于一点,这点到三角形三边的距离相等.
┐
N
Q
M
P
B
F
E
C
A
学习新知
例. 如图,电信部门要在S区建一座电视信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路m和n的距离也必须相等,发射塔应建在什么位置?在图上标出它的位置.
A
n
m
B
发射塔应建在线段AB的垂直平分线上.
发射塔要到两镇的距离相等,
发射塔应建在两公路夹角的平分线上.
发射塔要到两公路的距离相等,
A
n
发射塔
m
B
M
点M就是发射塔所在的位置.
解:
1.如图,在直线MN求作一点P,使点P到射线OA和OB的距离相等.
O
P
B
A
N
M
C
点P就是所求作的点.
学以致用
课堂小结
三角形的角平分线的性质定理的内容是什么?
它可以用来解决哪类几何问题?
你会用三角形角平分线的性质求三角形面积吗?
1. 如图,已知△ABC中,∠BCA=60°,点O到
三边的距离相等,则∠BOC等于( ).
B
O
C
A
36
巩固提高
A.120° B.125°
C.130° D.140°
2. 如图,已知△ABC中,CD是AB边上的高,
BE平分∠ABC,交CD于点E,BC=5,DE=2,
则△BEC的面积等于( ).
C
A.10° B.7
C.5 D.4
B
E
C
A
D
3. 如图,已知△ABC中,AB=AC,AD是BC的
中线,BE平分∠ABC,交AD于点E,AC=12,
DE=3, 则△ABE的面积等于( ).
B
A.16° B.18
C.32 D.36
B
E
C
A
D
4. 如图,已知△ABC的的三边AB,BC,CA的长
分别为60,70,50,它三条角平分线将△ABC
分成三个三角形,则S△ABO:S△BCO:S△ACO
等于( ).
B
O
C
A
D
A.1:1:1 B.1:2:3
C.5:6:7 D.6:7:5
5. 如图,已知△ABC中,∠C=90°,∠B=30°
AD平分∠BAC,DE⊥AB于点E,若DE=10,
则BC等于 .
B
D
C
A
E
30
6. 如图,已知△ABC的周长为24,OB,OC分别
平分∠ABC与∠ACB,OD⊥BC于点D,OD=3.
则△ABC的面积为 .
B
D
O
C
A
36
1.如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建
a
b
c
探究活动
2.到三角形三边所在的直线距离相等的点有几个?
各是如何找到的?
答:到三角形三边所在的直线距离相等的点有4个.
一个是三个内角的平分线交点(叫内心);
三个是三条外角平分线两两相交的交点(叫旁心).
今天作业
课本P147页第4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
