15.4 角的平分线 (2) 教学课件(共25张PPT)
文档属性
| 名称 | 15.4 角的平分线 (2) 教学课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 11:27:55 | ||
图片预览



文档简介
(共25张PPT)
15.4角的平分线 (2)
沪科版 八年级上册
掌握角平分线的性质和判定定理.
教学重点:
教学难点:
教学目标:
会应用角平分线的性质和判定定理解题.
应用角平分线的性质和判定定理解题.
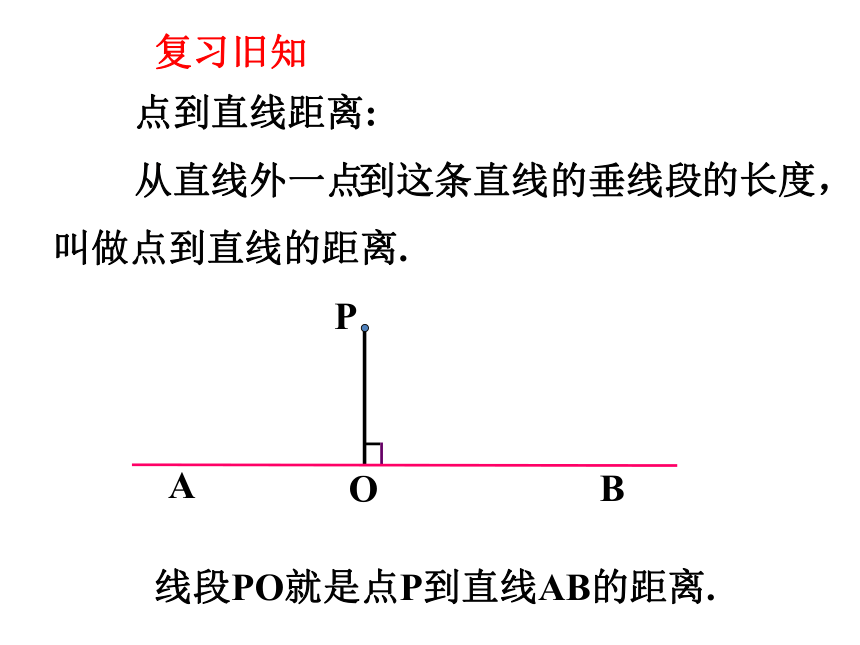
点到直线距离:
从直线外一点
到这条直线的垂线段
的长度,
叫做点到直线的距离.
O
P
A
B
线段PO就是点P到直线AB的距离.
复习旧知
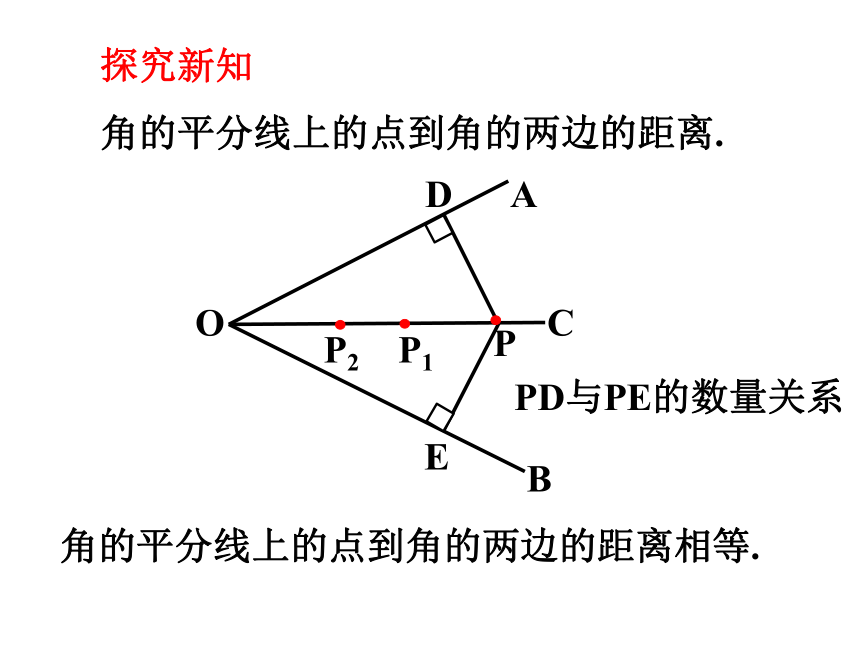
角的平分线上的点到角的两边的距离相等.
D
P
E
B
A
O
C
角的平分线上的点到角的两边的距离.
P1
P2
PD与PE的数量关系
探究新知
证明几何命题的一般步骤:
1.明确命题的已知和求证;
2.根据题意,画出图形,并用数学符号
表示已知和求证;
3.经过分析,找出由已知推出求证的途径,
写出证明过程.
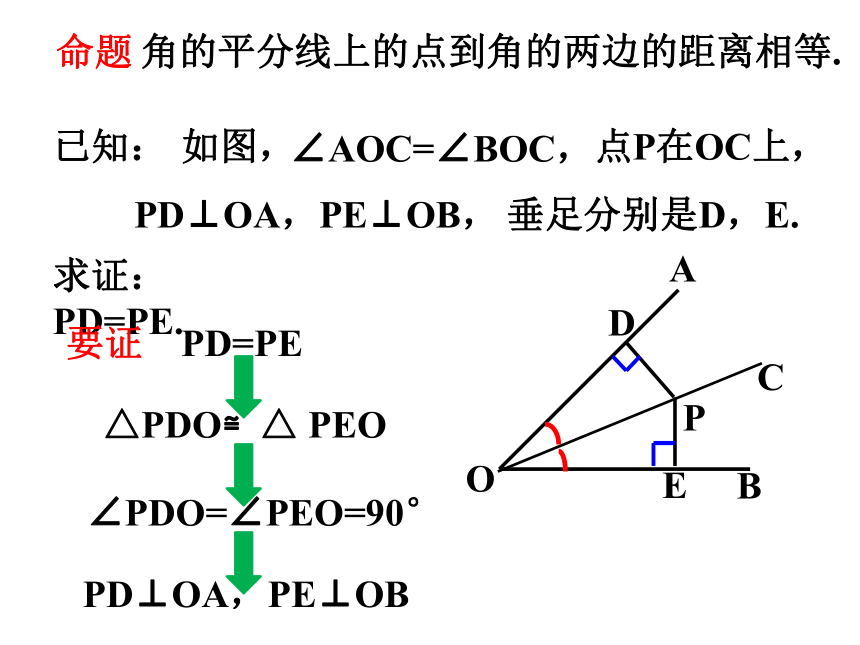
角的平分线上的点到角的两边的距离相等.
命题
∠AOC=∠BOC,
求证:PD=PE.
D
P
E
A
O
B
C
角的平分线上的点到角的两边的距离相等.
命题
PD=PE
△PDO≌△ PEO
∠PDO=∠PEO=90°
PD⊥OA,PE⊥OB
要证
已知:
如图,
点P在OC上,
PD⊥OA,PE⊥OB,
垂足分别是D,E.
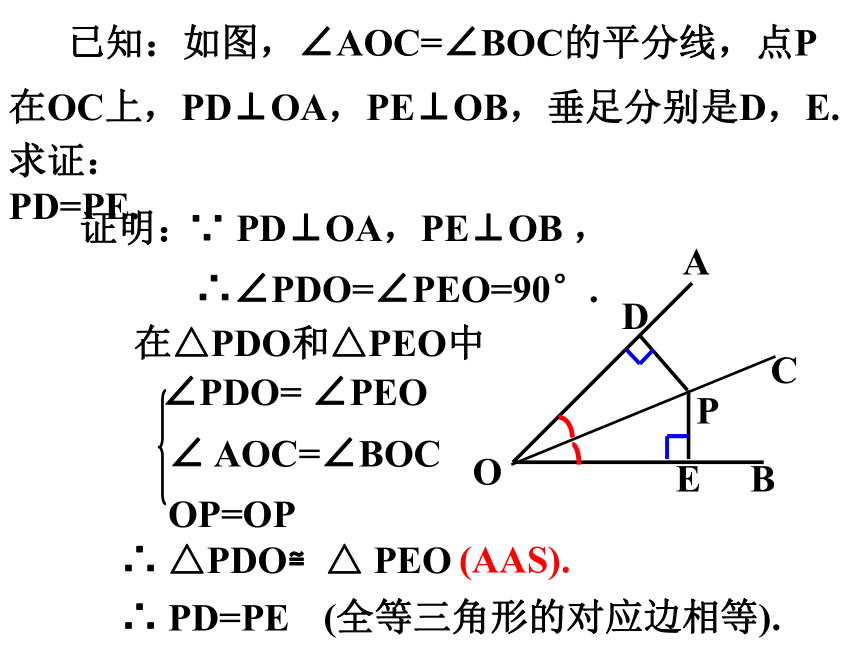
已知:如图,∠AOC=∠BOC的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.
证明:
在△PDO和△PEO中
∴ PD=PE
∠PDO= ∠PEO
∴ △PDO≌△ PEO
D
P
E
A
O
B
C
∵ PD⊥OA,PE⊥OB ,
∴∠PDO=∠PEO=90°.
(全等三角形的对应边相等).
(AAS).
∠ AOC=∠BOC
OP=OP
P到OA的距离
P到OB的距离
角平分线上的点
几何语言:
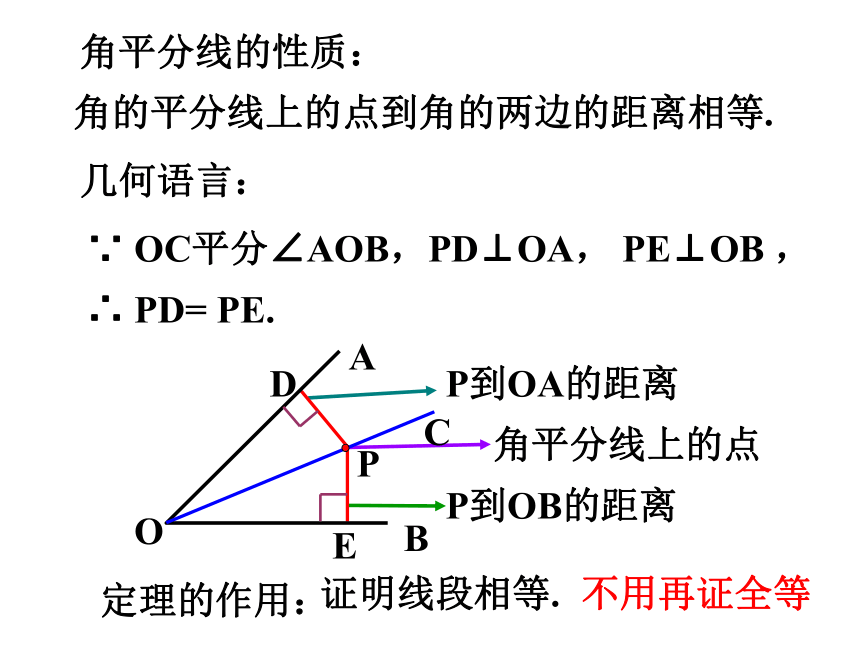
∵ OC平分∠AOB,PD⊥OA, PE⊥OB ,
∴ PD= PE.
角的平分线上的点到角的两边的距离相等.
角平分线的性质:
O
D
E
P
A
C
B
定理的作用:
证明线段相等.
不用再证全等
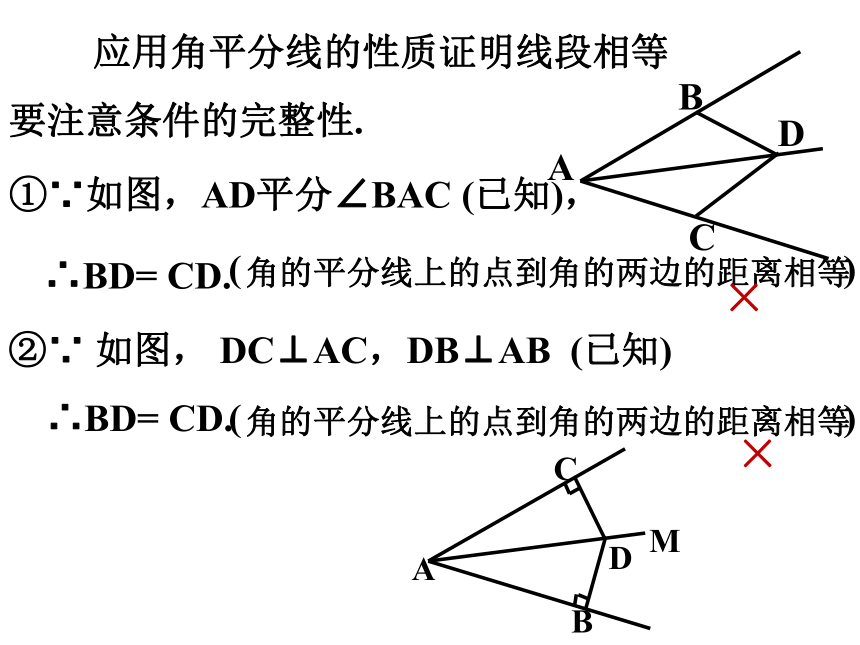
①∵如图,AD平分∠BAC (已知),
( )
角的平分线上的点到角的两边的距离相等
∴BD= CD.
C
A
D
B
应用角平分线的性质证明线段相等
要注意条件的完整性.
②∵ 如图, DC⊥AC,DB⊥AB (已知)
角的平分线上的点到角的两边的距离相等
∴BD= CD.
( )
C
A
D
B
M
×
×
1.如图, 点P在∠MON的平分线上,点P到
ON的距离等于10,点Q是射线OM的一个动点.
下列选项正确的是( ).
A.PQ<10 B.PQ>10
C.PQ≤10 D.PQ≥10
P
O
M
Q
N
D
练习巩固
2 .如图,在△ABC中,∠C=90°,∠ABC的平
分线BD交AC于点D.若AC=8cm,AD=5cm,则
点D到AB边的距离是 cm.
3
A
B
C
D
3.如图,已知点P是∠AOB的平分线OC上的一点,
PE⊥OA,垂足是E, PD∥OA,交OB于点D.
若OD=10cm,则PE= cm .
5
O
P
B
A
D
C
E
反过来,到一个角的两边的距离相等的点
是否一定在这个角的平分线上呢?
已知:如图, PD⊥OA,PE⊥OB,点D、E为垂足,PD=PE.
D
B
A
O
P
E
求证:点P在∠AOB的平分线上.
到角的两边的距离相等的点在这个角的平分线上.
探究新知
命题
已知:如图, PD⊥OA,PE⊥OB,点D、E为垂足,PD=PE.求证:点P在∠AOB的平分线上.
B
A
D
O
P
E
连接OP,
证明:
∵ PD⊥OA,PE⊥OB,
在Rt△PDO和Rt△PEO中,
PD=PE
∴ Rt△PDO≌Rt△PEO
∴ ∠ POD=∠POE.
∴OP是∠AOB的平分线,
∴ ∠PDO=∠PEO=90°.
PO=PO
(HL).
∴点P在∠AOB的平分线上.
P到OA的距离
P到OB的距离
点在角平分线上
几何语言:
∵ PD⊥OA, PE⊥OB ,
∴ OC平分∠AOB.
到角的两边的距离相等的点在这个角的平分线上.
角平分线的判定:
O
D
E
P
A
C
B
定理的作用:
证明角相等.
不用再证全等
PD= PE,
角的平分线的性质
图形
已知
结论
P
C
P
C
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
PD=PE
PD⊥OA于D
PE⊥OB于E
角的平分线的判定
认识新知
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
过点P作PD⊥AB于D,
如图,△ABC的角平分线BM,CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
D
P
M
N
A
B
C
F
E
证明:
PE⊥BC于E,
PF⊥AC于F.
例题解析
1.如图,已知DB⊥AE,DC⊥AF,垂足分别是B,
C.DB=DC,∠BAC=40°,∠ADG=130°,
则∠DGF的度数是 .
E
F
B
A
D
C
G
150°
学以致用
2.如图,△ABC的外角平分线BD,CE相交于点P.求证:点P到三边AB、BC、CA的距离相等.
E
P
B
A
D
C
∵BD是∠ABC的外角平分线,点P在BD上,
∴PF=PM.
同理,PM=PN.
∴PF=PM=PN.
即点P到三边AB、BC、
CA的距离相等.
过点P作PF⊥AB于F,
证明:
PM⊥BC于M,
PN⊥AC于N.
F
M
N
课堂小结
1.角平分线的性质定理的内容是什么?
它可以用来解决哪类几何问题?
2.角平分线的判定定理的内容是什么?
它可以用来解决哪类几何问题?
1.如图,在Rt△ABC中,∠C=90°, 观察图中
尺规作图的痕迹,若CG=2, P为AB上一动点,
则GP的最小值为( ).
A
B
C
D
E
G
P
F
A. 4 B. 3 C. 2 D. 1
C
巩固提高
2.如图,已知点D是∠AOB的平分线上的一点,
DC⊥OB,垂足是C, DE∥OB,交OA于点E.
若∠ AOB=30°,DC=5cm,则OE= cm .
10
O
B
A
D
C
E
今天作业
课本P146页第1、2题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
15.4角的平分线 (2)
沪科版 八年级上册
掌握角平分线的性质和判定定理.
教学重点:
教学难点:
教学目标:
会应用角平分线的性质和判定定理解题.
应用角平分线的性质和判定定理解题.
点到直线距离:
从直线外一点
到这条直线的垂线段
的长度,
叫做点到直线的距离.
O
P
A
B
线段PO就是点P到直线AB的距离.
复习旧知
角的平分线上的点到角的两边的距离相等.
D
P
E
B
A
O
C
角的平分线上的点到角的两边的距离.
P1
P2
PD与PE的数量关系
探究新知
证明几何命题的一般步骤:
1.明确命题的已知和求证;
2.根据题意,画出图形,并用数学符号
表示已知和求证;
3.经过分析,找出由已知推出求证的途径,
写出证明过程.
角的平分线上的点到角的两边的距离相等.
命题
∠AOC=∠BOC,
求证:PD=PE.
D
P
E
A
O
B
C
角的平分线上的点到角的两边的距离相等.
命题
PD=PE
△PDO≌△ PEO
∠PDO=∠PEO=90°
PD⊥OA,PE⊥OB
要证
已知:
如图,
点P在OC上,
PD⊥OA,PE⊥OB,
垂足分别是D,E.
已知:如图,∠AOC=∠BOC的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.
证明:
在△PDO和△PEO中
∴ PD=PE
∠PDO= ∠PEO
∴ △PDO≌△ PEO
D
P
E
A
O
B
C
∵ PD⊥OA,PE⊥OB ,
∴∠PDO=∠PEO=90°.
(全等三角形的对应边相等).
(AAS).
∠ AOC=∠BOC
OP=OP
P到OA的距离
P到OB的距离
角平分线上的点
几何语言:
∵ OC平分∠AOB,PD⊥OA, PE⊥OB ,
∴ PD= PE.
角的平分线上的点到角的两边的距离相等.
角平分线的性质:
O
D
E
P
A
C
B
定理的作用:
证明线段相等.
不用再证全等
①∵如图,AD平分∠BAC (已知),
( )
角的平分线上的点到角的两边的距离相等
∴BD= CD.
C
A
D
B
应用角平分线的性质证明线段相等
要注意条件的完整性.
②∵ 如图, DC⊥AC,DB⊥AB (已知)
角的平分线上的点到角的两边的距离相等
∴BD= CD.
( )
C
A
D
B
M
×
×
1.如图, 点P在∠MON的平分线上,点P到
ON的距离等于10,点Q是射线OM的一个动点.
下列选项正确的是( ).
A.PQ<10 B.PQ>10
C.PQ≤10 D.PQ≥10
P
O
M
Q
N
D
练习巩固
2 .如图,在△ABC中,∠C=90°,∠ABC的平
分线BD交AC于点D.若AC=8cm,AD=5cm,则
点D到AB边的距离是 cm.
3
A
B
C
D
3.如图,已知点P是∠AOB的平分线OC上的一点,
PE⊥OA,垂足是E, PD∥OA,交OB于点D.
若OD=10cm,则PE= cm .
5
O
P
B
A
D
C
E
反过来,到一个角的两边的距离相等的点
是否一定在这个角的平分线上呢?
已知:如图, PD⊥OA,PE⊥OB,点D、E为垂足,PD=PE.
D
B
A
O
P
E
求证:点P在∠AOB的平分线上.
到角的两边的距离相等的点在这个角的平分线上.
探究新知
命题
已知:如图, PD⊥OA,PE⊥OB,点D、E为垂足,PD=PE.求证:点P在∠AOB的平分线上.
B
A
D
O
P
E
连接OP,
证明:
∵ PD⊥OA,PE⊥OB,
在Rt△PDO和Rt△PEO中,
PD=PE
∴ Rt△PDO≌Rt△PEO
∴ ∠ POD=∠POE.
∴OP是∠AOB的平分线,
∴ ∠PDO=∠PEO=90°.
PO=PO
(HL).
∴点P在∠AOB的平分线上.
P到OA的距离
P到OB的距离
点在角平分线上
几何语言:
∵ PD⊥OA, PE⊥OB ,
∴ OC平分∠AOB.
到角的两边的距离相等的点在这个角的平分线上.
角平分线的判定:
O
D
E
P
A
C
B
定理的作用:
证明角相等.
不用再证全等
PD= PE,
角的平分线的性质
图形
已知
结论
P
C
P
C
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
PD=PE
PD⊥OA于D
PE⊥OB于E
角的平分线的判定
认识新知
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
过点P作PD⊥AB于D,
如图,△ABC的角平分线BM,CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.
D
P
M
N
A
B
C
F
E
证明:
PE⊥BC于E,
PF⊥AC于F.
例题解析
1.如图,已知DB⊥AE,DC⊥AF,垂足分别是B,
C.DB=DC,∠BAC=40°,∠ADG=130°,
则∠DGF的度数是 .
E
F
B
A
D
C
G
150°
学以致用
2.如图,△ABC的外角平分线BD,CE相交于点P.求证:点P到三边AB、BC、CA的距离相等.
E
P
B
A
D
C
∵BD是∠ABC的外角平分线,点P在BD上,
∴PF=PM.
同理,PM=PN.
∴PF=PM=PN.
即点P到三边AB、BC、
CA的距离相等.
过点P作PF⊥AB于F,
证明:
PM⊥BC于M,
PN⊥AC于N.
F
M
N
课堂小结
1.角平分线的性质定理的内容是什么?
它可以用来解决哪类几何问题?
2.角平分线的判定定理的内容是什么?
它可以用来解决哪类几何问题?
1.如图,在Rt△ABC中,∠C=90°, 观察图中
尺规作图的痕迹,若CG=2, P为AB上一动点,
则GP的最小值为( ).
A
B
C
D
E
G
P
F
A. 4 B. 3 C. 2 D. 1
C
巩固提高
2.如图,已知点D是∠AOB的平分线上的一点,
DC⊥OB,垂足是C, DE∥OB,交OA于点E.
若∠ AOB=30°,DC=5cm,则OE= cm .
10
O
B
A
D
C
E
今天作业
课本P146页第1、2题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
