人教版九年级下册 27.1 图形的相似 教学课件(共37张PPT)
文档属性
| 名称 | 人教版九年级下册 27.1 图形的相似 教学课件(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 11.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 14:47:04 | ||
图片预览







文档简介
(共37张PPT)
27.1 图形的相似
第二十七章 相 似
形状相同,大小也相同.
什么样的图形是全等形?
知识回顾
1.能通过生活中的实例认识图形的相似,通过观察直观地判断两个图形是否相似.
2.了解成比例线段的概念.
学习目标
3.理解相似多边形的定义.
4.能根据多边形相似进行相关的计算,会根据条件判断两个多边形是否相似.
5.在学习相似图形的过程中,提高对相似图形中的对应关系的认识,增强数学推理能力.
学习目标
全等!
下图中的两个图形有什么关系?
课堂导入
全等满足什么条件呢?
大小不同,不全等!
如果把其中的一片树叶缩小,它们还全等吗?
下面的每组图形有什么相同和不同的地方?
知识点1:相似图形
新知探究
相同点:形状相同
不同点:大小不同
我们把形状相同的图形叫相似图形.
定义:
注意:两个图形是否相似与图形的大小、位置无关.
巧学妙计:
相似图形形状同,大小位置均无关;
相似图形有特例,全等属于相似形.
新知探究
1. 图形的放大:
相似图形的关系:
相似图形的关系:
2. 图形的缩小:
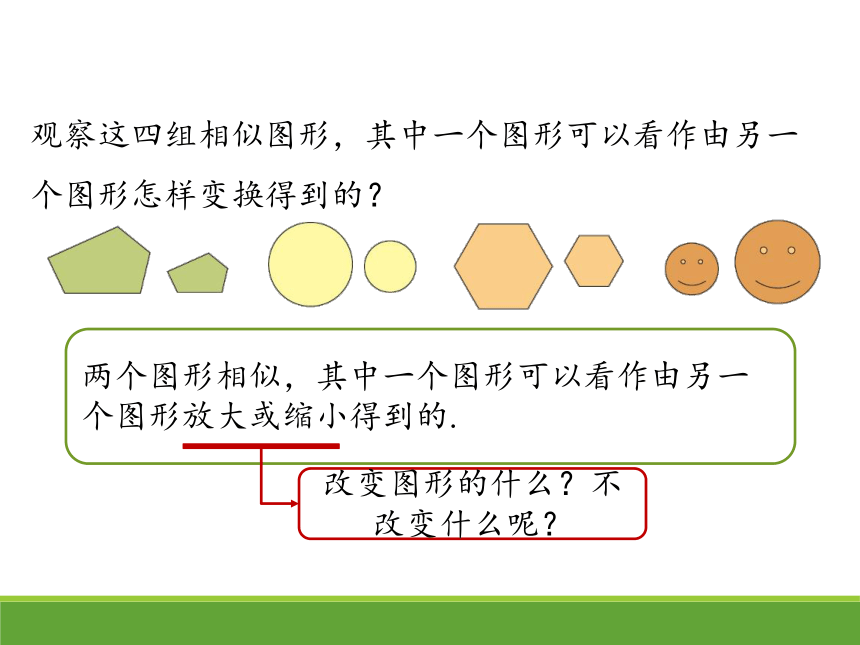
观察这四组相似图形,其中一个图形可以看作由另一个图形怎样变换得到的?
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到的.
改变图形的什么?不改变什么呢?
你还知道哪些相似图形?
放电影时,银幕上的画面与胶片上的画面是相似图形.
复印机把一个图形放大,放大后的图形与原来的图形是相似图形.
实际的建筑物与它的模型是相似图形.
国旗上的大五角星与小五角星是相似图形吗?四颗小五角星呢?
全等图形是特殊的相似图形,也就是说全等图形一定是相似图形,但相似图形不一定是全等图形.
你见过哈哈镜吗?哈哈镜与平面镜中的形象哪一个与你本人相似?
思考:
放大镜下的图形和原来的图形相似吗?
练一练
放大镜下的角与原图
形中角是什么关系
对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度的比)与另两条线段的比相等,
如 (即ad=bc),我们就说这四条线段成比例.
新知探究
知识点2:比例线段
例1 下列四组长度中的四条线段能成比例的是( )
典例精析
A. 1 cm,2 cm,3 cm,4 cm
B. 2 cm,4 cm,6 cm,8 cm
C. 5 cm,30 cm,10 cm,15 cm
D. 5 cm,10 cm,15 cm,20 cm
c
判断四条线段是否成比例的方法
首先统一单位,并把四条线段按从小到大(或从大到小)的顺序排列,然后计算并判断.计算的方法有两种:
(1)计算前两条线段的比和后两条线段的比,若比值相等,则这四条线段成比例;
(2)分别计算第一条线段与第四条线段的乘积、第二条线段与第三条线段的乘积,如果乘积相同,则这四条线段成比例.
A
代入法
参数法
利用比例的性质求代数式的值的方法
(1)代入法,用含有其中一个字母的代数式表示其他字母,然后代入求值;
(2)参数法,即先根据比例式设出合适的参数,然后用含此参数的代数式表示出相应的字母,再代入求值.
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
多边形 ABCDEF 是显示在电脑屏幕上的,而多边形 A1B1C1D1E1F1 是投射到银幕上的.
观察与思考
新知探究
知识点3:相似多边形与相似比
问题1 这两个多边形相似吗?
问题2 在这两个多边形中,是否有对应相等的内角?
问题3 在这两个多边形中,夹相等内角的两边是否 成比例?
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的特征:
相似多边形的定义:
归纳:
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
议一议
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
…
a1
a2
a3
an
思考:
任意的两个菱形(或矩形)是否相似?为什么?
例2 如图,四边形 ABCD 和 EFGH 相似,求角α,β的大小和EH的长度 x.
典例精析
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
在四边形ABCD中,
β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,∴ 它们的对
应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
∵ 四边形ABCD和四边形EFGH相似,∴它们的对应边成比
例,由此可得
解得 x = 28 cm.
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
相似图形
形状相同的图形叫做相似图形
相似图形的大小不一定相同
相似多边形对应边的比叫做相似比
对应角相等,对应边成比例
课堂小结
图形的相似
相似多边形
如图所示的两个五边形相似,求未知边 a,b, c,d 的长度.
5
3
2
c
d
7.5
b
a
6
9
练一练
解:相似多边形的对应边的比相等,由此可得
解得:a=3,b=4.5,c=4,d=6.
所以未知边a,b,c,d的长度分别为3,4.5,4,6.
, , , ,
当堂练习
1. 下列图形中能够确定相似的是[多选] ( )
A.两个半径不相等的圆 B.所有的等边三角形
C.所有的等腰三角形 D.所有的正方形
E.所有的等腰梯形 F.所有的正六边形
ABDF
2. 若一张地图的比例尺是 1:150000,在地图上量得
甲、乙两地的距离是 5 cm,则甲、乙两地的实际
距离是 ( )
A. 3000 m B. 3500 m
C. 5000 m D. 7500 m
D
3. 如图所示的两个四边形是否相似?
答案:不相似.
4. 观察下面的图形 (a)~(e),其中哪些是与图形 (1)或
(2) 相似的?
5. 填空:
(1) 如图①是两个相似的四边
形,则x= ,y = ,
α= ;
(2) 如图②是两个相似的矩形,
x= .
╰
65°
╯
80°
α
╭
6
125°
╯
80°
╮
3
x
y
图①
3
5
30
20
15
x
图②
2.5
1.5
90°
22.5
6. 如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1.
(1) 求BC的长;
A
B
C
D
E
F
解:∵ E 是 AD 的中点,
∴ .
又∵矩形 ABCD 与矩形 EABF
相似,AB=1,
∴ ,
∴ AB2 = AE·BC,
∴ .
解得
(2) 求矩形 ABEF 与矩形 ABCD 的相似比.
A
B
C
D
E
F
解:矩形 ABEF 与矩形 ABCD
的相似比为:
27.1 图形的相似
第二十七章 相 似
形状相同,大小也相同.
什么样的图形是全等形?
知识回顾
1.能通过生活中的实例认识图形的相似,通过观察直观地判断两个图形是否相似.
2.了解成比例线段的概念.
学习目标
3.理解相似多边形的定义.
4.能根据多边形相似进行相关的计算,会根据条件判断两个多边形是否相似.
5.在学习相似图形的过程中,提高对相似图形中的对应关系的认识,增强数学推理能力.
学习目标
全等!
下图中的两个图形有什么关系?
课堂导入
全等满足什么条件呢?
大小不同,不全等!
如果把其中的一片树叶缩小,它们还全等吗?
下面的每组图形有什么相同和不同的地方?
知识点1:相似图形
新知探究
相同点:形状相同
不同点:大小不同
我们把形状相同的图形叫相似图形.
定义:
注意:两个图形是否相似与图形的大小、位置无关.
巧学妙计:
相似图形形状同,大小位置均无关;
相似图形有特例,全等属于相似形.
新知探究
1. 图形的放大:
相似图形的关系:
相似图形的关系:
2. 图形的缩小:
观察这四组相似图形,其中一个图形可以看作由另一个图形怎样变换得到的?
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到的.
改变图形的什么?不改变什么呢?
你还知道哪些相似图形?
放电影时,银幕上的画面与胶片上的画面是相似图形.
复印机把一个图形放大,放大后的图形与原来的图形是相似图形.
实际的建筑物与它的模型是相似图形.
国旗上的大五角星与小五角星是相似图形吗?四颗小五角星呢?
全等图形是特殊的相似图形,也就是说全等图形一定是相似图形,但相似图形不一定是全等图形.
你见过哈哈镜吗?哈哈镜与平面镜中的形象哪一个与你本人相似?
思考:
放大镜下的图形和原来的图形相似吗?
练一练
放大镜下的角与原图
形中角是什么关系
对于四条线段a、b、c、d,如果其中两条线段的比(即它们的长度的比)与另两条线段的比相等,
如 (即ad=bc),我们就说这四条线段成比例.
新知探究
知识点2:比例线段
例1 下列四组长度中的四条线段能成比例的是( )
典例精析
A. 1 cm,2 cm,3 cm,4 cm
B. 2 cm,4 cm,6 cm,8 cm
C. 5 cm,30 cm,10 cm,15 cm
D. 5 cm,10 cm,15 cm,20 cm
c
判断四条线段是否成比例的方法
首先统一单位,并把四条线段按从小到大(或从大到小)的顺序排列,然后计算并判断.计算的方法有两种:
(1)计算前两条线段的比和后两条线段的比,若比值相等,则这四条线段成比例;
(2)分别计算第一条线段与第四条线段的乘积、第二条线段与第三条线段的乘积,如果乘积相同,则这四条线段成比例.
A
代入法
参数法
利用比例的性质求代数式的值的方法
(1)代入法,用含有其中一个字母的代数式表示其他字母,然后代入求值;
(2)参数法,即先根据比例式设出合适的参数,然后用含此参数的代数式表示出相应的字母,再代入求值.
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
多边形 ABCDEF 是显示在电脑屏幕上的,而多边形 A1B1C1D1E1F1 是投射到银幕上的.
观察与思考
新知探究
知识点3:相似多边形与相似比
问题1 这两个多边形相似吗?
问题2 在这两个多边形中,是否有对应相等的内角?
问题3 在这两个多边形中,夹相等内角的两边是否 成比例?
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
各角分别相等、各边成比例的两个多边形叫做相似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的特征:
相似多边形的定义:
归纳:
任意两个等边三角形相似吗?任意两个正方形呢?任意两个正 n 边形呢?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
议一议
同理,任意两个正方形都相似.
归纳:任意两个边数相等的正多边形都相似.
…
a1
a2
a3
an
思考:
任意的两个菱形(或矩形)是否相似?为什么?
例2 如图,四边形 ABCD 和 EFGH 相似,求角α,β的大小和EH的长度 x.
典例精析
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
在四边形ABCD中,
β=360°-(78°+83°+118°)=81°.
∠α=∠C=83°,∠A=∠E=118°.
解:∵ 四边形 ABCD 和 EFGH 相似,∴ 它们的对
应角相等.由此可得
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
∵ 四边形ABCD和四边形EFGH相似,∴它们的对应边成比
例,由此可得
解得 x = 28 cm.
,即 .
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
相似图形
形状相同的图形叫做相似图形
相似图形的大小不一定相同
相似多边形对应边的比叫做相似比
对应角相等,对应边成比例
课堂小结
图形的相似
相似多边形
如图所示的两个五边形相似,求未知边 a,b, c,d 的长度.
5
3
2
c
d
7.5
b
a
6
9
练一练
解:相似多边形的对应边的比相等,由此可得
解得:a=3,b=4.5,c=4,d=6.
所以未知边a,b,c,d的长度分别为3,4.5,4,6.
, , , ,
当堂练习
1. 下列图形中能够确定相似的是[多选] ( )
A.两个半径不相等的圆 B.所有的等边三角形
C.所有的等腰三角形 D.所有的正方形
E.所有的等腰梯形 F.所有的正六边形
ABDF
2. 若一张地图的比例尺是 1:150000,在地图上量得
甲、乙两地的距离是 5 cm,则甲、乙两地的实际
距离是 ( )
A. 3000 m B. 3500 m
C. 5000 m D. 7500 m
D
3. 如图所示的两个四边形是否相似?
答案:不相似.
4. 观察下面的图形 (a)~(e),其中哪些是与图形 (1)或
(2) 相似的?
5. 填空:
(1) 如图①是两个相似的四边
形,则x= ,y = ,
α= ;
(2) 如图②是两个相似的矩形,
x= .
╰
65°
╯
80°
α
╭
6
125°
╯
80°
╮
3
x
y
图①
3
5
30
20
15
x
图②
2.5
1.5
90°
22.5
6. 如图,把矩形 ABCD 对折,折痕为 EF,若矩形ABCD 与矩形 EABF 相似,AB = 1.
(1) 求BC的长;
A
B
C
D
E
F
解:∵ E 是 AD 的中点,
∴ .
又∵矩形 ABCD 与矩形 EABF
相似,AB=1,
∴ ,
∴ AB2 = AE·BC,
∴ .
解得
(2) 求矩形 ABEF 与矩形 ABCD 的相似比.
A
B
C
D
E
F
解:矩形 ABEF 与矩形 ABCD
的相似比为:
