人教版九年级数学下册26.1.1《反比例函数》 教学方案(表格式)
文档属性
| 名称 | 人教版九年级数学下册26.1.1《反比例函数》 教学方案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 213.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 00:00:00 | ||
图片预览

文档简介
第二十六章 反比例函数
26.1.1反比例函数
一、 教学目标
1. 经历在实际问题中提炼出具有反比例变化规律的数字表达式;
2. 能识别反比例函数的常见形式;
3. 利用待定系数法求解反比例函数的解析式;
4. 理解反比例函数的描述现实世界中的重要意义.
二、 教学重难点
重点:反比例函数概念的理解;
难点:待定系数法求解反比例函数的解析式.
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
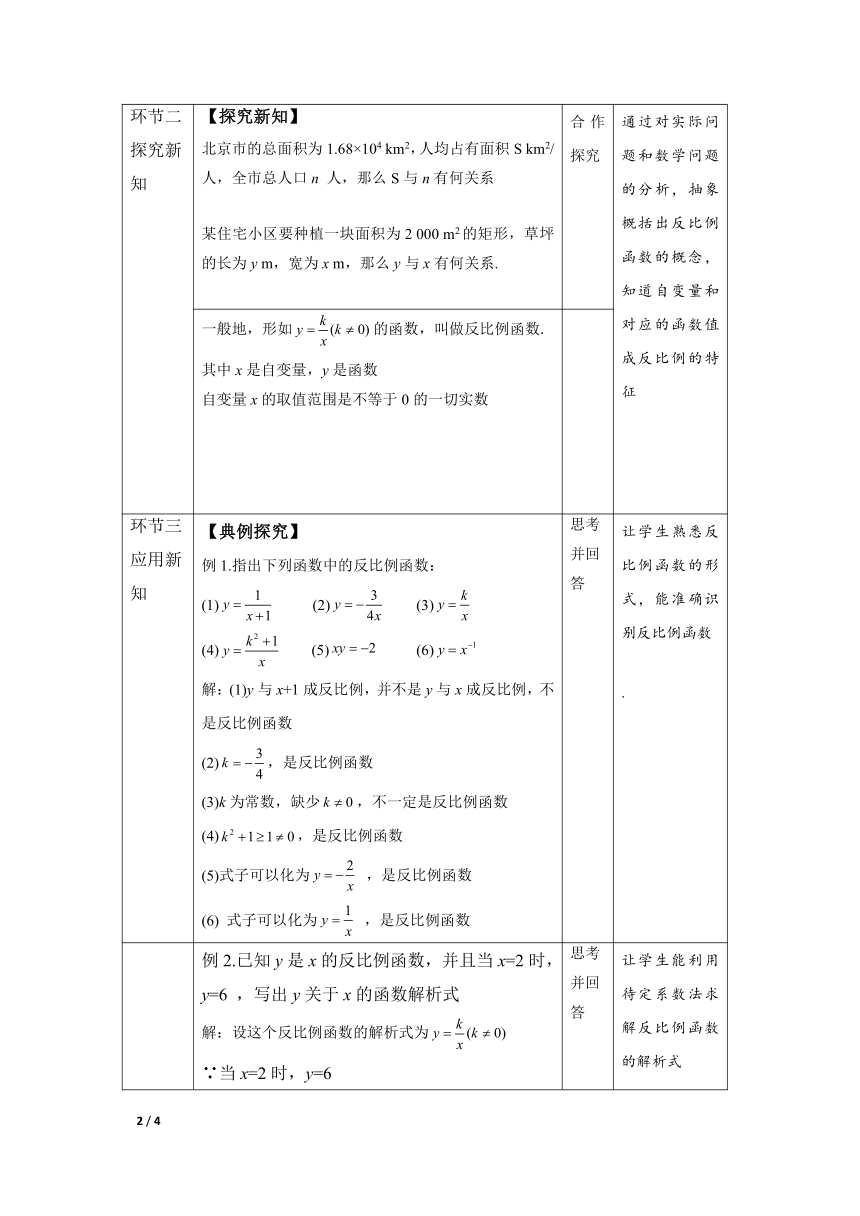
环节一 创设情景 【情景导入】 理解与回顾反比例关系和函数关系 通过对现实生活和数学中问题的分析,发现变量间的反比例关系和函数关系.
环节二 探究新知 【探究新知】 北京市的总面积为1.68×104 km2,人均占有面积S km2/人,全市总人口n 人,那么S与n有何关系 某住宅小区要种植一块面积为2 000 m2的矩形,草坪的长为y m,宽为x m,那么y与x有何关系. 合作探究 通过对实际问题和数学问题的分析,抽象概括出反比例函数的概念,知道自变量和对应的函数值成反比例的特征
一般地,形如的函数,叫做反比例函数. 其中x是自变量,y是函数 自变量x的取值范围是不等于0的一切实数
环节三 应用新知 【典例探究】 例1.指出下列函数中的反比例函数: (1) (2) (3) (4) (5) (6) 解:(1)y与x+1成反比例,并不是y与x成反比例,不是反比例函数 (2),是反比例函数 (3)k为常数,缺少,不一定是反比例函数 (4),是反比例函数 (5)式子可以化为 ,是反比例函数 (6) 式子可以化为 ,是反比例函数 思考并回答 让学生熟悉反比例函数的形式,能准确识别反比例函数 .
例2.已知y是x的反比例函数,并且当x=2时,y=6 ,写出y关于x的函数解析式 解:设这个反比例函数的解析式为 ∵当x=2时,y=6 ∴ ,解得:k=12 ∴这个反比例函数的解析为 思考并回答 让学生能利用待定系数法求解反比例函数的解析式
环节四 巩固新知 【随堂练习】 练1.指出下列函数中的反比例函数: (1) (2) (3) (4) (5) (6) 解:(1)y与x不是反比例,不是反比例函数 (2)y与成反比例,y与x不成反比例,不是反比例函数 (3),是反比例函数 (4),是反比例函数 (5)式子可以化为 ,是反比例函数 (6) 式子可以化为 ,是反比例函数 练习 通过课堂练习巩固新知,加深对反比例函数的识别
练2.已知y是关于x的反比例函数,当x=3时,y=2,求这个函数的表达式 解:设这个反比例函数的解析式为 ∵当x=3时,y=2 ∴ ,解得:k=6 ∴这个反比例函数的解析为 练习 通过课堂练习巩固新知,加深利用待定系数法求解函数解析式
练3.已知y与x+2成反比例,且当x=-1时,y = 3. (1)求y与x之间的函数解析式; (2)当 x = 0 时,求y的值. 解:(1)∵y与x+2成反比例 ∴设函数的解析式为 ∵当时,y = 3 ∴ ,解得:k = 3 ∴这个函数的解析式为 (2) ∵x = 0 ∴ 练习 通过课堂练习巩固新知,加深待定系数法的运用并理解反比例关系与反比例函数的区别
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 巩固例题练习 教科书第3页 习题1、2、3. 课后完成练习
4 / 5
26.1.1反比例函数
一、 教学目标
1. 经历在实际问题中提炼出具有反比例变化规律的数字表达式;
2. 能识别反比例函数的常见形式;
3. 利用待定系数法求解反比例函数的解析式;
4. 理解反比例函数的描述现实世界中的重要意义.
二、 教学重难点
重点:反比例函数概念的理解;
难点:待定系数法求解反比例函数的解析式.
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
环节一 创设情景 【情景导入】 理解与回顾反比例关系和函数关系 通过对现实生活和数学中问题的分析,发现变量间的反比例关系和函数关系.
环节二 探究新知 【探究新知】 北京市的总面积为1.68×104 km2,人均占有面积S km2/人,全市总人口n 人,那么S与n有何关系 某住宅小区要种植一块面积为2 000 m2的矩形,草坪的长为y m,宽为x m,那么y与x有何关系. 合作探究 通过对实际问题和数学问题的分析,抽象概括出反比例函数的概念,知道自变量和对应的函数值成反比例的特征
一般地,形如的函数,叫做反比例函数. 其中x是自变量,y是函数 自变量x的取值范围是不等于0的一切实数
环节三 应用新知 【典例探究】 例1.指出下列函数中的反比例函数: (1) (2) (3) (4) (5) (6) 解:(1)y与x+1成反比例,并不是y与x成反比例,不是反比例函数 (2),是反比例函数 (3)k为常数,缺少,不一定是反比例函数 (4),是反比例函数 (5)式子可以化为 ,是反比例函数 (6) 式子可以化为 ,是反比例函数 思考并回答 让学生熟悉反比例函数的形式,能准确识别反比例函数 .
例2.已知y是x的反比例函数,并且当x=2时,y=6 ,写出y关于x的函数解析式 解:设这个反比例函数的解析式为 ∵当x=2时,y=6 ∴ ,解得:k=12 ∴这个反比例函数的解析为 思考并回答 让学生能利用待定系数法求解反比例函数的解析式
环节四 巩固新知 【随堂练习】 练1.指出下列函数中的反比例函数: (1) (2) (3) (4) (5) (6) 解:(1)y与x不是反比例,不是反比例函数 (2)y与成反比例,y与x不成反比例,不是反比例函数 (3),是反比例函数 (4),是反比例函数 (5)式子可以化为 ,是反比例函数 (6) 式子可以化为 ,是反比例函数 练习 通过课堂练习巩固新知,加深对反比例函数的识别
练2.已知y是关于x的反比例函数,当x=3时,y=2,求这个函数的表达式 解:设这个反比例函数的解析式为 ∵当x=3时,y=2 ∴ ,解得:k=6 ∴这个反比例函数的解析为 练习 通过课堂练习巩固新知,加深利用待定系数法求解函数解析式
练3.已知y与x+2成反比例,且当x=-1时,y = 3. (1)求y与x之间的函数解析式; (2)当 x = 0 时,求y的值. 解:(1)∵y与x+2成反比例 ∴设函数的解析式为 ∵当时,y = 3 ∴ ,解得:k = 3 ∴这个函数的解析式为 (2) ∵x = 0 ∴ 练习 通过课堂练习巩固新知,加深待定系数法的运用并理解反比例关系与反比例函数的区别
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 巩固例题练习 教科书第3页 习题1、2、3. 课后完成练习
4 / 5
