人教版九年级数学下册28.2.2解直角三角形应用举例第2课时 教学方案(表格式)
文档属性
| 名称 | 人教版九年级数学下册28.2.2解直角三角形应用举例第2课时 教学方案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 261.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 00:00:00 | ||
图片预览

文档简介
第二十八章 锐角三角函数
28.2.2应用举例
第2课时
一、 教学目标
1.能够把解直角三角形相关知识应用到实际问题中;
2.能从实际问题中构造直角三角形,把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题;
3.经历从实际问题到数学问题的思考,培养学生数学建模思想和分析问题、解决问题的能力;
4.体会数学在解决实际问题中的应用,使学生感受数学在航海方面的应用,使学生感受到数学的广泛作用.
二、 教学重难点
重点:能够把解直角三角形相关知识应用到实际问题中.
难点:灵活选择三角函数解决问题.
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
环节一 创设情景 【回顾】 教师活动:教师带领学生回顾前面所学知识,为下面做基础. 如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°. (1) 三边之间的关系:a2+b2=__c2___; (2) 锐角之间的关系:∠A+∠B=__90°___; (3) 边角之间的关系:sinA=_____,cosA=_____,tanA=_____. 解直角三角形的应用: (1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题); (2)根据条件的特点,适当选用锐角三角函数等知识去解直角三角形; (3)得到数学问题答案; (4)得到实际问题答案. 思考并配合老师回答问题 通过前面所学知识的复习,为后面解题做基础.
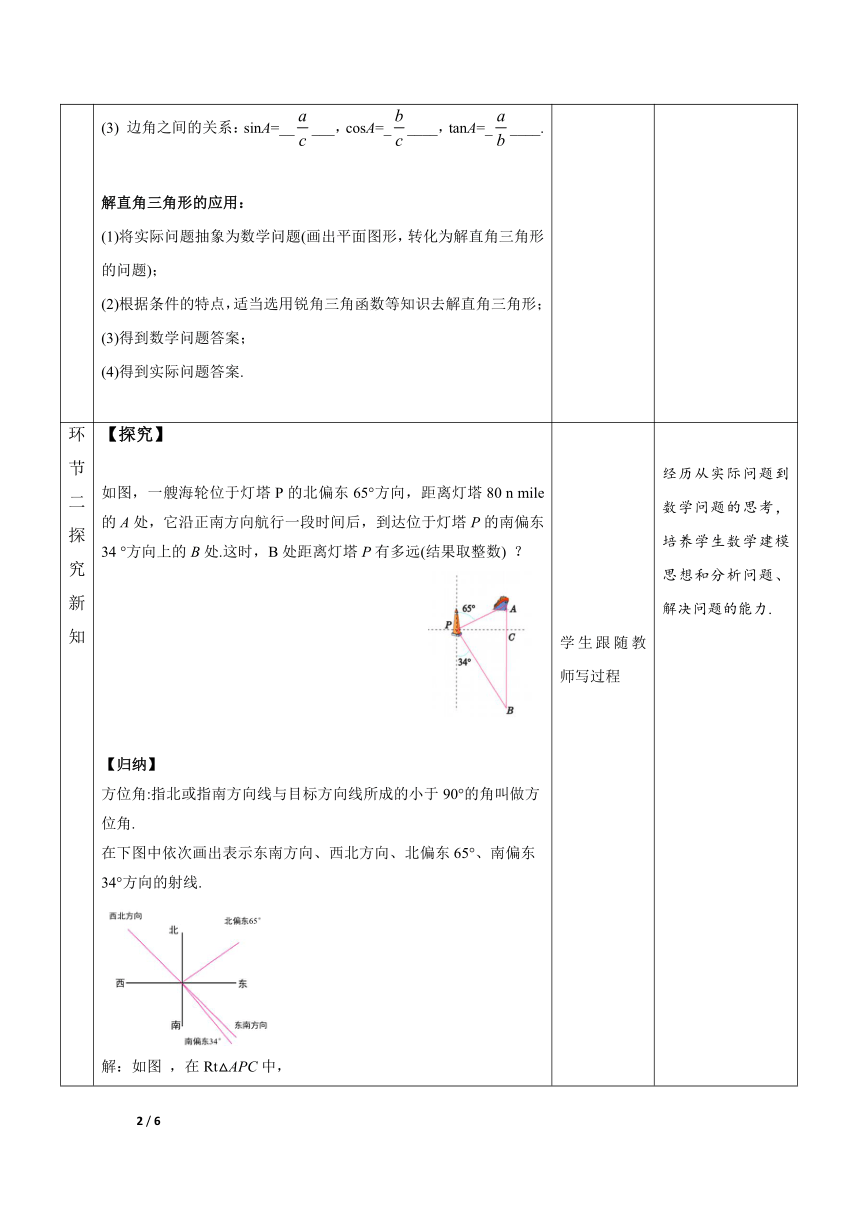
环节二探究新知 【探究】 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34 °方向上的B处.这时,B处距离灯塔P有多远(结果取整数) ? 【归纳】 方位角:指北或指南方向线与目标方向线所成的小于90°的角叫做方位角. 在下图中依次画出表示东南方向、西北方向、北偏东65°、南偏东34°方向的射线. 解:如图 ,在Rt△APC中, PC=PA·cos(90°-65°) =80×cos25° ≈72.505 在Rt△BPC中,∠B=34°, 当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130海里. 学生跟随教师写过程 经历从实际问题到数学问题的思考,培养学生数学建模思想和分析问题、解决问题的能力.
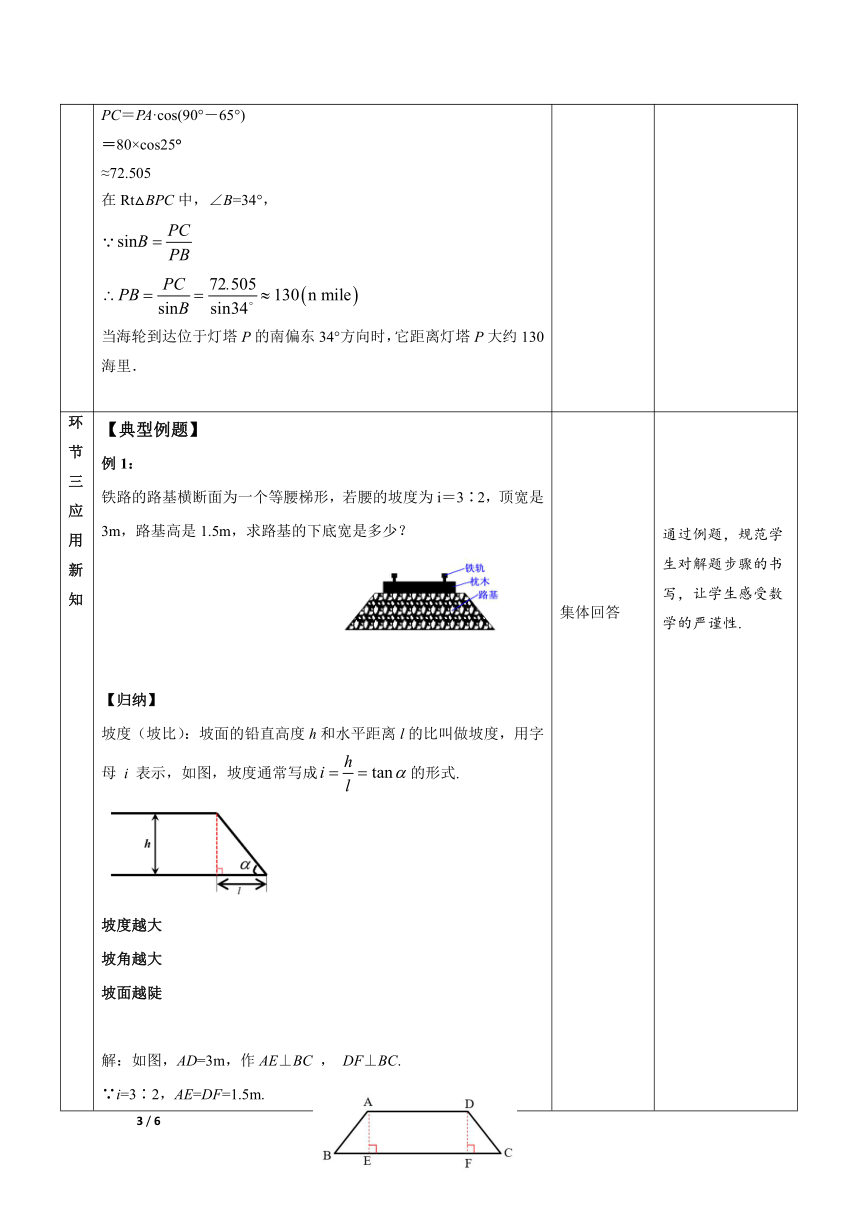
环节三应用新知 【典型例题】 例1: 铁路的路基横断面为一个等腰梯形,若腰的坡度为i=3∶2,顶宽是3m,路基高是1.5m,求路基的下底宽是多少? 【归纳】 坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母 i 表示,如图,坡度通常写成的形式. 坡度越大 坡角越大 坡面越陡 解:如图,AD=3m,作AE⊥BC , DF⊥BC. ∵i=3∶2,AE=DF=1.5m. ∴BE=CF=1m. ∴BC=1+1+3=5m. 集体回答 通过例题,规范学生对解题步骤的书写,让学生感受数学的严谨性.
环节四 巩固新知 【随堂练习】 教师活动:通过Pk作答的形式,让学生独立思考,再由老师带领整理思路过程. 练习1 如图,水库的横断面是梯形ABCD,迎水坡AB的坡度i=1∶1,坝高BE=20m,迎水坡AB=_______m,坡角α=_______. 答案:;45° 练习2 如图,海中有一个小岛A,它的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险? 答案: (方法1)解:如图,过A作AC⊥BD,交BD的延长线于点C,则AC的长是A到BD的最短距离, 由题意,得∠CAD=30°,∠CAB=60°, ∠ABD=90° - 60°= 30°, 又∵∠BAD=∠CAB-∠CAD=60° - 30°=30°, ∴∠ABD=∠BAD, ∴BD=AD=12海里, 在Rt△CAD中, ∵cos∠CAD= ∴渔船继续向正东方向行驶,没有触礁的危险. 教师活动:小组讨论,其它解题方法. (方法2)解:设AC=x海里 在Rt△ADC中,∠DAC=30° 在Rt△ABC中,∠ABC=90° - 60°= 30° ∵BC - DC=BD ∴ ∴渔船继续向正东方向行驶,没有触礁的危险. 分组讨论 进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 巩固例题练习 教科书第77页练习1、2. 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
5 / 7
28.2.2应用举例
第2课时
一、 教学目标
1.能够把解直角三角形相关知识应用到实际问题中;
2.能从实际问题中构造直角三角形,把实际问题转化为解直角三角形的问题,并能灵活选择三角函数解决问题;
3.经历从实际问题到数学问题的思考,培养学生数学建模思想和分析问题、解决问题的能力;
4.体会数学在解决实际问题中的应用,使学生感受数学在航海方面的应用,使学生感受到数学的广泛作用.
二、 教学重难点
重点:能够把解直角三角形相关知识应用到实际问题中.
难点:灵活选择三角函数解决问题.
三、教学用具
多媒体等.
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
环节一 创设情景 【回顾】 教师活动:教师带领学生回顾前面所学知识,为下面做基础. 如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°. (1) 三边之间的关系:a2+b2=__c2___; (2) 锐角之间的关系:∠A+∠B=__90°___; (3) 边角之间的关系:sinA=_____,cosA=_____,tanA=_____. 解直角三角形的应用: (1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题); (2)根据条件的特点,适当选用锐角三角函数等知识去解直角三角形; (3)得到数学问题答案; (4)得到实际问题答案. 思考并配合老师回答问题 通过前面所学知识的复习,为后面解题做基础.
环节二探究新知 【探究】 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34 °方向上的B处.这时,B处距离灯塔P有多远(结果取整数) ? 【归纳】 方位角:指北或指南方向线与目标方向线所成的小于90°的角叫做方位角. 在下图中依次画出表示东南方向、西北方向、北偏东65°、南偏东34°方向的射线. 解:如图 ,在Rt△APC中, PC=PA·cos(90°-65°) =80×cos25° ≈72.505 在Rt△BPC中,∠B=34°, 当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130海里. 学生跟随教师写过程 经历从实际问题到数学问题的思考,培养学生数学建模思想和分析问题、解决问题的能力.
环节三应用新知 【典型例题】 例1: 铁路的路基横断面为一个等腰梯形,若腰的坡度为i=3∶2,顶宽是3m,路基高是1.5m,求路基的下底宽是多少? 【归纳】 坡度(坡比):坡面的铅直高度h和水平距离l的比叫做坡度,用字母 i 表示,如图,坡度通常写成的形式. 坡度越大 坡角越大 坡面越陡 解:如图,AD=3m,作AE⊥BC , DF⊥BC. ∵i=3∶2,AE=DF=1.5m. ∴BE=CF=1m. ∴BC=1+1+3=5m. 集体回答 通过例题,规范学生对解题步骤的书写,让学生感受数学的严谨性.
环节四 巩固新知 【随堂练习】 教师活动:通过Pk作答的形式,让学生独立思考,再由老师带领整理思路过程. 练习1 如图,水库的横断面是梯形ABCD,迎水坡AB的坡度i=1∶1,坝高BE=20m,迎水坡AB=_______m,坡角α=_______. 答案:;45° 练习2 如图,海中有一个小岛A,它的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险? 答案: (方法1)解:如图,过A作AC⊥BD,交BD的延长线于点C,则AC的长是A到BD的最短距离, 由题意,得∠CAD=30°,∠CAB=60°, ∠ABD=90° - 60°= 30°, 又∵∠BAD=∠CAB-∠CAD=60° - 30°=30°, ∴∠ABD=∠BAD, ∴BD=AD=12海里, 在Rt△CAD中, ∵cos∠CAD= ∴渔船继续向正东方向行驶,没有触礁的危险. 教师活动:小组讨论,其它解题方法. (方法2)解:设AC=x海里 在Rt△ADC中,∠DAC=30° 在Rt△ABC中,∠ABC=90° - 60°= 30° ∵BC - DC=BD ∴ ∴渔船继续向正东方向行驶,没有触礁的危险. 分组讨论 进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
环节五 课堂小结 以思维导图的形式呈现本节课所讲解的内容. 回顾本节课所讲的内容 通过小结让学生进一步熟悉巩固本节课所学的知识.
环节六 布置作业 巩固例题练习 教科书第77页练习1、2. 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
5 / 7
