18.1《平行四边形的性质》 课件(共20张PPT)
文档属性
| 名称 | 18.1《平行四边形的性质》 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 14:41:40 | ||
图片预览






文档简介
(共20张PPT)
18.1.1 平行四边形的性质
人教版数学八年级下册
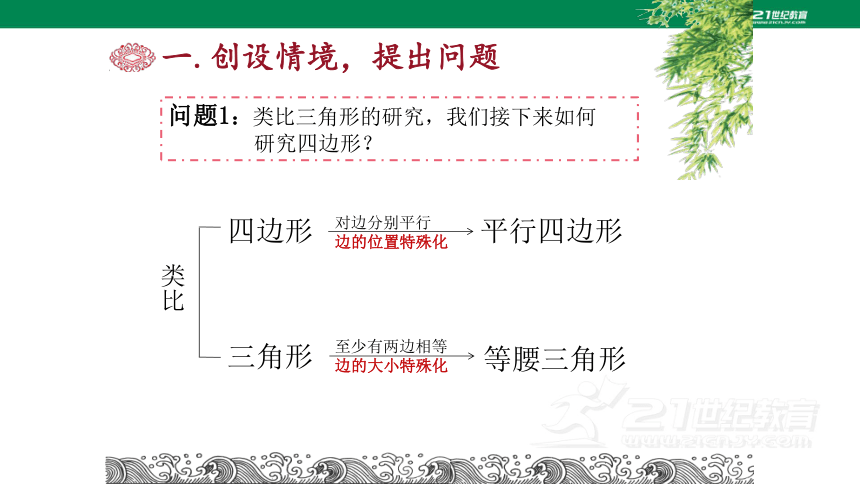
问题1:类比三角形的研究,我们接下来如何
研究四边形?
四边形
平行四边形
三角形
等腰三角形
类比
对边分别平行
边的位置特殊化
至少有两边相等
边的大小特殊化
一.创设情境,提出问题
问题2:观察以上图片,哪些实物能抽象成平行四边形呢?
二.自主探究,获取新知
平行四边形定义:
1.定义:两组对边分别平行的四边形叫做平行四边形
2.读作:平行四边形ABCD
3.记作: ABCD
A
B
C
D
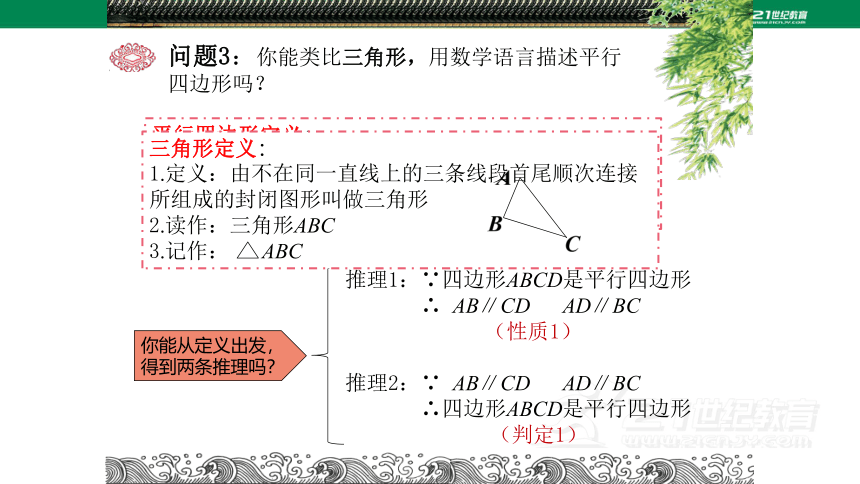
问题3:你能类比三角形,用数学语言描述平行四边形吗?
你能从定义出发,得到两条推理吗?
推理1:∵四边形ABCD是平行四边形
∴ AB∥CD AD∥BC
(性质1)
推理2:∵ AB∥CD AD∥BC
∴四边形ABCD是平行四边形
(判定1)
三角形定义:
1.定义:由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫做三角形
2.读作:三角形ABC
3.记作: ABC
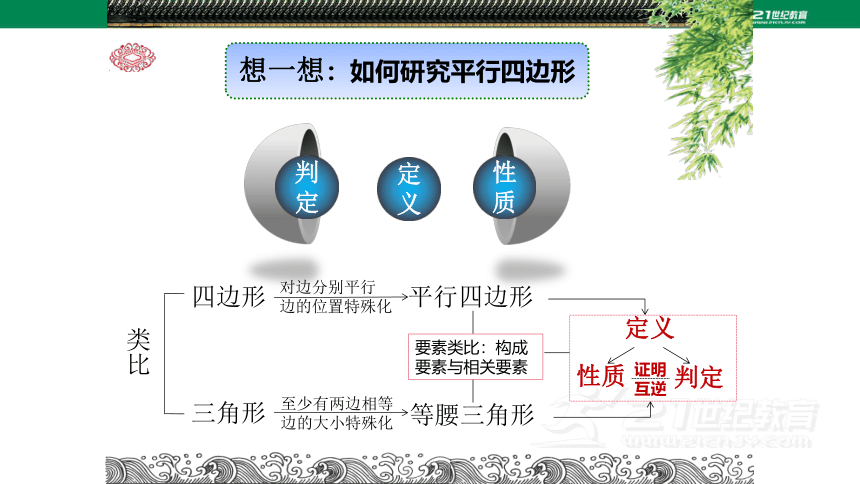
想一想:如何研究平行四边形
四边形
平行四边形
三角形
等腰三角形
类比
对边分别平行
边的位置特殊化
至少有两边相等
边的大小特殊化
定义
性质
判定
证明
互逆
要素类比:构成要素与相关要素
定义
性质
判定
问题4:平行四边形的性质可以从哪些角度考虑?
追问1:在研究等腰三角形时,我们研究了哪些要素?
追问2:回顾四边形的学习,你认为四边形有哪些要素?平行四边形中应该研究哪些要素?
根据定义画一个平行四边形,小组观察并讨论,除了“两组对边分别平行”外,它的边之间、角之间还有什么数量关系呢?度量一下,和你的猜想一致吗?
猜想1:平行四边形邻角互补.
(平行线的性质)
猜想2:平行四边形对边相等.
猜想3:平行四边形对角相等.
思考
你能证明猜想2,猜想3的正确性吗?
请用以前所学的知识和方法证明猜想2和猜想3.每组讨论后选出代表在黑板上板书.
证明:如图,连接AC.
∵ AD∥BC,AB∥CD,
∴ ∠1=∠2, ∠3=∠4.
又 AC是△ABC和△DCA的公共边.
∴ △ABC ≌△DCA.
∴AD=CB,AB=CD,
∠B=∠D.
同理,∠BAD=∠BCD.
性质1:平行四边形的对边相等:
在 ABCD中,AB=CD,AD=BC.
性质2:平行四边形的对角相等:
在 ABCD中,∠A=∠C,∠B=∠D.
请用数学语言描述平行四边形的性质.
D
A
C
B
问题4:你能根据以前所学的知识证明下列问题吗?
如图1,在: ABCD中,DE⊥AB,BF⊥CD,垂足分别为点E,F.
(1)求证:AE=CF
(2)DE=BF吗?
(3)如右图,直线a∥b,A,D为直线a上任意两点,点A到直线b的距离和点D到直线b的距离相等吗?为什么?
D
A
C
B
E
F
a
b
A
D
C
B
三.精讲点拨,解疑答惑
(1)证明:∵四边形ABCD是平行四边形
∴ ∠A= ∠C, AD=CB.
又∠AED= ∠CFB=90 °
∴ △ADE ≌ △CBF
∴AE=CF
(2)证明:∵四边形ABCD是平行四边形
∴AB=CD
又∵ AE=CF
∴AB-AE=CD-CF
∴BE=DF
(3)相等,由上可知,如果两条直线平行,那么一条直线上所有的点到另一条直线的距离相等.
根据问题4的解答,请同学们给出两条平行线间距离的概念.
两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离.
注意
两条平行线之间的任何两条平行线段都相等.如图:c=d
D
A
C
B
E
F
c
d
1.如图所示,平行四边形ABCD中,已知∠ABC=60°,则∠BAD的度数是( B )
A.60° B.120°
C.150° D.无法确定
四.巩固练习,深化新知
2.平行四边形具有而一般四边形不具有的性质是
( D )
A.内角和等于360 ° B.外角和等于360 °
C.不稳定性 D.对边平行且相等
3.在平行四边形ABCD中, ∠A:∠B:∠C:∠D的值不可能是( A )
A.1:2:3:4 B.2:2:3:3
C.2:3:2:3 D.2:3:3:2
4.如图所示,已知四边形ABCD,从(1)AB//DC;(2)AB=DC;(3)AD//BC;(4)AD=BC;(5)∠A=∠C;(6)∠B=∠D中取两个条件加以组合,能推出四边形ABCD是平行四边形的有哪几种情形?请写出具体组合.
① ⑴ ⑶ ② ⑵ ⑷ ③ ⑸ ⑹ ④ ⑴ ⑵ ⑤ ⑶ ⑷ ⑥ ⑴ ⑸ ⑦ ⑴ ⑹ ⑧ ⑶ ⑸ ⑨ ⑶ ⑹
首先谈谈本节活动的收获和体会,然后学生分组讨论并总结,代表发言,加深学生对知识的理解程度,促进学生对课堂的反思.
课堂归纳
五.归纳小结,反思提高
必做题
P43:习题1
选做题
P43:习题2
六.布置作业,分层落实
板书设计
定义:
性质证明:
性质:
02
03
04
05
01
07
06
猜想1:
猜想2:
18.1.1 平行四边形
1.定义: 两组对边分别平行的 四边形叫做平行四边形
2.性质:(1)平行四边形的对边相等
(2)平行四边形的对角相等
D
A
C
B
ABCD
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
18.1.1 平行四边形的性质
人教版数学八年级下册
问题1:类比三角形的研究,我们接下来如何
研究四边形?
四边形
平行四边形
三角形
等腰三角形
类比
对边分别平行
边的位置特殊化
至少有两边相等
边的大小特殊化
一.创设情境,提出问题
问题2:观察以上图片,哪些实物能抽象成平行四边形呢?
二.自主探究,获取新知
平行四边形定义:
1.定义:两组对边分别平行的四边形叫做平行四边形
2.读作:平行四边形ABCD
3.记作: ABCD
A
B
C
D
问题3:你能类比三角形,用数学语言描述平行四边形吗?
你能从定义出发,得到两条推理吗?
推理1:∵四边形ABCD是平行四边形
∴ AB∥CD AD∥BC
(性质1)
推理2:∵ AB∥CD AD∥BC
∴四边形ABCD是平行四边形
(判定1)
三角形定义:
1.定义:由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫做三角形
2.读作:三角形ABC
3.记作: ABC
想一想:如何研究平行四边形
四边形
平行四边形
三角形
等腰三角形
类比
对边分别平行
边的位置特殊化
至少有两边相等
边的大小特殊化
定义
性质
判定
证明
互逆
要素类比:构成要素与相关要素
定义
性质
判定
问题4:平行四边形的性质可以从哪些角度考虑?
追问1:在研究等腰三角形时,我们研究了哪些要素?
追问2:回顾四边形的学习,你认为四边形有哪些要素?平行四边形中应该研究哪些要素?
根据定义画一个平行四边形,小组观察并讨论,除了“两组对边分别平行”外,它的边之间、角之间还有什么数量关系呢?度量一下,和你的猜想一致吗?
猜想1:平行四边形邻角互补.
(平行线的性质)
猜想2:平行四边形对边相等.
猜想3:平行四边形对角相等.
思考
你能证明猜想2,猜想3的正确性吗?
请用以前所学的知识和方法证明猜想2和猜想3.每组讨论后选出代表在黑板上板书.
证明:如图,连接AC.
∵ AD∥BC,AB∥CD,
∴ ∠1=∠2, ∠3=∠4.
又 AC是△ABC和△DCA的公共边.
∴ △ABC ≌△DCA.
∴AD=CB,AB=CD,
∠B=∠D.
同理,∠BAD=∠BCD.
性质1:平行四边形的对边相等:
在 ABCD中,AB=CD,AD=BC.
性质2:平行四边形的对角相等:
在 ABCD中,∠A=∠C,∠B=∠D.
请用数学语言描述平行四边形的性质.
D
A
C
B
问题4:你能根据以前所学的知识证明下列问题吗?
如图1,在: ABCD中,DE⊥AB,BF⊥CD,垂足分别为点E,F.
(1)求证:AE=CF
(2)DE=BF吗?
(3)如右图,直线a∥b,A,D为直线a上任意两点,点A到直线b的距离和点D到直线b的距离相等吗?为什么?
D
A
C
B
E
F
a
b
A
D
C
B
三.精讲点拨,解疑答惑
(1)证明:∵四边形ABCD是平行四边形
∴ ∠A= ∠C, AD=CB.
又∠AED= ∠CFB=90 °
∴ △ADE ≌ △CBF
∴AE=CF
(2)证明:∵四边形ABCD是平行四边形
∴AB=CD
又∵ AE=CF
∴AB-AE=CD-CF
∴BE=DF
(3)相等,由上可知,如果两条直线平行,那么一条直线上所有的点到另一条直线的距离相等.
根据问题4的解答,请同学们给出两条平行线间距离的概念.
两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离.
注意
两条平行线之间的任何两条平行线段都相等.如图:c=d
D
A
C
B
E
F
c
d
1.如图所示,平行四边形ABCD中,已知∠ABC=60°,则∠BAD的度数是( B )
A.60° B.120°
C.150° D.无法确定
四.巩固练习,深化新知
2.平行四边形具有而一般四边形不具有的性质是
( D )
A.内角和等于360 ° B.外角和等于360 °
C.不稳定性 D.对边平行且相等
3.在平行四边形ABCD中, ∠A:∠B:∠C:∠D的值不可能是( A )
A.1:2:3:4 B.2:2:3:3
C.2:3:2:3 D.2:3:3:2
4.如图所示,已知四边形ABCD,从(1)AB//DC;(2)AB=DC;(3)AD//BC;(4)AD=BC;(5)∠A=∠C;(6)∠B=∠D中取两个条件加以组合,能推出四边形ABCD是平行四边形的有哪几种情形?请写出具体组合.
① ⑴ ⑶ ② ⑵ ⑷ ③ ⑸ ⑹ ④ ⑴ ⑵ ⑤ ⑶ ⑷ ⑥ ⑴ ⑸ ⑦ ⑴ ⑹ ⑧ ⑶ ⑸ ⑨ ⑶ ⑹
首先谈谈本节活动的收获和体会,然后学生分组讨论并总结,代表发言,加深学生对知识的理解程度,促进学生对课堂的反思.
课堂归纳
五.归纳小结,反思提高
必做题
P43:习题1
选做题
P43:习题2
六.布置作业,分层落实
板书设计
定义:
性质证明:
性质:
02
03
04
05
01
07
06
猜想1:
猜想2:
18.1.1 平行四边形
1.定义: 两组对边分别平行的 四边形叫做平行四边形
2.性质:(1)平行四边形的对边相等
(2)平行四边形的对角相等
D
A
C
B
ABCD
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
