广西北部湾经济区2020-2021学年九年级上学期第二次月考数学试题(含答案)
文档属性
| 名称 | 广西北部湾经济区2020-2021学年九年级上学期第二次月考数学试题(含答案) | 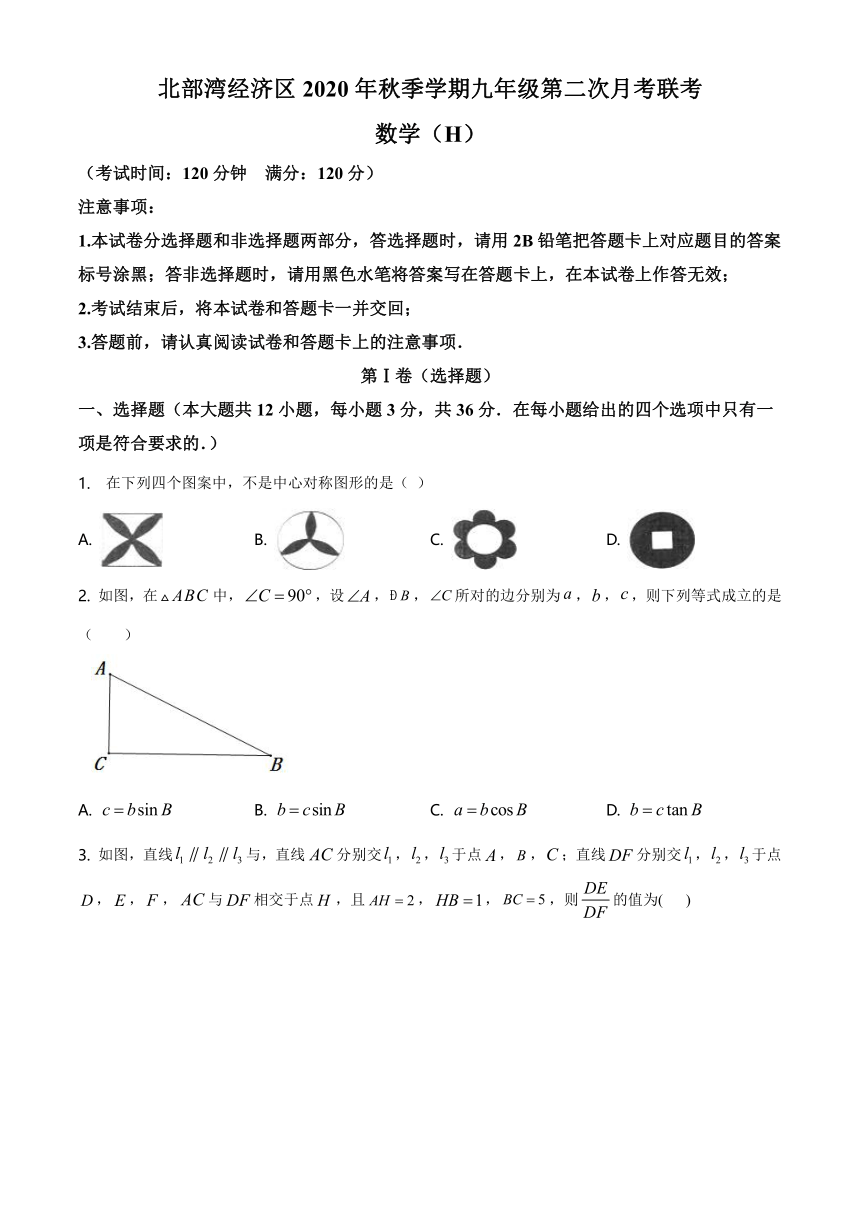 | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 14:08:23 | ||
图片预览




文档简介
北部湾经济区2020年秋季学期九年级第二次月考联考
数学(H)
(考试时间:120分钟 满分:120分)
注意事项:
1.本试卷分选择题和非选择题两部分,答选择题时,请用2B铅笔把答题卡上对应题目的答案标号涂黑;答非选择题时,请用黑色水笔将答案写在答题卡上,在本试卷上作答无效;
2.考试结束后,将本试卷和答题卡一并交回;
3.答题前,请认真阅读试卷和答题卡上的注意事项.
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的.)
1. 在下列四个图案中,不是中心对称图形的是( )
A. B. C. D.
2. 如图,在中,,设,,所对的边分别为,,,则下列等式成立的是( )
A. B. C. D.
3. 如图,直线与,直线分别交,,于点,,;直线分别交,,于点,,,与相交于点,且,,,则的值为( )
A. B. C. D.
4. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C坐标为( )
A. (2,1) B. (2,0) C. (3,3) D. (3,1)
5. 把抛物线平移得到抛物线,是怎样平移得到的( )
A. 向右平移2个单位长度,再向上平移4个单位长度
B. 向左平移2个单位长度,再向下平移4个单位长度
C. 向右平移4个单位长度,再向上平移2个单位长度
D. 向左平移4个单位长度,再向下平移2个单位长度
6. 中,、都是锐角,且,,则的形状是( ).
A. 直角三角形 B. 钝角三角形 C. 锐角三角形 D. 不能确定
7. 函数与在同一直角坐标系中图象可能是( )
A. B. C. D.
8. 如图,在平面直角坐标系中,一次函数图象与轴、轴分别相交于点,点,以线段为边作正方形,且点在反比例函数的图象上,则的值为( )
A. B. C. D. 20
9. 如图,PA、PB为圆O切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A. PA=PB B. ∠BPD=∠APD C. AB⊥PD D. AB平分PD
10. 下列命题:①两个相似多边形面积之比等于相似比的平方:②两个相似三角形的对应高之比等于它们的相似比;③在与中,,,那么;④已知及位似中心O,能够作一个且只能作一个三角形与位似,使位似比为2其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
11. 如图,在矩形中,,,以点为圆心,长为半径画弧交边于点,连接,则长为( )
A. B. C. D.
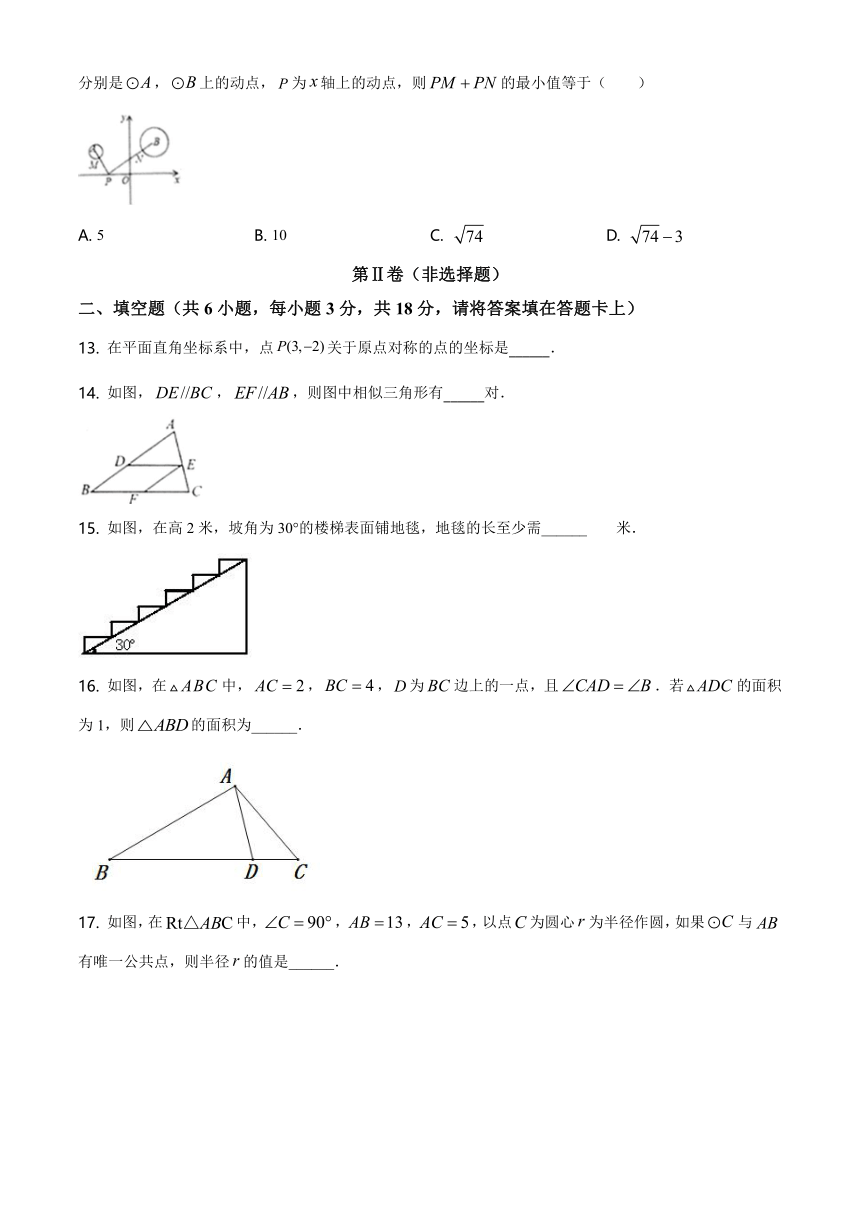
12. 如图,平面直角坐标系中,分别以点,为圆心,以1、2为半径作,,,分别是,上的动点,为轴上的动点,则的最小值等于( )
A. 5 B. 10 C. D.
第Ⅱ卷(非选择题)
二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上)
13. 在平面直角坐标系中,点关于原点对称的点的坐标是______.
14. 如图,,,则图中相似三角形有______对.
15. 如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需______米.
16. 如图,在中,,,为边上的一点,且.若的面积为1,则的面积为______.
17. 如图,在中,,,,以点为圆心为半径作圆,如果与有唯一公共点,则半径的值是______.
18. 如图,已知:函数与函数,则函数的最小值是______.
三、解答题(本大题共8小题,共66分,请将答案填在答题卡上)
19. 计算:.
20. 如图,在中,,在边上取一点,使,过作交于,.求的长.
21. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于A、B两点,已知,.
(1)求反比例函数的表达式;
(2)当时,求不等式的解集.
22. 如图,已知为的直径,是弦,且于点.连接,,.
(1)求证:;
(2)若,,求的直径.
23. 九年级数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为,向小山前进100米到达点E处,测得塔顶A的仰角为,求小山BC的高度.(结果保留根号)
24. 如图,在平行四边形中,为对角线上一点,交于点,交的延长线于点.
(1)请找出一对相似的三角形并证明;
(2)若,求的值.
25. 如图,是的直径,是的切线,切点为,交于点,点是的中点.
(1)求证:直线是的切线;
(2)若半径为1,,求图中阴影部分的面积.
26. 如图,在平面直角坐标系中,二次函数的图象与y轴交于点C,与x轴交于点A、B,点A的坐标为,点B的坐标为,且.
(1)求这个二次函数的表达式;
(2)若点是该抛物线上一点,求直线AG的表达式;
(3)点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,的面积最大?求此时点P的坐标和的最大面积.
北部湾经济区2020年秋季学期九年级第二次月考联考
数学(H)
(考试时间:120分钟 满分:120分)
注意事项:
1.本试卷分选择题和非选择题两部分,答选择题时,请用2B铅笔把答题卡上对应题目的答案标号涂黑;答非选择题时,请用黑色水笔将答案写在答题卡上,在本试卷上作答无效;
2.考试结束后,将本试卷和答题卡一并交回;
3.答题前,请认真阅读试卷和答题卡上的注意事项.
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的.)
1. 在下列四个图案中,不是中心对称图形的是( )
A. B. C. D.
【答案】B
2. 如图,在中,,设,,所对的边分别为,,,则下列等式成立的是( )
A. B. C. D.
【答案】B
3. 如图,直线与,直线分别交,,于点,,;直线分别交,,于点,,,与相交于点,且,,,则的值为( )
A. B. C. D.
【答案】C
4. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C坐标为( )
A. (2,1) B. (2,0) C. (3,3) D. (3,1)
【答案】A
5. 把抛物线平移得到抛物线,是怎样平移得到的( )
A. 向右平移2个单位长度,再向上平移4个单位长度
B. 向左平移2个单位长度,再向下平移4个单位长度
C. 向右平移4个单位长度,再向上平移2个单位长度
D. 向左平移4个单位长度,再向下平移2个单位长度
【答案】A
6. 中,、都是锐角,且,,则的形状是( ).
A. 直角三角形 B. 钝角三角形 C. 锐角三角形 D. 不能确定
【答案】C
7. 函数与在同一直角坐标系中图象可能是( )
A. B. C. D.
【答案】B
8. 如图,在平面直角坐标系中,一次函数图象与轴、轴分别相交于点,点,以线段为边作正方形,且点在反比例函数的图象上,则的值为( )
A. B. C. D. 20
【答案】A
9. 如图,PA、PB为圆O切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A. PA=PB B. ∠BPD=∠APD C. AB⊥PD D. AB平分PD
【答案】D
10. 下列命题:①两个相似多边形面积之比等于相似比的平方:②两个相似三角形的对应高之比等于它们的相似比;③在与中,,,那么;④已知及位似中心O,能够作一个且只能作一个三角形与位似,使位似比为2其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
11. 如图,在矩形中,,,以点为圆心,长为半径画弧交边于点,连接,则长为( )
A. B. C. D.
【答案】C
12. 如图,平面直角坐标系中,分别以点,为圆心,以1、2为半径作,,,分别是,上的动点,为轴上的动点,则的最小值等于( )
A. 5 B. 10 C. D.
【答案】D
第Ⅱ卷(非选择题)
二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上)
13. 在平面直角坐标系中,点关于原点对称的点的坐标是______.
【答案】
14. 如图,,,则图中相似三角形有______对.
【答案】3
15. 如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需______米.
【答案】2+2
16. 如图,在中,,,为边上的一点,且.若的面积为1,则的面积为______.
【答案】3
17. 如图,在中,,,,以点为圆心为半径作圆,如果与有唯一公共点,则半径的值是______.
【答案】
18. 如图,已知:函数与函数,则函数的最小值是______.
【答案】2
三、解答题(本大题共8小题,共66分,请将答案填在答题卡上)
19. 计算:.
【答案】
20. 如图,在中,,在边上取一点,使,过作交于,.求的长.
【答案】3
21. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于A、B两点,已知,.
(1)求反比例函数的表达式;
(2)当时,求不等式的解集.
【答案】(1);(2)或
22. 如图,已知为的直径,是弦,且于点.连接,,.
(1)求证:;
(2)若,,求的直径.
【答案】(1)证明见解析;(2).
23. 九年级数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为,向小山前进100米到达点E处,测得塔顶A的仰角为,求小山BC的高度.(结果保留根号)
【答案】米
24. 如图,在平行四边形中,为对角线上一点,交于点,交的延长线于点.
(1)请找出一对相似的三角形并证明;
(2)若,求的值.
【答案】(1),证明见解析;(2)
25. 如图,是的直径,是的切线,切点为,交于点,点是的中点.
(1)求证:直线是的切线;
(2)若半径为1,,求图中阴影部分的面积.
【答案】(1)证明见解析;(2).
26. 如图,在平面直角坐标系中,二次函数的图象与y轴交于点C,与x轴交于点A、B,点A的坐标为,点B的坐标为,且.
(1)求这个二次函数的表达式;
(2)若点是该抛物线上一点,求直线AG的表达式;
(3)点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,的面积最大?求此时点P的坐标和的最大面积.
【答案】(1);(2);(3)面积的最大值为,
数学(H)
(考试时间:120分钟 满分:120分)
注意事项:
1.本试卷分选择题和非选择题两部分,答选择题时,请用2B铅笔把答题卡上对应题目的答案标号涂黑;答非选择题时,请用黑色水笔将答案写在答题卡上,在本试卷上作答无效;
2.考试结束后,将本试卷和答题卡一并交回;
3.答题前,请认真阅读试卷和答题卡上的注意事项.
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的.)
1. 在下列四个图案中,不是中心对称图形的是( )
A. B. C. D.
2. 如图,在中,,设,,所对的边分别为,,,则下列等式成立的是( )
A. B. C. D.
3. 如图,直线与,直线分别交,,于点,,;直线分别交,,于点,,,与相交于点,且,,,则的值为( )
A. B. C. D.
4. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C坐标为( )
A. (2,1) B. (2,0) C. (3,3) D. (3,1)
5. 把抛物线平移得到抛物线,是怎样平移得到的( )
A. 向右平移2个单位长度,再向上平移4个单位长度
B. 向左平移2个单位长度,再向下平移4个单位长度
C. 向右平移4个单位长度,再向上平移2个单位长度
D. 向左平移4个单位长度,再向下平移2个单位长度
6. 中,、都是锐角,且,,则的形状是( ).
A. 直角三角形 B. 钝角三角形 C. 锐角三角形 D. 不能确定
7. 函数与在同一直角坐标系中图象可能是( )
A. B. C. D.
8. 如图,在平面直角坐标系中,一次函数图象与轴、轴分别相交于点,点,以线段为边作正方形,且点在反比例函数的图象上,则的值为( )
A. B. C. D. 20
9. 如图,PA、PB为圆O切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A. PA=PB B. ∠BPD=∠APD C. AB⊥PD D. AB平分PD
10. 下列命题:①两个相似多边形面积之比等于相似比的平方:②两个相似三角形的对应高之比等于它们的相似比;③在与中,,,那么;④已知及位似中心O,能够作一个且只能作一个三角形与位似,使位似比为2其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
11. 如图,在矩形中,,,以点为圆心,长为半径画弧交边于点,连接,则长为( )
A. B. C. D.
12. 如图,平面直角坐标系中,分别以点,为圆心,以1、2为半径作,,,分别是,上的动点,为轴上的动点,则的最小值等于( )
A. 5 B. 10 C. D.
第Ⅱ卷(非选择题)
二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上)
13. 在平面直角坐标系中,点关于原点对称的点的坐标是______.
14. 如图,,,则图中相似三角形有______对.
15. 如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需______米.
16. 如图,在中,,,为边上的一点,且.若的面积为1,则的面积为______.
17. 如图,在中,,,,以点为圆心为半径作圆,如果与有唯一公共点,则半径的值是______.
18. 如图,已知:函数与函数,则函数的最小值是______.
三、解答题(本大题共8小题,共66分,请将答案填在答题卡上)
19. 计算:.
20. 如图,在中,,在边上取一点,使,过作交于,.求的长.
21. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于A、B两点,已知,.
(1)求反比例函数的表达式;
(2)当时,求不等式的解集.
22. 如图,已知为的直径,是弦,且于点.连接,,.
(1)求证:;
(2)若,,求的直径.
23. 九年级数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为,向小山前进100米到达点E处,测得塔顶A的仰角为,求小山BC的高度.(结果保留根号)
24. 如图,在平行四边形中,为对角线上一点,交于点,交的延长线于点.
(1)请找出一对相似的三角形并证明;
(2)若,求的值.
25. 如图,是的直径,是的切线,切点为,交于点,点是的中点.
(1)求证:直线是的切线;
(2)若半径为1,,求图中阴影部分的面积.
26. 如图,在平面直角坐标系中,二次函数的图象与y轴交于点C,与x轴交于点A、B,点A的坐标为,点B的坐标为,且.
(1)求这个二次函数的表达式;
(2)若点是该抛物线上一点,求直线AG的表达式;
(3)点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,的面积最大?求此时点P的坐标和的最大面积.
北部湾经济区2020年秋季学期九年级第二次月考联考
数学(H)
(考试时间:120分钟 满分:120分)
注意事项:
1.本试卷分选择题和非选择题两部分,答选择题时,请用2B铅笔把答题卡上对应题目的答案标号涂黑;答非选择题时,请用黑色水笔将答案写在答题卡上,在本试卷上作答无效;
2.考试结束后,将本试卷和答题卡一并交回;
3.答题前,请认真阅读试卷和答题卡上的注意事项.
第Ⅰ卷(选择题)
一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合要求的.)
1. 在下列四个图案中,不是中心对称图形的是( )
A. B. C. D.
【答案】B
2. 如图,在中,,设,,所对的边分别为,,,则下列等式成立的是( )
A. B. C. D.
【答案】B
3. 如图,直线与,直线分别交,,于点,,;直线分别交,,于点,,,与相交于点,且,,,则的值为( )
A. B. C. D.
【答案】C
4. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为,在第一象限内把线段AB缩小后得到线段CD,则点C坐标为( )
A. (2,1) B. (2,0) C. (3,3) D. (3,1)
【答案】A
5. 把抛物线平移得到抛物线,是怎样平移得到的( )
A. 向右平移2个单位长度,再向上平移4个单位长度
B. 向左平移2个单位长度,再向下平移4个单位长度
C. 向右平移4个单位长度,再向上平移2个单位长度
D. 向左平移4个单位长度,再向下平移2个单位长度
【答案】A
6. 中,、都是锐角,且,,则的形状是( ).
A. 直角三角形 B. 钝角三角形 C. 锐角三角形 D. 不能确定
【答案】C
7. 函数与在同一直角坐标系中图象可能是( )
A. B. C. D.
【答案】B
8. 如图,在平面直角坐标系中,一次函数图象与轴、轴分别相交于点,点,以线段为边作正方形,且点在反比例函数的图象上,则的值为( )
A. B. C. D. 20
【答案】A
9. 如图,PA、PB为圆O切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
A. PA=PB B. ∠BPD=∠APD C. AB⊥PD D. AB平分PD
【答案】D
10. 下列命题:①两个相似多边形面积之比等于相似比的平方:②两个相似三角形的对应高之比等于它们的相似比;③在与中,,,那么;④已知及位似中心O,能够作一个且只能作一个三角形与位似,使位似比为2其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
11. 如图,在矩形中,,,以点为圆心,长为半径画弧交边于点,连接,则长为( )
A. B. C. D.
【答案】C
12. 如图,平面直角坐标系中,分别以点,为圆心,以1、2为半径作,,,分别是,上的动点,为轴上的动点,则的最小值等于( )
A. 5 B. 10 C. D.
【答案】D
第Ⅱ卷(非选择题)
二、填空题(共6小题,每小题3分,共18分,请将答案填在答题卡上)
13. 在平面直角坐标系中,点关于原点对称的点的坐标是______.
【答案】
14. 如图,,,则图中相似三角形有______对.
【答案】3
15. 如图,在高2米,坡角为30°的楼梯表面铺地毯,地毯的长至少需______米.
【答案】2+2
16. 如图,在中,,,为边上的一点,且.若的面积为1,则的面积为______.
【答案】3
17. 如图,在中,,,,以点为圆心为半径作圆,如果与有唯一公共点,则半径的值是______.
【答案】
18. 如图,已知:函数与函数,则函数的最小值是______.
【答案】2
三、解答题(本大题共8小题,共66分,请将答案填在答题卡上)
19. 计算:.
【答案】
20. 如图,在中,,在边上取一点,使,过作交于,.求的长.
【答案】3
21. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于A、B两点,已知,.
(1)求反比例函数的表达式;
(2)当时,求不等式的解集.
【答案】(1);(2)或
22. 如图,已知为的直径,是弦,且于点.连接,,.
(1)求证:;
(2)若,,求的直径.
【答案】(1)证明见解析;(2).
23. 九年级数学兴趣小组去测量一座小山的高度,在小山顶上有一高度为20米的发射塔AB,如图所示.在山脚平地上的D处测得塔底B的仰角为,向小山前进100米到达点E处,测得塔顶A的仰角为,求小山BC的高度.(结果保留根号)
【答案】米
24. 如图,在平行四边形中,为对角线上一点,交于点,交的延长线于点.
(1)请找出一对相似的三角形并证明;
(2)若,求的值.
【答案】(1),证明见解析;(2)
25. 如图,是的直径,是的切线,切点为,交于点,点是的中点.
(1)求证:直线是的切线;
(2)若半径为1,,求图中阴影部分的面积.
【答案】(1)证明见解析;(2).
26. 如图,在平面直角坐标系中,二次函数的图象与y轴交于点C,与x轴交于点A、B,点A的坐标为,点B的坐标为,且.
(1)求这个二次函数的表达式;
(2)若点是该抛物线上一点,求直线AG的表达式;
(3)点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,的面积最大?求此时点P的坐标和的最大面积.
【答案】(1);(2);(3)面积的最大值为,
同课章节目录
