冀教版数学八年级上册13.3 全等三角形的判定-第三课时 课件(共17张PPT)
文档属性
| 名称 | 冀教版数学八年级上册13.3 全等三角形的判定-第三课时 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 174.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-18 22:56:38 | ||
图片预览






文档简介
(共17张PPT)
第三课时
全等三角形的判定
1.三角形中已知三个元素,包括哪几种情况?
温故知新
答:(三个角、三个边、两边一角、两角一边)
2.到目前为止,可以作为判定两三角形全等的方法有几种?各是什么?
如图所示,小明不小心把一块三角形的玻璃打碎成四块,现在要去玻璃店配一块完全一样的玻璃,那么最省事的办法是什么?你能帮小明出出主意吗?
1
2
3
4
1.利用刻度尺、量角器、小刀等工具制作符合如下条件的三角形:
(1)△ABC,其中∠A=35°,∠B=65°,AB=5cm;
(2)△DEF,其中∠D=70°,∠E=50°,∠E的对边DF=4cm.
学 习 新 知
2.如果“两角及一边”条件中的边是两角所夹的边,那么你画的三角形与同伴画的一定完全重合吗?试试看.
有两角和夹边对应相等的两个三角形全等,简写成“ASA”或“角边角”.
3.如果“两角及一边”条件中的边是其中一角的对边,以你所画的△DEF为例,你画的三角形与同伴画的一定完全重合吗?试试看.
有两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”.
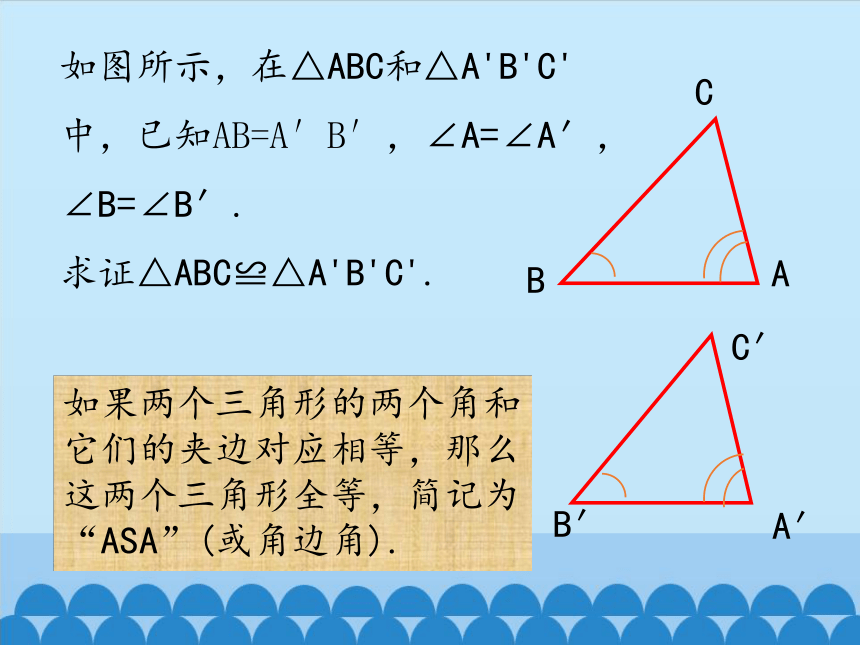
如图所示,在△ABC和△A'B'C'中,已知AB=A′B′,∠A=∠A′,∠B=∠B′.
求证△ABC≌△A'B'C'.
C′
C
A′
B
B′
A
如果两个三角形的两个角和它们的夹边对应相等,那么这两个三角形全等,简记为“ASA”(或角边角).
如图所示,已知∠ABC=∠DCB,∠A=∠D,求证:△ABC≌△DCB.
做一做
D
C
B
A
如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
“AAS”定理:
如果两个三角形的两角及其中一个角的对边对应相等,那么这两个三角形全等.简记为“AAS”(或角角边).
如何证明此定理?
已知:如图所示,AD=BE,∠A=∠FDE,BC∥EF。
求证:△ABC≌△DEF.
F
C
E
B
D
A
例题讲解
证明:∵AD=BE(已知),
∴AB=DE(等式的性质),
∵BC∥EF(已知),
∴∠ABC=∠E(两直线平行,同位角相等).
在△ABC和△DEF中,
∵
∠A=∠FDE
AB=DE,
∠ABC=∠E.
∴△ABC≌△DEF(ASA).
F
C
E
B
D
A
课堂小结
“角边角”判定三角形全等
两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
“角角边”判定三角形全等
两角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”).
检测反馈
1. 如图所示,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④∠B=∠E,∠C=∠F,AC=DE.
其中,能证明△ABC≌△DEF的条件共有 ( )
A.1组 B.2组 C.3组 D.4组
C
A
C
D
E
F
B
解析:①符合“SSS”,②符合“SAS”,③符合“ASA”,这3组都能证明△ABC≌△DEF;④不符合“AAS”,不能证明△ABC≌△DEF,故本组不正确.所以有3组条件能证明△ABC≌△DEF.故选C.
2.如图所示,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE; (2)BC=EF; (3)AC=DF;(4)∠A=∠D;(5)∠B=∠E; (6)∠C=∠F. 以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
A.(1)(5)(2) B.(1)(2)(3) C.(4)(6)(1) D.(2)(3)(4)
D
D
A
E
C
F
B
解析:A.正确,符合判定方法“SAS”;B.正确,符合判定方法“SSS”;C.正确,符合判定方法“AAS”;D.不正确,不符合全等三角形的判定方法.故选D.
3.如图所示,已知∠CAE=∠DAB,AC=AD.给出下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能判定△ABC≌△AED的条件为 .
(注:把你认为正确的答案序号都填上)
①③④
A
C
D
E
B
解析:
∵∠CAE=∠DAB,∴∠CAE+∠EAB=∠DAB+∠EAB,即∠CAB=∠DAE.又AC=AD,∴要判定△ABC≌△AED,可添加的条件为:①AB=AE(SAS);③∠C=∠D(ASA);④∠B=∠E(AAS).故填①③④.
4.如图所示,点E,C,D,A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.
求证△ABC≌△DEF.
F
C
E
B
D
A
P
证明:∵AB∥DF,
∴∠B=∠CPD,∠A=∠FDE,
∵∠E=∠CPD,∴∠E=∠B,
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
∠B=∠E,
AB=ED,
∠A=∠FDE.
解析:首先根据平行线的性质可得∠B=∠CPD,∠A=∠FDE,再由∠E=∠CPD可得∠E=∠B,再利用“ASA”证明△ABC≌△DEF.
谢 谢
第三课时
全等三角形的判定
1.三角形中已知三个元素,包括哪几种情况?
温故知新
答:(三个角、三个边、两边一角、两角一边)
2.到目前为止,可以作为判定两三角形全等的方法有几种?各是什么?
如图所示,小明不小心把一块三角形的玻璃打碎成四块,现在要去玻璃店配一块完全一样的玻璃,那么最省事的办法是什么?你能帮小明出出主意吗?
1
2
3
4
1.利用刻度尺、量角器、小刀等工具制作符合如下条件的三角形:
(1)△ABC,其中∠A=35°,∠B=65°,AB=5cm;
(2)△DEF,其中∠D=70°,∠E=50°,∠E的对边DF=4cm.
学 习 新 知
2.如果“两角及一边”条件中的边是两角所夹的边,那么你画的三角形与同伴画的一定完全重合吗?试试看.
有两角和夹边对应相等的两个三角形全等,简写成“ASA”或“角边角”.
3.如果“两角及一边”条件中的边是其中一角的对边,以你所画的△DEF为例,你画的三角形与同伴画的一定完全重合吗?试试看.
有两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”.
如图所示,在△ABC和△A'B'C'中,已知AB=A′B′,∠A=∠A′,∠B=∠B′.
求证△ABC≌△A'B'C'.
C′
C
A′
B
B′
A
如果两个三角形的两个角和它们的夹边对应相等,那么这两个三角形全等,简记为“ASA”(或角边角).
如图所示,已知∠ABC=∠DCB,∠A=∠D,求证:△ABC≌△DCB.
做一做
D
C
B
A
如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形是否一定全等?
“AAS”定理:
如果两个三角形的两角及其中一个角的对边对应相等,那么这两个三角形全等.简记为“AAS”(或角角边).
如何证明此定理?
已知:如图所示,AD=BE,∠A=∠FDE,BC∥EF。
求证:△ABC≌△DEF.
F
C
E
B
D
A
例题讲解
证明:∵AD=BE(已知),
∴AB=DE(等式的性质),
∵BC∥EF(已知),
∴∠ABC=∠E(两直线平行,同位角相等).
在△ABC和△DEF中,
∵
∠A=∠FDE
AB=DE,
∠ABC=∠E.
∴△ABC≌△DEF(ASA).
F
C
E
B
D
A
课堂小结
“角边角”判定三角形全等
两角和它们的夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
“角角边”判定三角形全等
两角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”).
检测反馈
1. 如图所示,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④∠B=∠E,∠C=∠F,AC=DE.
其中,能证明△ABC≌△DEF的条件共有 ( )
A.1组 B.2组 C.3组 D.4组
C
A
C
D
E
F
B
解析:①符合“SSS”,②符合“SAS”,③符合“ASA”,这3组都能证明△ABC≌△DEF;④不符合“AAS”,不能证明△ABC≌△DEF,故本组不正确.所以有3组条件能证明△ABC≌△DEF.故选C.
2.如图所示,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE; (2)BC=EF; (3)AC=DF;(4)∠A=∠D;(5)∠B=∠E; (6)∠C=∠F. 以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
A.(1)(5)(2) B.(1)(2)(3) C.(4)(6)(1) D.(2)(3)(4)
D
D
A
E
C
F
B
解析:A.正确,符合判定方法“SAS”;B.正确,符合判定方法“SSS”;C.正确,符合判定方法“AAS”;D.不正确,不符合全等三角形的判定方法.故选D.
3.如图所示,已知∠CAE=∠DAB,AC=AD.给出下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能判定△ABC≌△AED的条件为 .
(注:把你认为正确的答案序号都填上)
①③④
A
C
D
E
B
解析:
∵∠CAE=∠DAB,∴∠CAE+∠EAB=∠DAB+∠EAB,即∠CAB=∠DAE.又AC=AD,∴要判定△ABC≌△AED,可添加的条件为:①AB=AE(SAS);③∠C=∠D(ASA);④∠B=∠E(AAS).故填①③④.
4.如图所示,点E,C,D,A在同一条直线上,AB∥DF,ED=AB,∠E=∠CPD.
求证△ABC≌△DEF.
F
C
E
B
D
A
P
证明:∵AB∥DF,
∴∠B=∠CPD,∠A=∠FDE,
∵∠E=∠CPD,∴∠E=∠B,
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
∠B=∠E,
AB=ED,
∠A=∠FDE.
解析:首先根据平行线的性质可得∠B=∠CPD,∠A=∠FDE,再由∠E=∠CPD可得∠E=∠B,再利用“ASA”证明△ABC≌△DEF.
谢 谢
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
