6.3 一次函数的图像 课件 (共35张PPT)
文档属性
| 名称 | 6.3 一次函数的图像 课件 (共35张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 00:00:00 | ||
图片预览







文档简介
(共35张PPT)
苏科版 八年级上册数学
第6章 一次函数
6.3一次函数的图像
同学们,什么是正比例函数?
正比例函数
一般地,形如 y=kx(k 是常数,k≠0)的函数,
叫做正比例函数,其中 k 叫做比例系数.
满足两个条件:
①比例系数k是常数,且k≠0.
②两个变量x、y的次数都是1.
复习引入
问题2:描点法画函数图象的三个步骤是
_______、_______、_______.
列表
描点
连线
问题1:下列函数哪些是正比例函数?
①y=-3x ; ②y= x + 3;
③y= 4x; ④y= x2.
正比例函数有:①③
新课引入
问题.画出下列正比例函数的图象.
(1) y=2x, ; (2) y=-1.5x,y=-4x.
解: (1)函数y=2x中自变量x可为任意实数.
①列表如下:
x … 3 2 1 0 1 2 3 …
y … 6 4 2 0 2 4 6 …
合作探究
解:(1)函数y=2x中自变量x可为任意实数.
①列表如下:
x … 3 2 1 0 1 2 3 …
y … 6 4 2 0 2 4 6 …
②描点:
y=2x
y=
③连线:
同样可以画出
函数y=的图象.
观察发现:①这两个图象都是经过原点的 .
而且都经过第 象限;
一、三
直线
②变化趋势:直线从左到右 ,即y随x的增大反而 .
下降
减小
解:(2)函数y= 1.5x中自变量x可为任意实数.
①列表如下:
x … 3 2 1 0 1 2 3 …
y … 4.5 3 1.5 0 1.5 3 4.5 …
②描点:
y= 1.5x
③连线:
同样可以画出
函数y= 4x的图象.
y= 4x
①图象形状及位置:都是一条经过 和 象限的直线.
②变化趋势:直线从左到右 ,即y随x的增大反而 .
原点
第二、四
下降
减小
y= 1.5x
y=
观察发现:
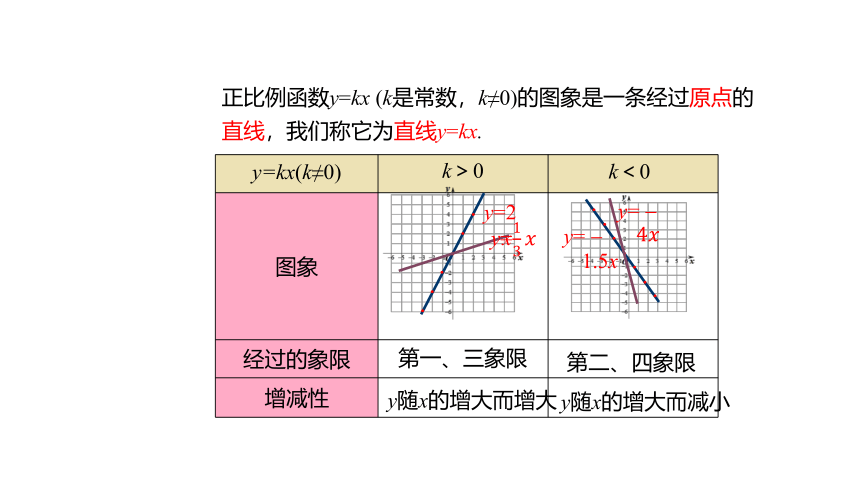
正比例函数y=kx (k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.
y=kx(k≠0)
图象
经过的象限
增减性
y= 1.5x
y=
y=2x
y=
第一、三象限
第二、四象限
y随x的增大而增大
y随x的增大而减小
k>0
k<0
正比例函数的图象是一条过原点的直线,思考下,如何确定一条直线呢?
如果是这样,我们是不是可以考虑用两点去画一条直线呢?
我知道,两点确定一条直线。
可以。
观察下面两个正比函数图象,说一说,怎样简便快速画出正比例函数图象。
y=2x,(0,0)(1,2)两点
y=1/3x,(0,0)(1,1/3)两点
由于两点确定一条直线,所以画正比例函数图象时,一般我们只需要描点(0,0)和(1,k)即可.
两点法
例1 用你认为最简单的方法画出下列函数的图象:
(1) y=-3x;(2)
O
x 0 1
y=-3x
0
-3
0
y=-3x
函数y=-3x, 的图象如下:
解:列表如下:
典例分析
例2 已知正比例函数y=(k+3)x.
解:∵函数图象经过第二、第四象限,∴k+3<0,解得k< 3.
(1)若函数图象经过第二、第四象限,则k的取值范围是________.
(2)若函数图象经过点(3,15),则k=_____.
解:将坐标(3,15)带入函数解析式中,15=(k+3)·3,解得k=2.
k< 3
2
正比例函数的图象及性质
图象:
经过原点的直线.
性质:
当k>0时,图像经过第一、三象限,y的值随着x值的增大而增大;
当k<0时,图像经过第二、四象限,y的值随着x值的增大而减小.
课堂小结
研究函数 y =kx+b(k≠0)的图象和性质:
研究方法:
画图象→观察图象→变量(坐标)意义解释.
合作探究
x -2 -1 0 1 2
y=-6x
y=-6x+5
6
0
-6
-12
12
17
11
5
-1
-7
例1:画出函数y =-6x与 y =-6x +5的图象.
解:函数y =-6x与 y =-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:
典例分析
17
11
5
-7
y=-6x
y=-6x+5
两个函数图象有什么关系?
0
x
y
x
y
0
1
5
y=-6x+5
y=-6x
不同点:
2. 函数y=6x的图象经过原点,函数
y= -6x+5的图象与y轴交于点 .
比较上面两个函数的图象的相同点与不同点.
相同点:
1. 这两个函数的图象形状都是 , 并且倾斜程度 .
联系:
3. 函数y=-6x+5可以看作由直线y=-6x向 平移 个单位长度而得到.
请大家观察这两个函数图象的形状,倾斜程度你有什么发现?
(0,5)
比较两个函数解析式,你能说出这两个函数图象有平移关系的道理吗?
y= -6x+5
y= -6x
联系:
3. 对于自变量x的任一值,这两个函数相应的y值总相差 .
相同点:
1. 这两个函数解析式都是自变量x
的 (常数)倍,与一个常数的和.
不同点:
2. 这两个函数解析式仅在 有区别.
-6
常数项
(1)所有一次函数y=kx+b的图象都是________;
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx 而得到
一条直线
互相平行
平移 个单位
其中,b叫做直线 y=kx+b在y轴上的截距.
当b>0,向上平移b个单位;
当b<0,向下平移 个单位.
合作探究
(1)直线y=2x-3可以由直线y=2x经过__________________ 而得到;
直线y=-3x+2可以由直线y=-3x经过_________________而得到;
向下平移3个单位
向上平移2个单位
(2)将直线y=-2x-1向上平移3个单位,得到的直线是 ________ .
y=-2x+2
练一练
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
例2:用两点法在同一坐标系中画出函数y=2x-1与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
用两点法画一次函数图象
典例分析
一次函数y=kx+b有下列性质:
1. 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____.
2. 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
减小
下降
增大
上升
y
x
o
2
1
·
·
·
·
y=2x+1
y=-2x+l
y=x+1
y=-x+1
观察四个函数的图像,分析在一次函数解析式y=kx+b(k,b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
画出函数y=x+1,y=-x+1,
y=2x+1,y=-2x+1的图象.
经过点(0,1),(-1,0)画出直线y=x+1;
经过点(0,1),(1,0)画出直线y=-x+1;
经过点(0,1),(-0.5,0)画出直线y=2x+1;
经过点(0,1),(0.5,0)画出直线y=-2x+1
合作探究
一次函数 y=kx+b
b 决定直线与y轴交点位置
1. 当b>0时,直线交于y正半轴
x
y
0
x
y
0
4. 当 b 相等时,直线交于y轴上同一点
2. 当b<0时,直线交于y负半轴
3. 当b = 0时,直线交于坐标原点
x
y
0
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
① b>0时,直线经过第 一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
归纳总结
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
1
2
3
4
5
x
y
正撇负捺;上加下减
1. P1(x1,y1),P2(x2,y2)是一次函数y= -0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B. y1<y2 D.当x1<x2时,y1>y2
D
根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:y越大,x就越小.
练一练
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
2. 根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
1. 一次函数y=x-2的大致图象为( )
C
A B C D
课堂练习
2. 下列哪个图象是一次函数y=-3x+5和y=2x-4的大致图象( )
(A)
(B)
(C)
(D)
B
3. 下列函数中,y的值随x值的增大而增大的函数是( )
A.y=-2x B.y=-2x+1
C.y=x-2 D.y=-x-2
C
4.已知点P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象
上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B. y1<y2 D.当x1<x2时,y1>y2
D
解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:y越大,x就越小.
5. 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
一次函数的图象和性质
图象:
一次函数y=kx+b(k,b是常数,k≠0)的图象是一条直线,
我们称它为直线y=kx+b.
画法:
①两点法:两点确定唯一一条直线;
②平移法:由直线y=kx向上或向下平移.
性质:
当k>0时:
①b>0,经过一、二、三象限,y随x的增大而增大;
②b<0,经过一、三、四象限,y随x的增大而增大;
当k<0时:
①b>0,经过一、二、四象限,y随x的增大而减小;
②b<0,经过二、三、四象限,y随x的增大而减小;
课堂小结
谢 谢!
苏科版 八年级上册数学
第6章 一次函数
6.3一次函数的图像
同学们,什么是正比例函数?
正比例函数
一般地,形如 y=kx(k 是常数,k≠0)的函数,
叫做正比例函数,其中 k 叫做比例系数.
满足两个条件:
①比例系数k是常数,且k≠0.
②两个变量x、y的次数都是1.
复习引入
问题2:描点法画函数图象的三个步骤是
_______、_______、_______.
列表
描点
连线
问题1:下列函数哪些是正比例函数?
①y=-3x ; ②y= x + 3;
③y= 4x; ④y= x2.
正比例函数有:①③
新课引入
问题.画出下列正比例函数的图象.
(1) y=2x, ; (2) y=-1.5x,y=-4x.
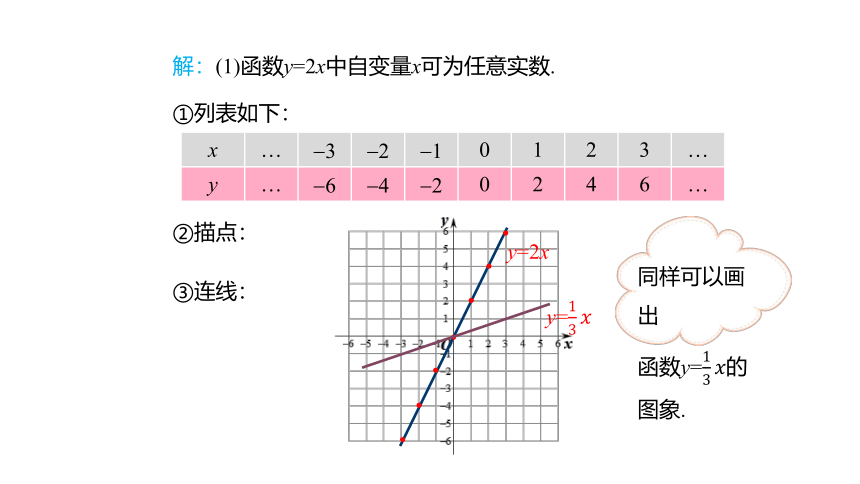
解: (1)函数y=2x中自变量x可为任意实数.
①列表如下:
x … 3 2 1 0 1 2 3 …
y … 6 4 2 0 2 4 6 …
合作探究
解:(1)函数y=2x中自变量x可为任意实数.
①列表如下:
x … 3 2 1 0 1 2 3 …
y … 6 4 2 0 2 4 6 …
②描点:
y=2x
y=
③连线:
同样可以画出
函数y=的图象.
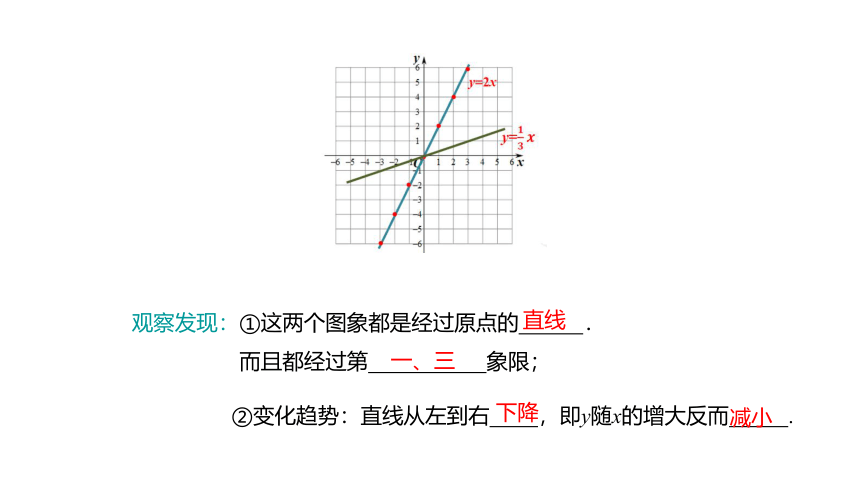
观察发现:①这两个图象都是经过原点的 .
而且都经过第 象限;
一、三
直线
②变化趋势:直线从左到右 ,即y随x的增大反而 .
下降
减小
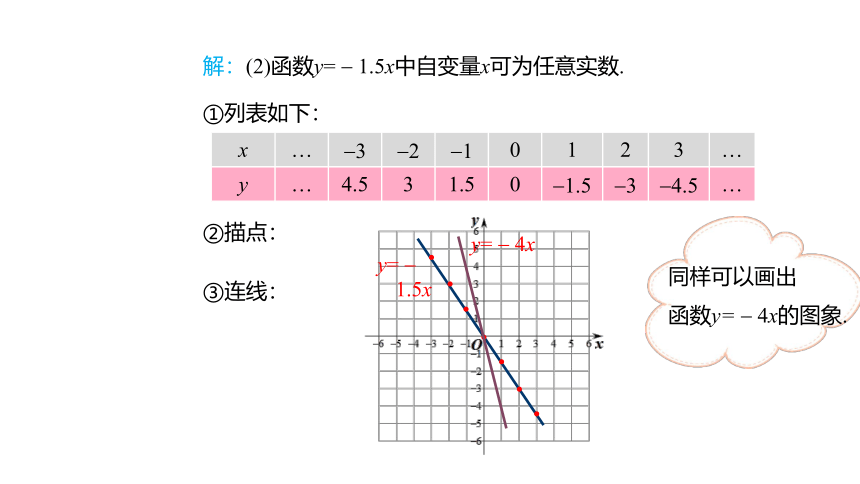
解:(2)函数y= 1.5x中自变量x可为任意实数.
①列表如下:
x … 3 2 1 0 1 2 3 …
y … 4.5 3 1.5 0 1.5 3 4.5 …
②描点:
y= 1.5x
③连线:
同样可以画出
函数y= 4x的图象.
y= 4x
①图象形状及位置:都是一条经过 和 象限的直线.
②变化趋势:直线从左到右 ,即y随x的增大反而 .
原点
第二、四
下降
减小
y= 1.5x
y=
观察发现:
正比例函数y=kx (k是常数,k≠0)的图象是一条经过原点的直线,我们称它为直线y=kx.
y=kx(k≠0)
图象
经过的象限
增减性
y= 1.5x
y=
y=2x
y=
第一、三象限
第二、四象限
y随x的增大而增大
y随x的增大而减小
k>0
k<0
正比例函数的图象是一条过原点的直线,思考下,如何确定一条直线呢?
如果是这样,我们是不是可以考虑用两点去画一条直线呢?
我知道,两点确定一条直线。
可以。
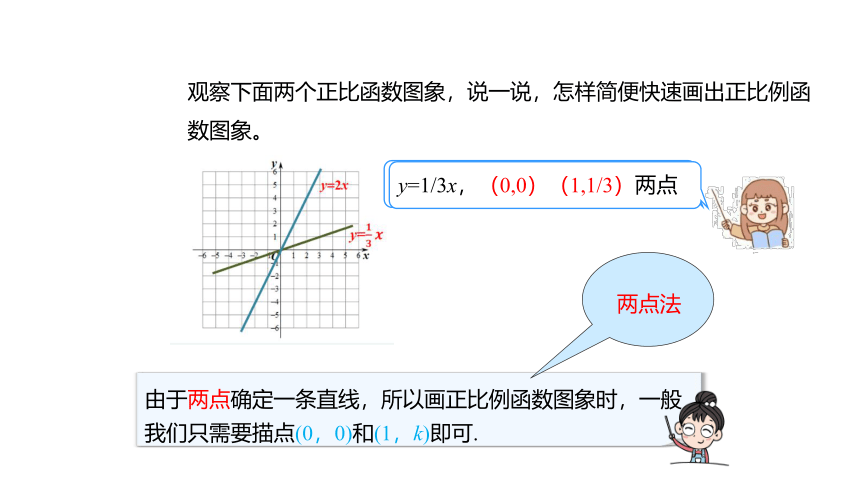
观察下面两个正比函数图象,说一说,怎样简便快速画出正比例函数图象。
y=2x,(0,0)(1,2)两点
y=1/3x,(0,0)(1,1/3)两点
由于两点确定一条直线,所以画正比例函数图象时,一般我们只需要描点(0,0)和(1,k)即可.
两点法
例1 用你认为最简单的方法画出下列函数的图象:
(1) y=-3x;(2)
O
x 0 1
y=-3x
0
-3
0
y=-3x
函数y=-3x, 的图象如下:
解:列表如下:
典例分析
例2 已知正比例函数y=(k+3)x.
解:∵函数图象经过第二、第四象限,∴k+3<0,解得k< 3.
(1)若函数图象经过第二、第四象限,则k的取值范围是________.
(2)若函数图象经过点(3,15),则k=_____.
解:将坐标(3,15)带入函数解析式中,15=(k+3)·3,解得k=2.
k< 3
2
正比例函数的图象及性质
图象:
经过原点的直线.
性质:
当k>0时,图像经过第一、三象限,y的值随着x值的增大而增大;
当k<0时,图像经过第二、四象限,y的值随着x值的增大而减小.
课堂小结
研究函数 y =kx+b(k≠0)的图象和性质:
研究方法:
画图象→观察图象→变量(坐标)意义解释.
合作探究
x -2 -1 0 1 2
y=-6x
y=-6x+5
6
0
-6
-12
12
17
11
5
-1
-7
例1:画出函数y =-6x与 y =-6x +5的图象.
解:函数y =-6x与 y =-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:
典例分析
17
11
5
-7
y=-6x
y=-6x+5
两个函数图象有什么关系?
0
x
y
x
y
0
1
5
y=-6x+5
y=-6x
不同点:
2. 函数y=6x的图象经过原点,函数
y= -6x+5的图象与y轴交于点 .
比较上面两个函数的图象的相同点与不同点.
相同点:
1. 这两个函数的图象形状都是 , 并且倾斜程度 .
联系:
3. 函数y=-6x+5可以看作由直线y=-6x向 平移 个单位长度而得到.
请大家观察这两个函数图象的形状,倾斜程度你有什么发现?
(0,5)
比较两个函数解析式,你能说出这两个函数图象有平移关系的道理吗?
y= -6x+5
y= -6x
联系:
3. 对于自变量x的任一值,这两个函数相应的y值总相差 .
相同点:
1. 这两个函数解析式都是自变量x
的 (常数)倍,与一个常数的和.
不同点:
2. 这两个函数解析式仅在 有区别.
-6
常数项
(1)所有一次函数y=kx+b的图象都是________;
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx 而得到
一条直线
互相平行
平移 个单位
其中,b叫做直线 y=kx+b在y轴上的截距.
当b>0,向上平移b个单位;
当b<0,向下平移 个单位.
合作探究
(1)直线y=2x-3可以由直线y=2x经过__________________ 而得到;
直线y=-3x+2可以由直线y=-3x经过_________________而得到;
向下平移3个单位
向上平移2个单位
(2)将直线y=-2x-1向上平移3个单位,得到的直线是 ________ .
y=-2x+2
练一练
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
例2:用两点法在同一坐标系中画出函数y=2x-1与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
用两点法画一次函数图象
典例分析
一次函数y=kx+b有下列性质:
1. 当k>0时,y随x的增大而_____ ,这时函数的图象从左到右_____.
2. 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
减小
下降
增大
上升
y
x
o
2
1
·
·
·
·
y=2x+1
y=-2x+l
y=x+1
y=-x+1
观察四个函数的图像,分析在一次函数解析式y=kx+b(k,b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
画出函数y=x+1,y=-x+1,
y=2x+1,y=-2x+1的图象.
经过点(0,1),(-1,0)画出直线y=x+1;
经过点(0,1),(1,0)画出直线y=-x+1;
经过点(0,1),(-0.5,0)画出直线y=2x+1;
经过点(0,1),(0.5,0)画出直线y=-2x+1
合作探究
一次函数 y=kx+b
b 决定直线与y轴交点位置
1. 当b>0时,直线交于y正半轴
x
y
0
x
y
0
4. 当 b 相等时,直线交于y轴上同一点
2. 当b<0时,直线交于y负半轴
3. 当b = 0时,直线交于坐标原点
x
y
0
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
① b>0时,直线经过第 一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
归纳总结
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
1
2
3
4
5
x
y
正撇负捺;上加下减
1. P1(x1,y1),P2(x2,y2)是一次函数y= -0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B. y1<y2 D.当x1<x2时,y1>y2
D
根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:y越大,x就越小.
练一练
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
2. 根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
1. 一次函数y=x-2的大致图象为( )
C
A B C D
课堂练习
2. 下列哪个图象是一次函数y=-3x+5和y=2x-4的大致图象( )
(A)
(B)
(C)
(D)
B
3. 下列函数中,y的值随x值的增大而增大的函数是( )
A.y=-2x B.y=-2x+1
C.y=x-2 D.y=-x-2
C
4.已知点P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象
上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B. y1<y2 D.当x1<x2时,y1>y2
D
解析:根据一次函数的性质: 当k<0时,y随x的增大而减小,所以D为正确答案.
提示:反过来也成立:y越大,x就越小.
5. 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
一次函数的图象和性质
图象:
一次函数y=kx+b(k,b是常数,k≠0)的图象是一条直线,
我们称它为直线y=kx+b.
画法:
①两点法:两点确定唯一一条直线;
②平移法:由直线y=kx向上或向下平移.
性质:
当k>0时:
①b>0,经过一、二、三象限,y随x的增大而增大;
②b<0,经过一、三、四象限,y随x的增大而增大;
当k<0时:
①b>0,经过一、二、四象限,y随x的增大而减小;
②b<0,经过二、三、四象限,y随x的增大而减小;
课堂小结
谢 谢!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
