人教A版(2019)高中数学选择性必修第一册 《圆的一般方程》名师课件(共29张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 《圆的一般方程》名师课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
圆心为,半径为的圆的标准方程是什么
复习引入
直线方程有多种形式,圆的方程是否还可以表示成其他形式 这是一个需要探讨的问题.
复习引入
人教A版同步教材名师课件
圆的一般方程
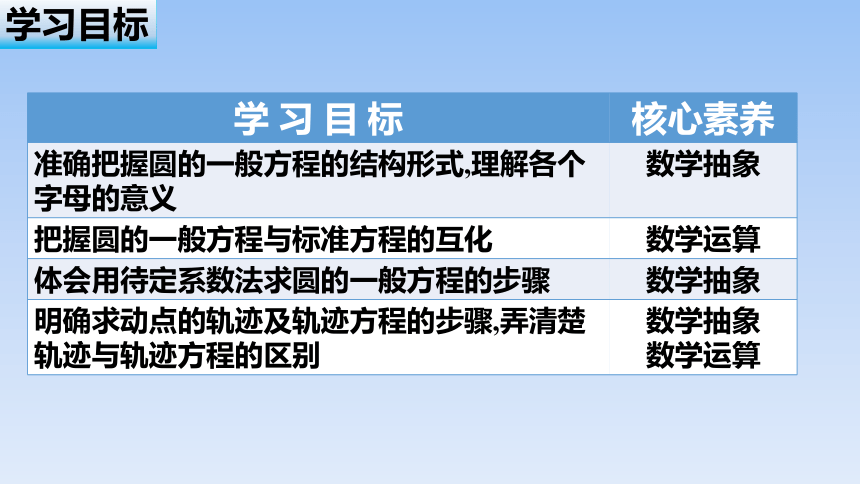
学习目标
学 习 目 标 核心素养
准确把握圆的一般方程的结构形式,理解各个字母的意义 数学抽象
把握圆的一般方程与标准方程的互化 数学运算
体会用待定系数法求圆的一般方程的步骤 数学抽象
明确求动点的轨迹及轨迹方程的步骤,弄清楚轨迹与轨迹方程的区别 数学抽象
数学运算
学习目标
学习目标:
1.正确理解圆的方程的形式及特点,会由一般式求圆心和半径.
2.会在不同条件下求圆的一般方程.
学科核心素养:
1. 通过圆的一般方程的推导,提升逻辑推理、数学运算的数学素养.
2. 通过学习圆的一般方程的应用,培养数学运算的数学素养.
思考1:圆的标准方程展开可得到一个什么式子
思考2:方程的一般形式是什么
探究新知
思考3:方程与表示的图形都是圆吗 为什么
思考4:方程可化为 ,它在什么条件下表示圆
探究新知
思考5:当或 时,方程表示什么图形
思考6:方程 叫做圆的一般方程,其圆心坐标和半径分别是什么
圆心为,半径为
探究新知
圆的一般方程
探究新知
特点:①和的系数相同都等于1;
②没有这样的二次项.
我们把方程
称为圆的一般方程
思考7:当或时,圆的位置分别有什么特点
C
o
C
o
C
o
探究新知
圆的标准方程 圆的一般方程
方程形式
圆心
半径
优点
几何特征明显
突出方程形式上的特点
探究新知
例1、判断方程能否表示圆,若能表示圆,求出圆心和半径.
典例讲解
法一:由方程可知,
所以,
所以当时,它表示一个点;当时,它表示圆的方程,
此时,圆的圆心为,半径为
法二:原方程可化为,
所以当时,它表示一个点;当时,它表示圆的方程,
此时,圆的圆心为,半径为
解析
任何一个圆的方程都可化为的形式,但形如的方程不一定表示圆.判断它是否表示圆可以有以下两种方法:
(1)计算,若其值为正,则表示圆;若其值为0,则表示一个点;若其值为负,则不表示任何图形.
方法归纳
(2)将该方程配方为,根据圆的标
准方程来判断.
典例讲解
法一:设所求的圆的方程为x2+y2+Dx+Ey+F=0,
因为,,在圆上,所以它们的坐标是方程的解,
代入方程可得
所求圆的方程为x2+y2-8x+6y=0,圆的半径,圆心坐标是(4,-3).
例2、求过三点、 、 圆的方程,并求这个圆的半径和圆心坐标.
解析
待定系数法
典例讲解
例2、求过三点、 、 圆的方程,并求这个圆的半径和圆心坐标.
解析
法二:设所求圆的方程为:
因为、 、 都在圆上
所以
所求圆的方程为.
圆的半径,圆心坐标是(4,-3).
法三:先求出圆心和半径,再求圆的方程
O
M1
M2
C
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点的距离
几何法
典例讲解
例2、求过三点、 、 圆的方程,并求这个圆的半径和圆心坐标.
求圆的方程
几何方法
求圆心坐标 (两条直线的交点)(常用弦的中垂线)
求半径(圆心到圆上一点的距离)
写出圆的标准方程
待定系数法
列关于(或)的方程组
解出(或)写出标准方程(或一般方程)
方法归纳
设方程为
1、已知A(2,2),B(5,3),C(3, 1),求三角形ABC的外接圆的方程.
变式训练
设三角形外接圆的方程为x2+y2+Dx+Ey+F=0,
由题意得
即三角形的外接圆方程为.
解析
相关点法
典例讲解
例 、已知线段上运动,求线段 的中点 的轨迹方程.
解析
设点的坐标是,点的坐标是由于点坐标是,且点是线段的中点,所以
因为点在圆上运动,所以点坐标满足方程,即
把(1)代入(2)得
整理得即为所求的轨迹方程.
(1)求轨迹方程的三种常用方法
①直接法:根据题目条件,建立坐标系,设出动点坐标,找出动点满足的条件,然后化简、证明.
②定义法:动点的运动轨迹符合圆的定义时,可利用定义写出动点的轨迹方程.
③代入法:若动点P(x,y)依赖于某圆上的一个动点Q(x1,y1)而运动,把x1,y1用x,y表示,再将Q点的坐标代入到已知圆的方程中得P点的轨迹方程.
(2)①求出轨迹方程后应说出最后是什么样的图形;②要考虑轨迹上应去掉的点及轨迹不存在的情形.
方法归纳
变式训练
解析
2、已知线段上运动,求线段 的轨迹方程.
设点的坐标是,点的坐标是.
由于点坐标是,且点是线段的中点,所以
因为点在圆上运动,所以点坐标满足方程,即
把(1)代入(2)得
整理得即为所求的轨迹方程.
素养提炼
1.圆的一般方程的特点
圆的一般方程x2+y2+Dx+Ey+F=0(其中为常数)具有以下特点:
(1) x2,y2的项的系数均为1.
(2)没有xy项.
(3)
素养提炼
2.求圆的方程的基本思路
(1)求圆的方程时,若已知条件中明确圆心的坐标或半径,则设圆的标准方程求解;若已知条件中没有明确圆心坐标或半径大小设圆的一般方程求解.
(2)由于圆的一般方程中所含的三个特定系数不是二次项的系数,在由三个独立条件列出方程组后,一般可求出待定系数.
(3)若求圆心和半径,则可以将圆的一般方程配方成圆的标准方程,再写出圆心坐标和半径.另外在解答圆的有关问题时,应注意利用圆的平面几何的性质,使运算简化.
素养提炼
3.求轨迹方程的一般步骤
(1)建系:建立适当的直角坐标系.
(2)设点:用(x,y)表示轨迹(曲线)上任意一点的坐标.
(3)列式:列出关于x,y的方程.
(4)化简:把方程化为最简形式.
(5)证明:证明以化简后的方程的解为坐标的点都是曲线上的点.
当堂练习
方程,可化为,即,∴方程表示点.
1.方程表示的图形是( )
A.一个点 B.一个圆 C.一条直线 D.不存在
解析
A
2.若方程表示一个圆,则实数的取值范围是( )
由得解得故选A.
解析
A
当堂练习
由条件可知,直线经过圆的圆心,∴ ,解得.
3.若圆关于直线
对称,则实数等于______.
解析
由条件知, 设,则,由于在圆上,
∴整理得.
4.设圆的圆心为,点在圆上,则的中心的轨迹方程是__________________________.
解析
当堂练习
设所求圆的方程为x2+y2+Dx+Ey+F=0(D2+E2 -4F>0),
由题意可得解得
故所求外接圆的方程为.
5.已知的三个顶点分别为, ,,求其外接圆P的方程.
解析
2.用待定系数法求圆方程的基本步骤:
(1)设圆方程 ;
(2)列方程组;
(3)求系数;
(4)写出圆方程.
3.相关点法求轨迹方程
1.圆的一般方程:
归纳小结
P88 习题 2.4: 3、4
作 业
圆心为,半径为的圆的标准方程是什么
复习引入
直线方程有多种形式,圆的方程是否还可以表示成其他形式 这是一个需要探讨的问题.
复习引入
人教A版同步教材名师课件
圆的一般方程
学习目标
学 习 目 标 核心素养
准确把握圆的一般方程的结构形式,理解各个字母的意义 数学抽象
把握圆的一般方程与标准方程的互化 数学运算
体会用待定系数法求圆的一般方程的步骤 数学抽象
明确求动点的轨迹及轨迹方程的步骤,弄清楚轨迹与轨迹方程的区别 数学抽象
数学运算
学习目标
学习目标:
1.正确理解圆的方程的形式及特点,会由一般式求圆心和半径.
2.会在不同条件下求圆的一般方程.
学科核心素养:
1. 通过圆的一般方程的推导,提升逻辑推理、数学运算的数学素养.
2. 通过学习圆的一般方程的应用,培养数学运算的数学素养.
思考1:圆的标准方程展开可得到一个什么式子
思考2:方程的一般形式是什么
探究新知
思考3:方程与表示的图形都是圆吗 为什么
思考4:方程可化为 ,它在什么条件下表示圆
探究新知
思考5:当或 时,方程表示什么图形
思考6:方程 叫做圆的一般方程,其圆心坐标和半径分别是什么
圆心为,半径为
探究新知
圆的一般方程
探究新知
特点:①和的系数相同都等于1;
②没有这样的二次项.
我们把方程
称为圆的一般方程
思考7:当或时,圆的位置分别有什么特点
C
o
C
o
C
o
探究新知
圆的标准方程 圆的一般方程
方程形式
圆心
半径
优点
几何特征明显
突出方程形式上的特点
探究新知
例1、判断方程能否表示圆,若能表示圆,求出圆心和半径.
典例讲解
法一:由方程可知,
所以,
所以当时,它表示一个点;当时,它表示圆的方程,
此时,圆的圆心为,半径为
法二:原方程可化为,
所以当时,它表示一个点;当时,它表示圆的方程,
此时,圆的圆心为,半径为
解析
任何一个圆的方程都可化为的形式,但形如的方程不一定表示圆.判断它是否表示圆可以有以下两种方法:
(1)计算,若其值为正,则表示圆;若其值为0,则表示一个点;若其值为负,则不表示任何图形.
方法归纳
(2)将该方程配方为,根据圆的标
准方程来判断.
典例讲解
法一:设所求的圆的方程为x2+y2+Dx+Ey+F=0,
因为,,在圆上,所以它们的坐标是方程的解,
代入方程可得
所求圆的方程为x2+y2-8x+6y=0,圆的半径,圆心坐标是(4,-3).
例2、求过三点、 、 圆的方程,并求这个圆的半径和圆心坐标.
解析
待定系数法
典例讲解
例2、求过三点、 、 圆的方程,并求这个圆的半径和圆心坐标.
解析
法二:设所求圆的方程为:
因为、 、 都在圆上
所以
所求圆的方程为.
圆的半径,圆心坐标是(4,-3).
法三:先求出圆心和半径,再求圆的方程
O
M1
M2
C
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点的距离
几何法
典例讲解
例2、求过三点、 、 圆的方程,并求这个圆的半径和圆心坐标.
求圆的方程
几何方法
求圆心坐标 (两条直线的交点)(常用弦的中垂线)
求半径(圆心到圆上一点的距离)
写出圆的标准方程
待定系数法
列关于(或)的方程组
解出(或)写出标准方程(或一般方程)
方法归纳
设方程为
1、已知A(2,2),B(5,3),C(3, 1),求三角形ABC的外接圆的方程.
变式训练
设三角形外接圆的方程为x2+y2+Dx+Ey+F=0,
由题意得
即三角形的外接圆方程为.
解析
相关点法
典例讲解
例 、已知线段上运动,求线段 的中点 的轨迹方程.
解析
设点的坐标是,点的坐标是由于点坐标是,且点是线段的中点,所以
因为点在圆上运动,所以点坐标满足方程,即
把(1)代入(2)得
整理得即为所求的轨迹方程.
(1)求轨迹方程的三种常用方法
①直接法:根据题目条件,建立坐标系,设出动点坐标,找出动点满足的条件,然后化简、证明.
②定义法:动点的运动轨迹符合圆的定义时,可利用定义写出动点的轨迹方程.
③代入法:若动点P(x,y)依赖于某圆上的一个动点Q(x1,y1)而运动,把x1,y1用x,y表示,再将Q点的坐标代入到已知圆的方程中得P点的轨迹方程.
(2)①求出轨迹方程后应说出最后是什么样的图形;②要考虑轨迹上应去掉的点及轨迹不存在的情形.
方法归纳
变式训练
解析
2、已知线段上运动,求线段 的轨迹方程.
设点的坐标是,点的坐标是.
由于点坐标是,且点是线段的中点,所以
因为点在圆上运动,所以点坐标满足方程,即
把(1)代入(2)得
整理得即为所求的轨迹方程.
素养提炼
1.圆的一般方程的特点
圆的一般方程x2+y2+Dx+Ey+F=0(其中为常数)具有以下特点:
(1) x2,y2的项的系数均为1.
(2)没有xy项.
(3)
素养提炼
2.求圆的方程的基本思路
(1)求圆的方程时,若已知条件中明确圆心的坐标或半径,则设圆的标准方程求解;若已知条件中没有明确圆心坐标或半径大小设圆的一般方程求解.
(2)由于圆的一般方程中所含的三个特定系数不是二次项的系数,在由三个独立条件列出方程组后,一般可求出待定系数.
(3)若求圆心和半径,则可以将圆的一般方程配方成圆的标准方程,再写出圆心坐标和半径.另外在解答圆的有关问题时,应注意利用圆的平面几何的性质,使运算简化.
素养提炼
3.求轨迹方程的一般步骤
(1)建系:建立适当的直角坐标系.
(2)设点:用(x,y)表示轨迹(曲线)上任意一点的坐标.
(3)列式:列出关于x,y的方程.
(4)化简:把方程化为最简形式.
(5)证明:证明以化简后的方程的解为坐标的点都是曲线上的点.
当堂练习
方程,可化为,即,∴方程表示点.
1.方程表示的图形是( )
A.一个点 B.一个圆 C.一条直线 D.不存在
解析
A
2.若方程表示一个圆,则实数的取值范围是( )
由得解得故选A.
解析
A
当堂练习
由条件可知,直线经过圆的圆心,∴ ,解得.
3.若圆关于直线
对称,则实数等于______.
解析
由条件知, 设,则,由于在圆上,
∴整理得.
4.设圆的圆心为,点在圆上,则的中心的轨迹方程是__________________________.
解析
当堂练习
设所求圆的方程为x2+y2+Dx+Ey+F=0(D2+E2 -4F>0),
由题意可得解得
故所求外接圆的方程为.
5.已知的三个顶点分别为, ,,求其外接圆P的方程.
解析
2.用待定系数法求圆方程的基本步骤:
(1)设圆方程 ;
(2)列方程组;
(3)求系数;
(4)写出圆方程.
3.相关点法求轨迹方程
1.圆的一般方程:
归纳小结
P88 习题 2.4: 3、4
作 业
