北师大版数学六年级上册 第1单元 圆-练习一课件(共36张PPT)
文档属性
| 名称 | 北师大版数学六年级上册 第1单元 圆-练习一课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 11:18:14 | ||
图片预览











文档简介
(共36张PPT)
练习一
第1单元·圆
CONTENTS
目录
练 习 一
03
牛刀小试
02
知识梳理
01
课堂小结
知识梳理
练 习 一
知识点/01 圆的认识(一)
圆是由一条曲线围成的封闭图形,圆上任意一点到圆的中心的距离都相等。
a.
练 习 一
知识点/01 圆的认识(一)
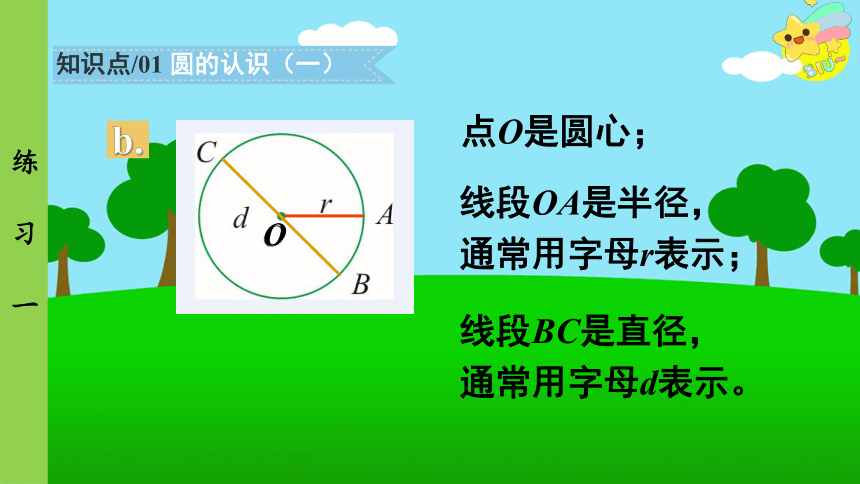
b.
点O是圆心;
线段OA是半径,
通常用字母r表示;
线段BC是直径,通常用字母d表示。
O
练 习 一
知识点/01 圆的认识(一)
c.
在同圆或等圆内,所有的半径都相等,所有的直径也都相等,直径的长度是半径的2倍,半径的长度是直径的一半。圆心确定圆的位置,半径确定圆的大小。
练 习 一
知识点/02 圆的认识(二)
在圆形纸片上折叠的折痕都通过了圆心,每一条直径所在的直线都是圆的对称轴。圆有无数条对称轴。
a.
b.
等腰三角形和等腰梯形都有1条对称轴,长方形有2条对称轴,等边三角形有3条对称轴,正方形有4条对称轴,圆有无数条对称轴。
练 习 一
知识点/02 圆的认识(二)
找圆心的方法:(1)把圆对折后再对折,两条半径的公共端点就是圆心;(2)把圆沿直径所在的直线任意对折两次,折痕的交点就是圆心。
c.
d.
圆与正多边形的组合图形的对称轴的条数取决于正多边形的对称轴的条数。
练 习 一
知识点/03 欣赏与设计
圆在图案设计中有广泛应用,基本图形经过变换后,可以构成不同的美丽图案。
a.
b.
圆在图案设计中有广泛应用,设计时可单独或综合运用平移、轴对称等知识。
练 习 一
知识点/04 圆的周长
对于较小的圆可以用滚动法和绕线法测量出圆的周长。
a.
b.
圆的周长与直径有关。任意一个圆的周长除以直径的商都是一个固定的数,我们把它叫作圆周率,用字母π表示,计算时通常取3.14。
练 习 一
知识点/04 圆的周长
用C表示圆的周长,则C=πd或C=2πr。用圆的周长计算公式可以解答一些简单的实际问题。
c.
d.
生活中可以运用圆的周长公式C=πd或C=2πr解决求圆形物体的周长或直径、半径的问题。
练 习 一
知识点/05 圆周率的历史
古希腊的阿基米德和我国古代的刘徽想到的计算圆周率的方法在本质上是一致的,都是把圆的周长转化成正多边形的周长。
练 习 一
知识点/06 圆的面积(一)
圆的面积=圆的周长的一半×半径,如果用S表示圆的面积,r表示圆的半径,那么圆的面积计算公式是S=πr2。
练 习 一
知识点/06 圆的面积(二)
a.
已知圆的半径求圆的面积,直接用公式S=πr2计算即可。若已知圆的直径求圆的面积,则要先用“r=d÷2”求出半径后再计算,或直接用公式S=π(d÷2)2计算。
练 习 一
知识点/06 圆的面积(二)
b.
已知圆的周长求圆的面积,应先利用周长公式C=2πr求出半径,再利用圆的面积公式计算。综合算式为S=π (C÷2π) 2。
c.
圆的面积可以通过把圆形转化成三角形推导出来,圆的面积:S=πr2。
牛刀小试
练 习 一
1.
(1)你能在左面的正方形中画一个面积最大的圆吗?
(2)剪去最大的圆,剩下部分的面积是多少?
4cm
4×4 - 3.14×(4÷2)2
=16 - 3.14×4
=3.44(cm2)
练 习 一
2.填一填。
半径/cm
直径/cm
周长/cm
面积/cm2
0.5
1
9.42
14
3.14
0.785
7.065
153.86
43.96
3
1.5
7
练 习 一
3.
3.14×62=113.04(m2)
练 习 一
4. 某钟表的分针长10cm。
3.14×(10×2)=62.8(厘米)
(1)从1时到2时,分针针尖走过了多少厘米?
3.14×102=314(平方厘米)
(2)从1时到2时,分针扫过的面积是多少平方厘米?
练 习 一
5.要为一个水缸做一个盖子,这个盖子的面积至少是多少平方米?
3.14×(1÷2) 2=0.785(平方米)
答:这个盖子的面积至少是0.785平方米。
练 习 一
6.
12.56÷10÷3.14=0.4(m)
练 习 一
7.常见的自行车车轮的直径如下表。
3.14×559=1755.26(mm)
3.14×610=1915.4(mm)
3.14×660=2072.4(mm)
3.14×711=2232.54(mm)
每种自行车车轮滚动1圈经过的距离分别是多少?
练 习 一
8.长方形的宽是多少厘米?
3.14×(16÷2) 2÷16=12.56(厘米)
练 习 一
9.淘气用两根长度都是62.8cm的铁丝分别围成正方形和圆,它们围成的面积一样大吗?
正方形:62.8÷4=15.7(cm)
15.7×15.7=246.49(cm2)
圆:62.8÷3.14÷2=10(cm)
3.14×102=314(cm2)
因为314>246.49,所以圆的面积大。
练 习 一
10.某汽车车轮的直径为0.5m,汽车行驶到1km时,车轮大约转了多少圈?(结果保留整数)
3.14×0.5=1.57(m)
1km=1000m
1000÷1.57≈637(圈)
答:车轮大约转了637圈。
练 习 一
11.起跑线。
(1)想一想,填一填。
笑笑和淘气分别从A,B处出发,沿半圆走到C,D。他们两人走过的路程一样长吗?
不一样长。
练 习 一
①笑笑所走路线的半径为10m,她走过的路程是 m。
②淘气所走路线的半径为 m,他走过的路程是 m。
③两人走过的路程相差 m。
31.4
3.14
34.54
11
练 习 一
(2)小调查。
在400m比赛中,运动员所在的起跑线位置是不一样的,你知道这是为什么吗?
练 习 一
因为往外一圈的弯道比里面的弯道长,所以运动员的起跑位置会依次向前移相应的距离。调查略。
练 习 一
练 习 一
课堂小结
练 习 一
通过这节课的学习活动,
你有什么收获?
练 习 一
课后作业
2.完成练习册本课时的习题。
1.从课后习题中选取;
谢 谢 观 看
Thanks to watching
练习一
第1单元·圆
CONTENTS
目录
练 习 一
03
牛刀小试
02
知识梳理
01
课堂小结
知识梳理
练 习 一
知识点/01 圆的认识(一)
圆是由一条曲线围成的封闭图形,圆上任意一点到圆的中心的距离都相等。
a.
练 习 一
知识点/01 圆的认识(一)
b.
点O是圆心;
线段OA是半径,
通常用字母r表示;
线段BC是直径,通常用字母d表示。
O
练 习 一
知识点/01 圆的认识(一)
c.
在同圆或等圆内,所有的半径都相等,所有的直径也都相等,直径的长度是半径的2倍,半径的长度是直径的一半。圆心确定圆的位置,半径确定圆的大小。
练 习 一
知识点/02 圆的认识(二)
在圆形纸片上折叠的折痕都通过了圆心,每一条直径所在的直线都是圆的对称轴。圆有无数条对称轴。
a.
b.
等腰三角形和等腰梯形都有1条对称轴,长方形有2条对称轴,等边三角形有3条对称轴,正方形有4条对称轴,圆有无数条对称轴。
练 习 一
知识点/02 圆的认识(二)
找圆心的方法:(1)把圆对折后再对折,两条半径的公共端点就是圆心;(2)把圆沿直径所在的直线任意对折两次,折痕的交点就是圆心。
c.
d.
圆与正多边形的组合图形的对称轴的条数取决于正多边形的对称轴的条数。
练 习 一
知识点/03 欣赏与设计
圆在图案设计中有广泛应用,基本图形经过变换后,可以构成不同的美丽图案。
a.
b.
圆在图案设计中有广泛应用,设计时可单独或综合运用平移、轴对称等知识。
练 习 一
知识点/04 圆的周长
对于较小的圆可以用滚动法和绕线法测量出圆的周长。
a.
b.
圆的周长与直径有关。任意一个圆的周长除以直径的商都是一个固定的数,我们把它叫作圆周率,用字母π表示,计算时通常取3.14。
练 习 一
知识点/04 圆的周长
用C表示圆的周长,则C=πd或C=2πr。用圆的周长计算公式可以解答一些简单的实际问题。
c.
d.
生活中可以运用圆的周长公式C=πd或C=2πr解决求圆形物体的周长或直径、半径的问题。
练 习 一
知识点/05 圆周率的历史
古希腊的阿基米德和我国古代的刘徽想到的计算圆周率的方法在本质上是一致的,都是把圆的周长转化成正多边形的周长。
练 习 一
知识点/06 圆的面积(一)
圆的面积=圆的周长的一半×半径,如果用S表示圆的面积,r表示圆的半径,那么圆的面积计算公式是S=πr2。
练 习 一
知识点/06 圆的面积(二)
a.
已知圆的半径求圆的面积,直接用公式S=πr2计算即可。若已知圆的直径求圆的面积,则要先用“r=d÷2”求出半径后再计算,或直接用公式S=π(d÷2)2计算。
练 习 一
知识点/06 圆的面积(二)
b.
已知圆的周长求圆的面积,应先利用周长公式C=2πr求出半径,再利用圆的面积公式计算。综合算式为S=π (C÷2π) 2。
c.
圆的面积可以通过把圆形转化成三角形推导出来,圆的面积:S=πr2。
牛刀小试
练 习 一
1.
(1)你能在左面的正方形中画一个面积最大的圆吗?
(2)剪去最大的圆,剩下部分的面积是多少?
4cm
4×4 - 3.14×(4÷2)2
=16 - 3.14×4
=3.44(cm2)
练 习 一
2.填一填。
半径/cm
直径/cm
周长/cm
面积/cm2
0.5
1
9.42
14
3.14
0.785
7.065
153.86
43.96
3
1.5
7
练 习 一
3.
3.14×62=113.04(m2)
练 习 一
4. 某钟表的分针长10cm。
3.14×(10×2)=62.8(厘米)
(1)从1时到2时,分针针尖走过了多少厘米?
3.14×102=314(平方厘米)
(2)从1时到2时,分针扫过的面积是多少平方厘米?
练 习 一
5.要为一个水缸做一个盖子,这个盖子的面积至少是多少平方米?
3.14×(1÷2) 2=0.785(平方米)
答:这个盖子的面积至少是0.785平方米。
练 习 一
6.
12.56÷10÷3.14=0.4(m)
练 习 一
7.常见的自行车车轮的直径如下表。
3.14×559=1755.26(mm)
3.14×610=1915.4(mm)
3.14×660=2072.4(mm)
3.14×711=2232.54(mm)
每种自行车车轮滚动1圈经过的距离分别是多少?
练 习 一
8.长方形的宽是多少厘米?
3.14×(16÷2) 2÷16=12.56(厘米)
练 习 一
9.淘气用两根长度都是62.8cm的铁丝分别围成正方形和圆,它们围成的面积一样大吗?
正方形:62.8÷4=15.7(cm)
15.7×15.7=246.49(cm2)
圆:62.8÷3.14÷2=10(cm)
3.14×102=314(cm2)
因为314>246.49,所以圆的面积大。
练 习 一
10.某汽车车轮的直径为0.5m,汽车行驶到1km时,车轮大约转了多少圈?(结果保留整数)
3.14×0.5=1.57(m)
1km=1000m
1000÷1.57≈637(圈)
答:车轮大约转了637圈。
练 习 一
11.起跑线。
(1)想一想,填一填。
笑笑和淘气分别从A,B处出发,沿半圆走到C,D。他们两人走过的路程一样长吗?
不一样长。
练 习 一
①笑笑所走路线的半径为10m,她走过的路程是 m。
②淘气所走路线的半径为 m,他走过的路程是 m。
③两人走过的路程相差 m。
31.4
3.14
34.54
11
练 习 一
(2)小调查。
在400m比赛中,运动员所在的起跑线位置是不一样的,你知道这是为什么吗?
练 习 一
因为往外一圈的弯道比里面的弯道长,所以运动员的起跑位置会依次向前移相应的距离。调查略。
练 习 一
练 习 一
课堂小结
练 习 一
通过这节课的学习活动,
你有什么收获?
练 习 一
课后作业
2.完成练习册本课时的习题。
1.从课后习题中选取;
谢 谢 观 看
Thanks to watching
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
