数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系(共25张ppt) | 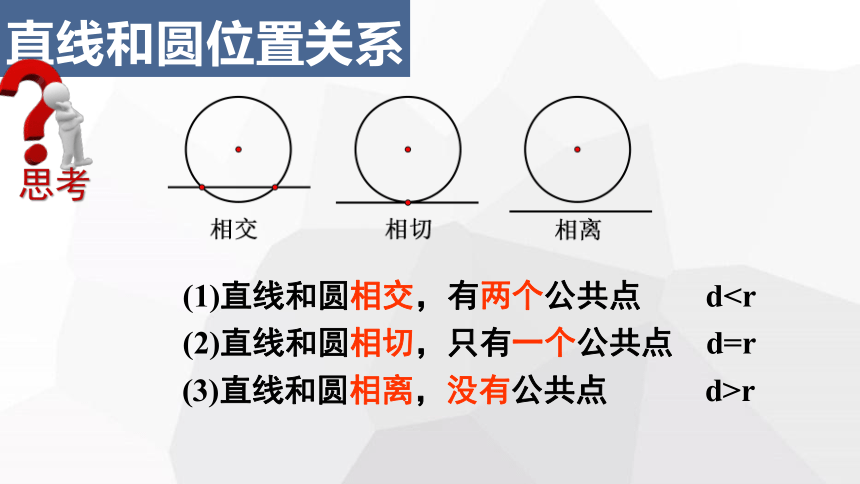 | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 11:06:35 | ||
图片预览








文档简介
(共25张PPT)
(2)直线和圆相切,只有一个公共点 d=r
(1)直线和圆相交,有两个公共点 d(3)直线和圆相离,没有公共点 d>r
直线和圆位置关系
思考
2.5.1 直线和圆的位置关系
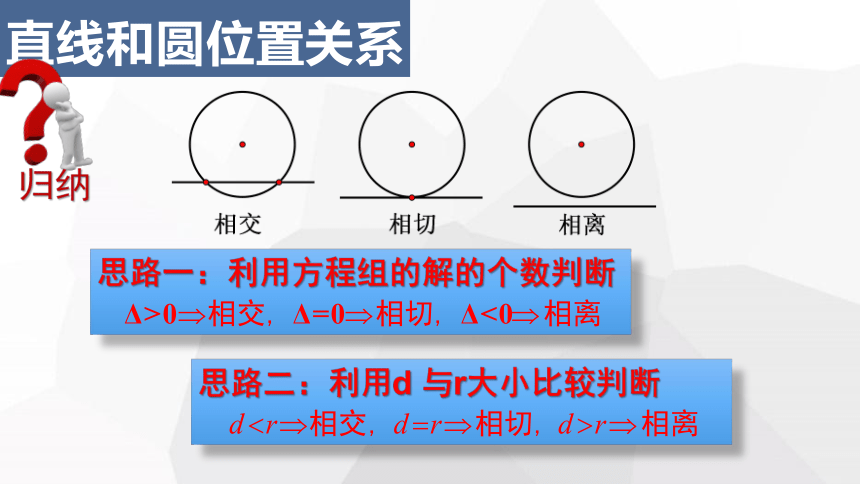
直线和圆位置关系
例1.已知直线l :3x+y-6=0和圆心为C的圆 x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
解:
思路一:
例析
解:
直线和圆位置关系
例析
思路二:
例1.已知直线l :3x+y-6=0和圆心为C的圆 x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
消去y,得:
两直线的位置关系
方程组的解的情况
联立两直线方程
直线与圆的位置关系
联立直线与圆的方程
直线和圆位置关系
思路一:利用方程组的解的个数判断
思路二:利用d 与r大小比较判断
归纳
判断下列直线l与圆C的位置关系
(1)直线l : 3x+4y+2=0 圆C:x2+y2=3
(2)直线l : x+y+3=0 圆C:x2+y2+2y=0
(4)直线l : x=3 圆C:(x-1)2+y2=4
(3)直线l : 3x+4y+2=0 圆C:x2+y2-2x=0
直线和圆位置关系
练习
相交
相离
相切
相切
设切线l的斜率为k,则切线l的方程为
y-1=k(x-2), 即x-y+1-2k=0.
点P在圆外,所以过P有两条切线。
解得 k=0或k=
因此,所求切线l的方程为y=1,或4x-3y-5=0.
解:
直线和圆位置关系
例析
例2.过点P (2,1) 作圆O:x2+y2=1的切线l,求此切线l的方程
由圆心(0,0)到切线l的距离d等于圆的半径1,
直线和圆位置关系
例析
变式1.过点 (1,2) 作圆O:x2+y2=1的切线l,
求此切线l的方程.
变式2.过点 (1,2) 作圆O:x2+y2=5的切线l,
求此切线l的方程.
变式3.过点 (1,1) 作圆O:x2+y2=5的切线l,
求此切线l的方程.
例2.过点P (2,1) 作圆O:x2+y2=1的切线l,求此切线l的方程
x=1 或3x-4y+5=0
x+2y=5
不存在切线
y=1,或4x-3y-5=0
直线和圆位置关系
练习
例2.过点P (1,2) 作圆O:x2+y2=1的切线l,求此切线l的方程
点P在圆外,所以过P有两条切线。
解:
即kx-y+2-k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
设切线l的方程为y-2=k(x-1),
此时,切线l的方程为3x-4y+5=0.
∵直线x=1也符合题意.
故切线l的方程为:x=1 或3x-4y+5=0.
变1.
解:设切线l的斜率为k,
直线和圆位置关系
练习
变式2.过点P (1,2) 作圆O:x2+y2=5的切线l,求此切线l的方程.
所以直线l的方程为:x+2y=5
直线和圆位置关系
练习
变式3.过点P (1,1) 作圆O:x2+y2=5的切线l,求此切线l的方程.
直线和圆位置关系
1.先判断点P与圆的位置关系
2.应用待定系数法设直线方程
时,要注意斜率不存在的情况
归纳
求过一点P的圆的切线方程问题需注意:
若点P在圆上,切线有一条
若点P在圆外,切线有两条
若点P在圆内,没有切线
先定位
再定量
直线和圆位置关系
练习
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
尝试:
直线和圆位置关系
练习
解:
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
直线和圆位置关系
练习
解:
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
r2
变5.
r2
r2
r2
x2→x0x
y2→y0y
直线和圆位置关系
练习
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
r2
变5.
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
变式2.过点P (1,2) 作圆O:x2+y2=5的切线l,求此切线l的方程.
练习
变6.猜一猜:过圆上一点P(x0,y0)的圆C:(x-a)2+(y-b)2=r2的切线方程.
直线和圆位置关系
(x-a)2→(x0-a) (x-a)
(y-b)2→(y0-b) (y-b)
直线和圆位置关系
归纳
过圆上一点P(x0 , y0)的切线方程
可以用变更方程的方法得到
(x-a)2→(x0-a) (x-a)
(y-b)2→(y0-b) (y-b)
已知直线 l :y=x+1,圆C:(x-3)2+y2=1由直线y=x+1上一点P(4, 5)向☉C引切线,求切线长;
直线和圆位置关系
拓展
y
x
1
2
3
4
5
–1
–1
1
2
3
4
5
–2
B
P
A
C
O
已知直线 l :y=x+1,圆C:(x-3)2+y2=1
变式1 :由直线l上任一点P向☉C引切线,
求切线长的最小值
直线和圆位置关系
拓展
y
x
1
2
3
4
5
–1
–1
1
2
3
4
5
–2
B
P
A
C
O
已知直线 l :y=x+1,圆C:(x-3)2+y2=1
变式2 :已知点P为直线l上一动点,过点P作☉C的切线PA,PB,点A,B为切点,则当PC为何值时∠APB最大?
直线和圆位置关系
拓展
y
x
1
2
3
4
5
–1
–1
1
2
3
4
5
–2
B
P
A
C
O
已知直线 l :y=x+1,圆C:(x-3)2+y2=1
变式3 :已知点P为直线l上一动点,过点P作☉C的切线PA,PB,点A,B为切点,求四边形PACB面积的最小值?
直线和圆位置关系
拓展
y
x
1
2
3
4
5
–1
–1
1
2
3
4
5
–2
B
P
A
C
O
1.直线和圆的位置关系判断方法有哪些?
“d,r”法
2. 圆的切线的求解方法?
3. 本节课用到了哪些思想方法?
直线和圆位置关系
小结
待定系数法
数形结合思想方法 方程思想
法
1.教材93页练
2.解决变式问题中的疑惑问题
直线和圆位置关系
作业
谢 谢
(2)直线和圆相切,只有一个公共点 d=r
(1)直线和圆相交,有两个公共点 d
直线和圆位置关系
思考
2.5.1 直线和圆的位置关系
直线和圆位置关系
例1.已知直线l :3x+y-6=0和圆心为C的圆 x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
解:
思路一:
例析
解:
直线和圆位置关系
例析
思路二:
例1.已知直线l :3x+y-6=0和圆心为C的圆 x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
消去y,得:
两直线的位置关系
方程组的解的情况
联立两直线方程
直线与圆的位置关系
联立直线与圆的方程
直线和圆位置关系
思路一:利用方程组的解的个数判断
思路二:利用d 与r大小比较判断
归纳
判断下列直线l与圆C的位置关系
(1)直线l : 3x+4y+2=0 圆C:x2+y2=3
(2)直线l : x+y+3=0 圆C:x2+y2+2y=0
(4)直线l : x=3 圆C:(x-1)2+y2=4
(3)直线l : 3x+4y+2=0 圆C:x2+y2-2x=0
直线和圆位置关系
练习
相交
相离
相切
相切
设切线l的斜率为k,则切线l的方程为
y-1=k(x-2), 即x-y+1-2k=0.
点P在圆外,所以过P有两条切线。
解得 k=0或k=
因此,所求切线l的方程为y=1,或4x-3y-5=0.
解:
直线和圆位置关系
例析
例2.过点P (2,1) 作圆O:x2+y2=1的切线l,求此切线l的方程
由圆心(0,0)到切线l的距离d等于圆的半径1,
直线和圆位置关系
例析
变式1.过点 (1,2) 作圆O:x2+y2=1的切线l,
求此切线l的方程.
变式2.过点 (1,2) 作圆O:x2+y2=5的切线l,
求此切线l的方程.
变式3.过点 (1,1) 作圆O:x2+y2=5的切线l,
求此切线l的方程.
例2.过点P (2,1) 作圆O:x2+y2=1的切线l,求此切线l的方程
x=1 或3x-4y+5=0
x+2y=5
不存在切线
y=1,或4x-3y-5=0
直线和圆位置关系
练习
例2.过点P (1,2) 作圆O:x2+y2=1的切线l,求此切线l的方程
点P在圆外,所以过P有两条切线。
解:
即kx-y+2-k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
设切线l的方程为y-2=k(x-1),
此时,切线l的方程为3x-4y+5=0.
∵直线x=1也符合题意.
故切线l的方程为:x=1 或3x-4y+5=0.
变1.
解:设切线l的斜率为k,
直线和圆位置关系
练习
变式2.过点P (1,2) 作圆O:x2+y2=5的切线l,求此切线l的方程.
所以直线l的方程为:x+2y=5
直线和圆位置关系
练习
变式3.过点P (1,1) 作圆O:x2+y2=5的切线l,求此切线l的方程.
直线和圆位置关系
1.先判断点P与圆的位置关系
2.应用待定系数法设直线方程
时,要注意斜率不存在的情况
归纳
求过一点P的圆的切线方程问题需注意:
若点P在圆上,切线有一条
若点P在圆外,切线有两条
若点P在圆内,没有切线
先定位
再定量
直线和圆位置关系
练习
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
尝试:
直线和圆位置关系
练习
解:
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
直线和圆位置关系
练习
解:
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
r2
变5.
r2
r2
r2
x2→x0x
y2→y0y
直线和圆位置关系
练习
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
r2
变5.
变4.过圆上一点P(x0,y0)作圆O:x2+y2= 5 的切线l,求此切线l的方程.
变式2.过点P (1,2) 作圆O:x2+y2=5的切线l,求此切线l的方程.
练习
变6.猜一猜:过圆上一点P(x0,y0)的圆C:(x-a)2+(y-b)2=r2的切线方程.
直线和圆位置关系
(x-a)2→(x0-a) (x-a)
(y-b)2→(y0-b) (y-b)
直线和圆位置关系
归纳
过圆上一点P(x0 , y0)的切线方程
可以用变更方程的方法得到
(x-a)2→(x0-a) (x-a)
(y-b)2→(y0-b) (y-b)
已知直线 l :y=x+1,圆C:(x-3)2+y2=1由直线y=x+1上一点P(4, 5)向☉C引切线,求切线长;
直线和圆位置关系
拓展
y
x
1
2
3
4
5
–1
–1
1
2
3
4
5
–2
B
P
A
C
O
已知直线 l :y=x+1,圆C:(x-3)2+y2=1
变式1 :由直线l上任一点P向☉C引切线,
求切线长的最小值
直线和圆位置关系
拓展
y
x
1
2
3
4
5
–1
–1
1
2
3
4
5
–2
B
P
A
C
O
已知直线 l :y=x+1,圆C:(x-3)2+y2=1
变式2 :已知点P为直线l上一动点,过点P作☉C的切线PA,PB,点A,B为切点,则当PC为何值时∠APB最大?
直线和圆位置关系
拓展
y
x
1
2
3
4
5
–1
–1
1
2
3
4
5
–2
B
P
A
C
O
已知直线 l :y=x+1,圆C:(x-3)2+y2=1
变式3 :已知点P为直线l上一动点,过点P作☉C的切线PA,PB,点A,B为切点,求四边形PACB面积的最小值?
直线和圆位置关系
拓展
y
x
1
2
3
4
5
–1
–1
1
2
3
4
5
–2
B
P
A
C
O
1.直线和圆的位置关系判断方法有哪些?
“d,r”法
2. 圆的切线的求解方法?
3. 本节课用到了哪些思想方法?
直线和圆位置关系
小结
待定系数法
数形结合思想方法 方程思想
法
1.教材93页练
2.解决变式问题中的疑惑问题
直线和圆位置关系
作业
谢 谢
