人教版数学九年级上册 24.3 正多边形和圆(第1课时)教案
文档属性
| 名称 | 人教版数学九年级上册 24.3 正多边形和圆(第1课时)教案 |  | |
| 格式 | docx | ||
| 文件大小 | 621.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 11:43:35 | ||
图片预览




文档简介
24.3 正多边形和圆
第1课时
一、教学目标
【知识与技能】
了解正多边形和圆的关系,了解正多边形半径和边长,边心距,中心,中心角等概念.会应用正多边形的有关知识解决圆中的计算问题.
【过程与方法】
结合生活中的正多边形形状的图案,发现正多边形和圆的关系.
【情感态度与价值观】
学生经历观察、发现、探究等数学活动,感受到数学来源于生活、又服务于生活.
二、课型
新授课
三、课时
第1课时,共2课时。
四、教学重难点
【教学重点】
正多边形与圆的相关概念及其之间的运算.
【教学难点】
探索正多边形和圆的关系,正多边形半径,中心角、边心距,边长之间的关系.
五、课前准备
课件、图片、直尺等.
六、教学过程
(一)导入新课
出示课件2,3:
观察上边的美丽图案,思考下面的问题:
(1)这些都是生活中经常见到的利用正多边形得到的物体,你能找出正多边形吗?
(2)你知道正多边形和圆有什么关系吗?怎样做一个正多边形呢?
学生通过观察美丽的图案,欣赏生活中正多边形形状的物体.让学生感受到数学来源于生活,并从中感受到数学美.(板书课题)
(二)探索新知
探究一 正多边形的对称性
教师问:什么叫做正多边形?(出示课件5)
学生答:各边相等,各角也相等的多边形叫做正多边形.
教师问:矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
学生答:矩形不是正多边形,因为矩形不符合各边相等;菱形不是正多边形,因为菱形不符合各角相等;
教师强调:正多边形:①各边相等;②各角相等,两个条件,缺一不可.
教师问:正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?(出示课件6,7)
学生动手操作,交流,感受正多边形的对称性.
教师归纳:正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形既是轴对称图形又是中心对称图形.
探究二 正多边形的有关概念
教师问:以正四边形为例,根据对称轴的性质,你能得出什么结论?(出示课件8,9)
师生结合图形共同探究:
EF是边AB、CD的垂直平分线,∴OA=OB,OD=OC.
GH是边AD、BC的垂直平分线,
∴OA=OD,OB=OC.
∴OA=OB=OC=OD.
∴正方形ABCD有一个以点O为圆心的外接圆.
AC是∠DAB及∠DCB的角平分线,BD是∠ABC及∠ADC的角平分线,
∴OE=OH=OF=OG.
∴正方形ABCD还有一个以点O为圆心的内切圆.
出示课件10:
教师问:所有的正多边形是不是也都有一个外接圆和一个内切圆?
学生答:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.
教师问:一个正多边形的各个顶点在同一个圆上
学生答:一个正多边形的各个顶点在同一个圆上,则这个正多边形就是这个圆的一个内接正多边形,圆叫做这个正多边形的外接圆.
教师问:所有的多边形是不是都有一个外接圆和内切圆?
学生答:多边形不一定有外接圆和内切圆,只有是正多边形时才有,任意三角形都有外接圆和内切圆.
教师出示概念:(出示课件11)
1.正多边形的外接圆和内切圆的公共圆心,叫做正多边形的中心.
2.外接圆的半径叫做正多边形的半径.
3.内切圆的半径叫做正多边形的边心距.
4.正多边形每一条边所对的圆心角,叫做正多边形的中心角.正多边形的每个中心角都等于
练一练:(出示课件12)完成下面的表格:
正多边形边数 内角 中心角 外角
3
4
6
n
学生计算交流并填表.
探究三 正多边形的有关计算
出示课件13:如图,已知半径为4的圆内接正六边形ABCDEF:
①它的中心角等于 度;
②OC BC(填>、<或=);
③△OBC是 三角形;
④圆内接正六边形的面积是△OBC面积的 倍.
⑤圆内接正n边形面积公式:_______________________.
学生计算交流后,教师抽学生口答.
①60;②=;③等边;④6;⑤
出示课件14:例 有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
教师分析:根据题意作图,将实际问题转化为数学问题.师生共同解答:(出示课件15)
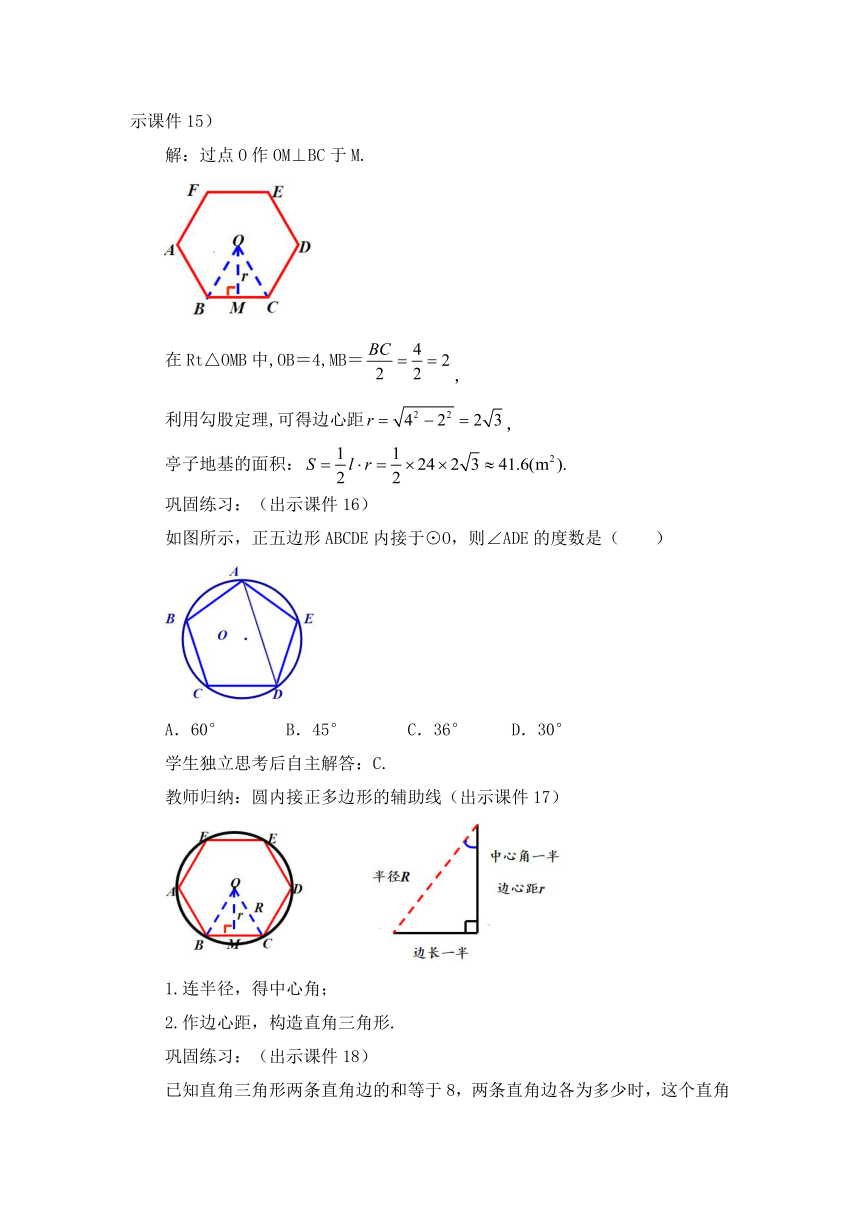
解:过点O作OM⊥BC于M.
在Rt△OMB中,OB=4,MB=,
利用勾股定理,可得边心距,
亭子地基的面积:
巩固练习:(出示课件16)
如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是( )
A.60° B.45° C.36° D.30°
学生独立思考后自主解答:C.
教师归纳:圆内接正多边形的辅助线(出示课件17)
1.连半径,得中心角;
2.作边心距,构造直角三角形.
巩固练习:(出示课件18)
已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?
学生独立思考后解答,一生板演.
解:∵直角三角形两直角边之和为8,设一边长为x.
∴ 另一边长为8-x.
则该直角三角形面积:S=(8-x)x÷2,即
当x==4,另一边为4时,S有最大值=8.
∴当两直角边都是4时,直角面积最大,最大值为8.
(三)课堂练习(出示课件19-24)
1.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=______度.
2.填表:
正多边形边数 半径 边长 边心距 周长 面积
3
4 1
6
3.若正多边形的边心距与半径的比为1:2,则这个多边形的边数是_____.
4.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为_____度.(不取近似值)
5.要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
6.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
7.如图,正六边形ABCDEF的边长为,点P为六边形内任一点.则点P到各边距离之和是多少?
8.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON=_______;图②中∠MON=_______;图③中∠MON=_______;
(2)试探究∠MON的度数与正n边形的边数n的关系.
参考答案:
1.360°解析:由多边形的外角和等于360°可知,∠1+∠2+∠3+∠4+∠5=360°.
2.
3.3
4.
5.
6.解:∵正方形的面积等于4,
∴正方形的边长AB=2.
则圆的直径AC=2,
∴⊙O的半径=.
∴⊙O的面积为
7.解:过P作AB的垂线,分别交AB、DE于H、K,连接BD,作CG⊥BD于G.
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,
∴P到AF与CD的距离之和,及P到EF、BC的距离之和均为HK的长.
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,BD∥HK,且BD=HK.
∴CG=BC=.
∵CG⊥BD,
∴BD=2BG=2×=2×3=6.
∴点P到各边距离之和=3BD=3×6=18.
8.解:⑴①120°;②90°;③72°;
⑵.
(四)课堂小结
通过这节课的学习,你知道正多边形和圆有怎样的关系吗?你知道正多边形的半径、边心距、内角、中心角等概念吗?
(五)课前预习
预习下节课(24.3第2课时)的相关内容.
七、课后作业
配套练习册内容
八、板书设计:
九、教学反思:
本节课通过创设问题情境,将正多边形与圆紧密联系,让学生发现它们之间的密切关系,并将结论由特殊推广到一般,符合学生的认识规律,通过学习正多边形中的一些基本概念,引导学生将实际问题转化为数学问题,体现了化归的思想.
第1课时
一、教学目标
【知识与技能】
了解正多边形和圆的关系,了解正多边形半径和边长,边心距,中心,中心角等概念.会应用正多边形的有关知识解决圆中的计算问题.
【过程与方法】
结合生活中的正多边形形状的图案,发现正多边形和圆的关系.
【情感态度与价值观】
学生经历观察、发现、探究等数学活动,感受到数学来源于生活、又服务于生活.
二、课型
新授课
三、课时
第1课时,共2课时。
四、教学重难点
【教学重点】
正多边形与圆的相关概念及其之间的运算.
【教学难点】
探索正多边形和圆的关系,正多边形半径,中心角、边心距,边长之间的关系.
五、课前准备
课件、图片、直尺等.
六、教学过程
(一)导入新课
出示课件2,3:
观察上边的美丽图案,思考下面的问题:
(1)这些都是生活中经常见到的利用正多边形得到的物体,你能找出正多边形吗?
(2)你知道正多边形和圆有什么关系吗?怎样做一个正多边形呢?
学生通过观察美丽的图案,欣赏生活中正多边形形状的物体.让学生感受到数学来源于生活,并从中感受到数学美.(板书课题)
(二)探索新知
探究一 正多边形的对称性
教师问:什么叫做正多边形?(出示课件5)
学生答:各边相等,各角也相等的多边形叫做正多边形.
教师问:矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
学生答:矩形不是正多边形,因为矩形不符合各边相等;菱形不是正多边形,因为菱形不符合各角相等;
教师强调:正多边形:①各边相等;②各角相等,两个条件,缺一不可.
教师问:正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?(出示课件6,7)
学生动手操作,交流,感受正多边形的对称性.
教师归纳:正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形既是轴对称图形又是中心对称图形.
探究二 正多边形的有关概念
教师问:以正四边形为例,根据对称轴的性质,你能得出什么结论?(出示课件8,9)
师生结合图形共同探究:
EF是边AB、CD的垂直平分线,∴OA=OB,OD=OC.
GH是边AD、BC的垂直平分线,
∴OA=OD,OB=OC.
∴OA=OB=OC=OD.
∴正方形ABCD有一个以点O为圆心的外接圆.
AC是∠DAB及∠DCB的角平分线,BD是∠ABC及∠ADC的角平分线,
∴OE=OH=OF=OG.
∴正方形ABCD还有一个以点O为圆心的内切圆.
出示课件10:
教师问:所有的正多边形是不是也都有一个外接圆和一个内切圆?
学生答:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.
教师问:一个正多边形的各个顶点在同一个圆上
学生答:一个正多边形的各个顶点在同一个圆上,则这个正多边形就是这个圆的一个内接正多边形,圆叫做这个正多边形的外接圆.
教师问:所有的多边形是不是都有一个外接圆和内切圆?
学生答:多边形不一定有外接圆和内切圆,只有是正多边形时才有,任意三角形都有外接圆和内切圆.
教师出示概念:(出示课件11)
1.正多边形的外接圆和内切圆的公共圆心,叫做正多边形的中心.
2.外接圆的半径叫做正多边形的半径.
3.内切圆的半径叫做正多边形的边心距.
4.正多边形每一条边所对的圆心角,叫做正多边形的中心角.正多边形的每个中心角都等于
练一练:(出示课件12)完成下面的表格:
正多边形边数 内角 中心角 外角
3
4
6
n
学生计算交流并填表.
探究三 正多边形的有关计算
出示课件13:如图,已知半径为4的圆内接正六边形ABCDEF:
①它的中心角等于 度;
②OC BC(填>、<或=);
③△OBC是 三角形;
④圆内接正六边形的面积是△OBC面积的 倍.
⑤圆内接正n边形面积公式:_______________________.
学生计算交流后,教师抽学生口答.
①60;②=;③等边;④6;⑤
出示课件14:例 有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
教师分析:根据题意作图,将实际问题转化为数学问题.师生共同解答:(出示课件15)
解:过点O作OM⊥BC于M.
在Rt△OMB中,OB=4,MB=,
利用勾股定理,可得边心距,
亭子地基的面积:
巩固练习:(出示课件16)
如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是( )
A.60° B.45° C.36° D.30°
学生独立思考后自主解答:C.
教师归纳:圆内接正多边形的辅助线(出示课件17)
1.连半径,得中心角;
2.作边心距,构造直角三角形.
巩固练习:(出示课件18)
已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?
学生独立思考后解答,一生板演.
解:∵直角三角形两直角边之和为8,设一边长为x.
∴ 另一边长为8-x.
则该直角三角形面积:S=(8-x)x÷2,即
当x==4,另一边为4时,S有最大值=8.
∴当两直角边都是4时,直角面积最大,最大值为8.
(三)课堂练习(出示课件19-24)
1.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=______度.
2.填表:
正多边形边数 半径 边长 边心距 周长 面积
3
4 1
6
3.若正多边形的边心距与半径的比为1:2,则这个多边形的边数是_____.
4.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为_____度.(不取近似值)
5.要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
6.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
7.如图,正六边形ABCDEF的边长为,点P为六边形内任一点.则点P到各边距离之和是多少?
8.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON=_______;图②中∠MON=_______;图③中∠MON=_______;
(2)试探究∠MON的度数与正n边形的边数n的关系.
参考答案:
1.360°解析:由多边形的外角和等于360°可知,∠1+∠2+∠3+∠4+∠5=360°.
2.
3.3
4.
5.
6.解:∵正方形的面积等于4,
∴正方形的边长AB=2.
则圆的直径AC=2,
∴⊙O的半径=.
∴⊙O的面积为
7.解:过P作AB的垂线,分别交AB、DE于H、K,连接BD,作CG⊥BD于G.
∵六边形ABCDEF是正六边形,
∴AB∥DE,AF∥CD,BC∥EF,
∴P到AF与CD的距离之和,及P到EF、BC的距离之和均为HK的长.
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,BD∥HK,且BD=HK.
∴CG=BC=.
∵CG⊥BD,
∴BD=2BG=2×=2×3=6.
∴点P到各边距离之和=3BD=3×6=18.
8.解:⑴①120°;②90°;③72°;
⑵.
(四)课堂小结
通过这节课的学习,你知道正多边形和圆有怎样的关系吗?你知道正多边形的半径、边心距、内角、中心角等概念吗?
(五)课前预习
预习下节课(24.3第2课时)的相关内容.
七、课后作业
配套练习册内容
八、板书设计:
九、教学反思:
本节课通过创设问题情境,将正多边形与圆紧密联系,让学生发现它们之间的密切关系,并将结论由特殊推广到一般,符合学生的认识规律,通过学习正多边形中的一些基本概念,引导学生将实际问题转化为数学问题,体现了化归的思想.
同课章节目录
