1.6中位线定理（第2课时）

九年级上学期数学学科新课改教学案
课题:§1.6中位线定理（第2课时）
梯形的中位线
修订人:初中数学教学案编写组
【教学目标】
1.理解三角形中位线的概念，掌握它的性质定理。
2.会证明三角形中位线定理，并能熟练地应用它进行有关的证明和计算。
【重点与难点】
三角形中位线定理的证明。
教学过程：
【复习回顾】
1．连结三角形 的线段，叫做三角形的中位线；
2．三角形的中位线 第三边，且等于第三边的 。
试一试：
（上海）在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，则四边形EFGH是 四边形。
若AC=BD，则四边形EFGH是 四边形；
若AC⊥BD，则四边形EFGH是 四边形；
若AC=BD且AC⊥BD，则四边形EFGH是 四边形。
【探索新知】
阅读课本第36页至38页，完成以下内容：
1．梯形的中位线
连接 的线段叫做梯形的中位线。
2．梯形的中位线定理
梯形的中位线平行于 ，且等于 的一半。
已知：梯形ABCD中，AD∥BC，EF为梯形的中位线；
求证：①AD∥EF∥BC，
②
证明：
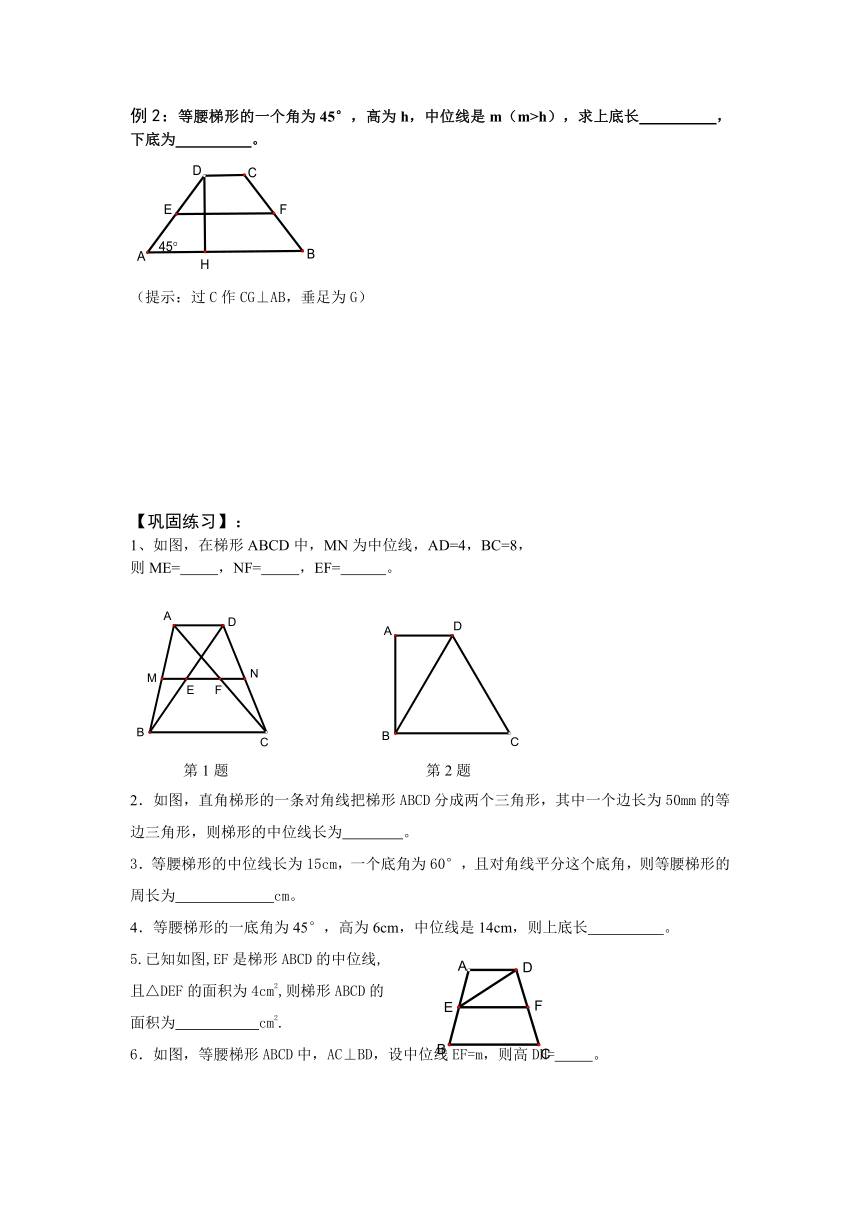
例2：等腰梯形的一个角为45°，高为h，中位线是m（m>h），求上底长 ，下底为 。
（提示：过C作CG⊥AB，垂足为G）
【巩固练习】：
1、如图，在梯形ABCD中，MN为中位线，AD=4，BC=8，
则ME= ，NF= ，EF= 。
第1题 第2题
2．如图，直角梯形的一条对角线把梯形ABCD分成两个三角形，其中一个边长为50mm的等边三角形，则梯形的中位线长为 。
3．等腰梯形的中位线长为15cm，一个底角为60°，且对角线平分这个底角，则等腰梯形的周长为 cm。
4．等腰梯形的一底角为45°，高为6cm，中位线是14cm，则上底长 。
5.已知如图,EF是梯形ABCD的中位线,
且△DEF的面积为4cm2,则梯形ABCD的
面积为 cm2.
6．如图，等腰梯形ABCD中，AC⊥BD，设中位线EF=m，则高DH= 。
第6题 第7题
7.已知如图，梯形ABCD中，AD∥BC，E为AB的中点，且∠DEC=90°；
求证：DC=AD+BC.
【感悟与收获】
梯形的中位线：
连接梯形 的线段，叫做梯形的中位线；
梯形的中位线定理：
梯形的中位线平行于 ，且等于 的一半。
【课后拓展】：
在梯形ABCD中,ABCD,E、F为对角线的中点,
AD=2,BC=6,求EF.
（提示：连结AE，并延长AE交BC于G）
归纳结论：
连结梯形对角线中点的线段平行于梯形的 ，
且等于 的一半。（下底>上底）
【教学反思】：