2022-2023学年七年级数学上册6.3 一次函数的图象(2) 教案
文档属性
| 名称 | 2022-2023学年七年级数学上册6.3 一次函数的图象(2) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 319.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 10:24:04 | ||
图片预览


文档简介
6.3 一次函数的图象(2)
一.教学目标
(一)教学知识点
1.理解一次函数的代数表达式与图象之间的对应关系.
2.能熟练作出一次函数的图象.
(二)能力训练要求
1.已知解析式作函数的图象,培养学生数形结合的意识和能力.
2.在探究活动中发展学生的合作意识和能力.
(三)情感与价值观要求
1.经历作图过程,归纳总结作函数图象的一般步骤,发展学生的总结概括能力.
2.加强新旧知识的联系,促进学生新的认知结构的建构.
二.教学重点
1.能熟练地作出一次函数的图象.
2.归纳作函数图象的一般步骤.
3.理解一次函数的代数表达式与图象之间的对应关系.
三.教学难点
理解一次函数的代数表达式与图象之间的对应关系.
四.教学方法
讲、议结合法.
五.教具准备
投影片两张:
第一张:补充练习(§6.3.2 A );
第二张:补充练习(§6.3.2 B).
六.教学过程
Ⅰ.知识回顾
[师]上节课我们学习了正比例函数的图象画法及其性质,请大家回忆一下:
1.作函数图象有几个主要步骤?
2.上节课中我们探究得到正比例函数图象有什么特征?
3.作一次函数图象需要描出几个点?
[生]1. ①列表;②描点;③连线.
2. (1)正比例函数的图象都经过坐标原点。
(2)在正比例函数y=kx的图象中,当k>0时,y的值随x值的增大而增大;当k<0时,y的值随x值的增大而减小。
3.作正比例函数y=kx的图象时,除原点外,还需找一点,一般找(1,k)点。
[师]非常好!看来大家掌握的不错,那么,一般的一次函数的图象又是怎样的呢?
Ⅱ.讲授新课
一、作一次函数的图象
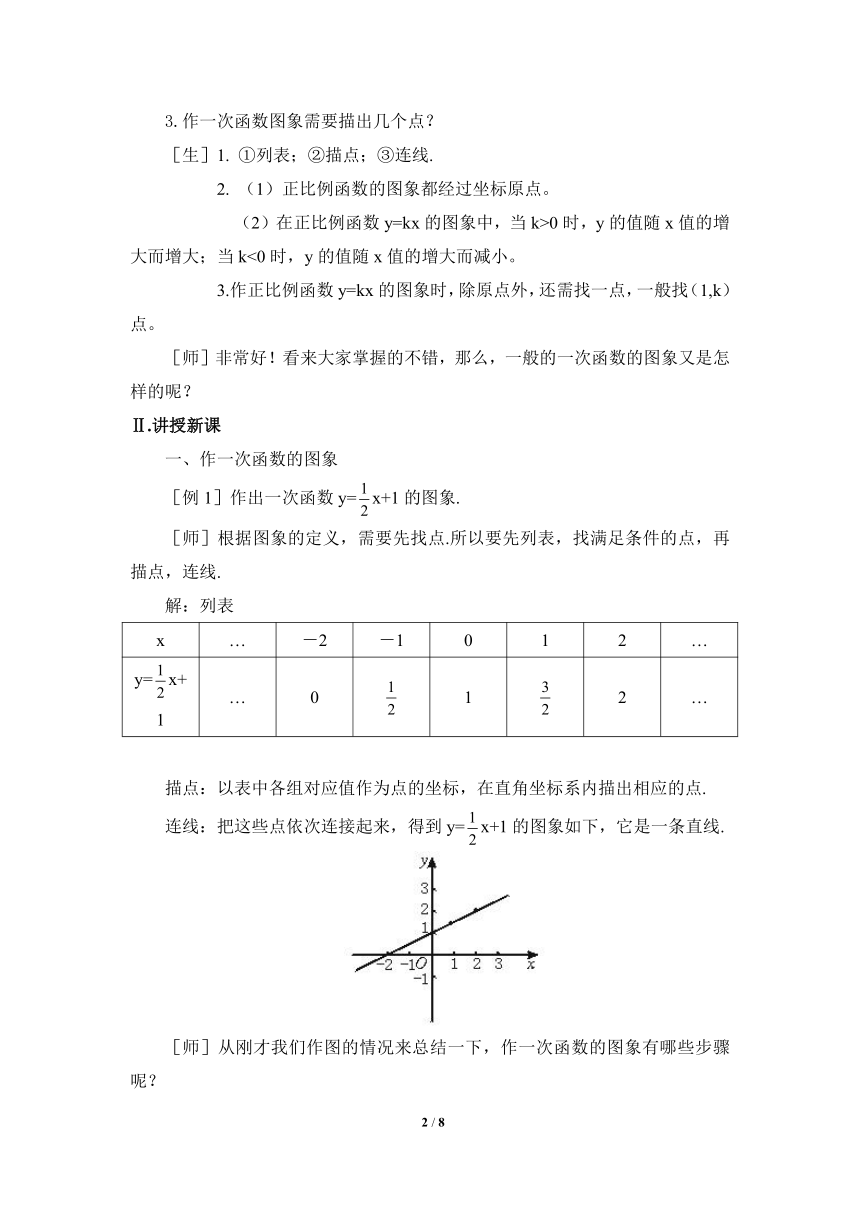
[例1]作出一次函数y=x+1的图象.
[师]根据图象的定义,需要先找点.所以要先列表,找满足条件的点,再描点,连线.
解:列表
x … -2 -1 0 1 2 …
y=x+1 … 0 1 2 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
连线:把这些点依次连接起来,得到y=x+1的图象如下,它是一条直线.
[师]从刚才我们作图的情况来总结一下,作一次函数的图象有哪些步骤呢?
[生]①列表;②描点;③连线.
二、做一做
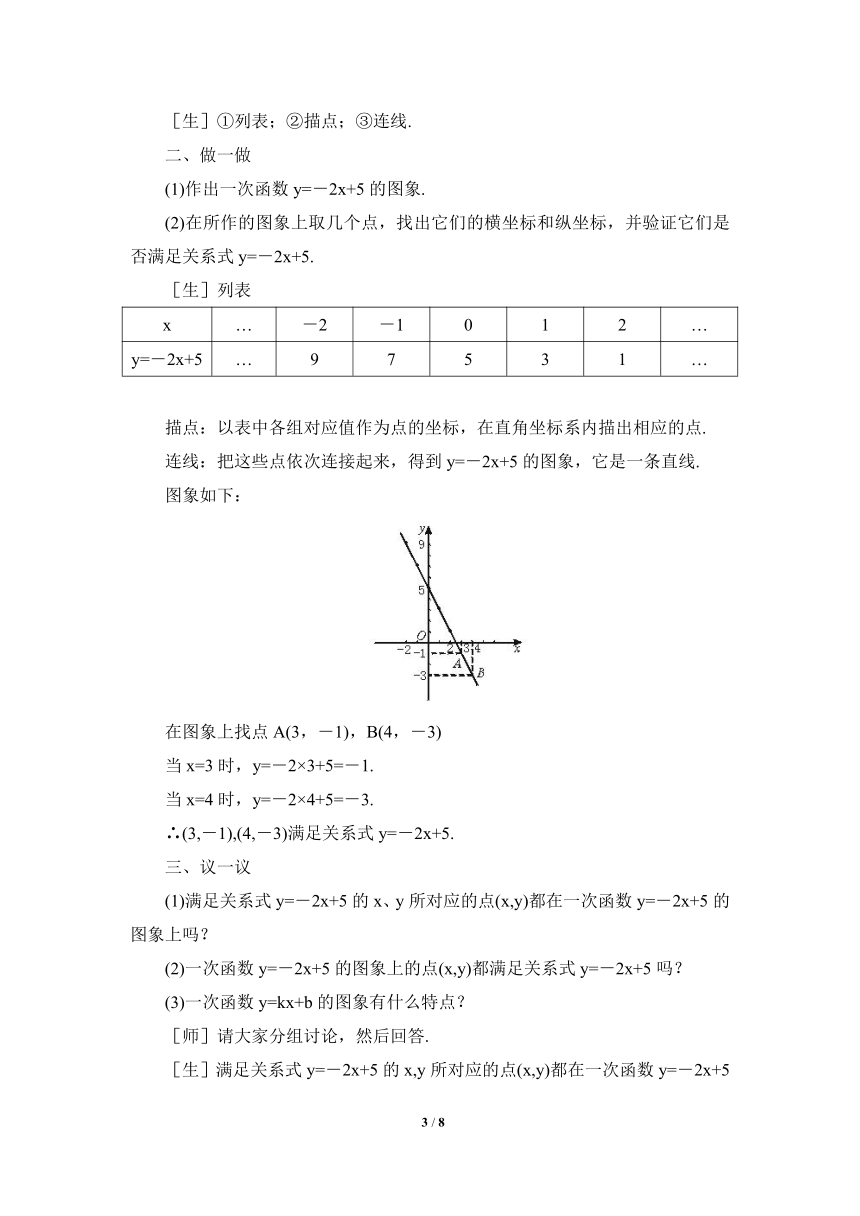
(1)作出一次函数y=-2x+5的图象.
(2)在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否满足关系式y=-2x+5.
[生]列表
x … -2 -1 0 1 2 …
y=-2x+5 … 9 7 5 3 1 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
连线:把这些点依次连接起来,得到y=-2x+5的图象,它是一条直线.
图象如下:
在图象上找点A(3,-1),B(4,-3)
当x=3时,y=-2×3+5=-1.
当x=4时,y=-2×4+5=-3.
∴(3,-1),(4,-3)满足关系式y=-2x+5.
三、议一议
(1)满足关系式y=-2x+5的x、y所对应的点(x,y)都在一次函数y=-2x+5的图象上吗?
(2)一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5吗?
(3)一次函数y=kx+b的图象有什么特点?
[师]请大家分组讨论,然后回答.
[生]满足关系式y=-2x+5的x,y所对应的点(x,y)都在一次函数y=-2x+5的图象上.
(2)一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5.
[师]由此看来,满足函数关系式y=-2x+5的x,y所对应的点(x,y)都在一次函数y=-2x+5的图象上;反过来,一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5.
所以,一次函数的代数表达式与图象是一一对应的.即满足一次函数的代数表达式的点在图象上,图象上的每一点的横坐标x,纵坐标y都满足一次函数的代数表达式.
(3)[生]一次函数的图象是一条直线.
[师]非常正确.
一次函数的图象是一条直线.由直线的公理可知:两点确定一条直线,所以作一次函数的图象时,只要确定两个点,再过这两个点作直线就可以了,一次函数y=kx+b的图象也称为直线y=kx+b.
Ⅲ.课堂练习
分别作出一次函数y=x与y=-3x+9的图象.
[师]根据刚才的讨论可知,我们在画一次函数的图象时,只要确定两个点就可以了.
[生]作函数y=x的图象时,找点(3,1),(6,2)图象如下.
作函数y=-3x+9的图象时,找点(1,6),(2,3)
图象如下:
补充练习
投影片(§6.3.2A)
(1)作出一次函数y=-x+的图象.(2)在所作的图象上取几个点,找出它们的坐标,并验证其是否都满足关系式y=-x+.
[生](1)作一次函数y=-x+的图象时,取点(0, )和(1,-),然后过这两点作直线即可.图象如下:
(2)在图象上取点A(,-1),B(-1,)
当x=时,y=-+ =-1
当x=-1时,y=1+=
∴A、B两点的坐标都满足关系式y=-x+.
投影片(§6.3.2B)
(1)作出一次函数y=4x+3的图象;(2)判断下列各对数是不是满足关系式y=4x+3,如果是,请验证一下以这些数对为坐标的点是否在你所作出的函数图象上.(0,3),(-1,-1),(,5),(1,7),(-,-3)
[生]解:(1)作一次函数y=4x+3的图象时,找点(0,3),(1,7),然后过这两点作直线即可.图象如下:
(2)当x=0时,y=4×0+3=3;
当x=-1时,y=4×(-1)+3=-1;
当x=时,y=4×+3=5;
当x=1时,y=4×1+3=7;
当x=-时,y=4×(-)+3=-3.
∴每对数都满足关系式y=4x+3.
由前面的议一议可知,以这些数对为坐标的点在所作的函数图象上.
Ⅳ.课时小结
本节课主要学习了以下内容:
1.作一次函数图象的步骤以及熟练地作出一次函数的图象,并能验证某些数对是否在函数图象上.
2.明确一次函数的图象是一条直线,因此在作一次函数的图象时,不需要列表,只要确定两点就可以了.
Ⅴ.课后作业
习题6.4
Ⅵ.活动与探究
1.已知函数y=(m-2)x+m-4,问当m为何值时,它是一次函数?
解:根据一次函数的定义,有
解得
∴m=1或m=4
2.如果y+3与x+2成正比例,且x=3时,y=7.
①写出y与x之间的函数关系式;
②求当x=-1时,y的值;
③求当y=0时,x的值.
分析:①y+3与x+2成正比例,就是y+3=k·(x+2),根据x=3时,y=7,求k的值,从而确定y与x之间的函数关系式.
②把x=-1代入所求函数关系式,求出y的值.
③把y=0代入函数关系式,求出x的值.
解:
①∵y+3与x+2成正比例
∴y+3=k(x+2)
把x=3,y=7代入得:7+3=k(3+2)
∴k=2,∴y=2x+1
②把x=-1代入y=2x+1中,得
y=-2+1=-1
③把y=0代入y=2x+1中,得
0=2x+1,∴x=-.
说明:若y与x成一次函数关系式,那么函数关系式要写成y=kx+b(k≠0)的形式.
3.如果y=mx是正比例函数,而且对于它的每一组非零的对应值(x,y)有xy<0,求m的值.
分析:按正比例函数y=kx(k≠0)中对于k及x的指数的要求决定m的值.
解:根据题意得,y=mx是正比例函数,故有:m2-8=1且m≠0
即m=3或m=-3
又∵xy<0,∴x,y是异号.
∴m=<0
∴m=3不合题意,舍去.
∴m=-3.
常见错误:忽略m≠0的要求,在解题过程不写这一条件.
4.已知y+b与x+a(a,b是常数)成正比例.
求证:y是x的一次函数.
分析:由y+b与x+a成正比例,设立解析式,分析此解析式为x的一次函数.
解:∵y+b与x+a成正比例
∴可设y+b=k(x+a)(k≠0)
整理,得y=kx+ka-b=kx+(ka-b)
∵k,a,b都是常数.∴ka-b也是常数.
又∵k≠0
∴y是x的一次函数.
常见错误:整理得到y=kx+ka-b时不会把ka-b看作一个整式.
说明:在叙述函数的,一定要说清楚谁是谁的什么名称函数,否则容易发生混淆现象.如本题中,y+b是x+a的正比例这个说法是正确的,同时,y是x的一次函数的说法也是正确的.
七.板书设计
§6.3 一次函数的图象(2)一、如何作一次函数的图象归纳步骤二、做一做(作一次函数的图象)三、议一议(函数y=-2x+5的图象与满足y=-2x+5的x,y所对应的点(x,y)之间的关系)四、课堂练习五、课时小节六、课后作业
6 / 8
一.教学目标
(一)教学知识点
1.理解一次函数的代数表达式与图象之间的对应关系.
2.能熟练作出一次函数的图象.
(二)能力训练要求
1.已知解析式作函数的图象,培养学生数形结合的意识和能力.
2.在探究活动中发展学生的合作意识和能力.
(三)情感与价值观要求
1.经历作图过程,归纳总结作函数图象的一般步骤,发展学生的总结概括能力.
2.加强新旧知识的联系,促进学生新的认知结构的建构.
二.教学重点
1.能熟练地作出一次函数的图象.
2.归纳作函数图象的一般步骤.
3.理解一次函数的代数表达式与图象之间的对应关系.
三.教学难点
理解一次函数的代数表达式与图象之间的对应关系.
四.教学方法
讲、议结合法.
五.教具准备
投影片两张:
第一张:补充练习(§6.3.2 A );
第二张:补充练习(§6.3.2 B).
六.教学过程
Ⅰ.知识回顾
[师]上节课我们学习了正比例函数的图象画法及其性质,请大家回忆一下:
1.作函数图象有几个主要步骤?
2.上节课中我们探究得到正比例函数图象有什么特征?
3.作一次函数图象需要描出几个点?
[生]1. ①列表;②描点;③连线.
2. (1)正比例函数的图象都经过坐标原点。
(2)在正比例函数y=kx的图象中,当k>0时,y的值随x值的增大而增大;当k<0时,y的值随x值的增大而减小。
3.作正比例函数y=kx的图象时,除原点外,还需找一点,一般找(1,k)点。
[师]非常好!看来大家掌握的不错,那么,一般的一次函数的图象又是怎样的呢?
Ⅱ.讲授新课
一、作一次函数的图象
[例1]作出一次函数y=x+1的图象.
[师]根据图象的定义,需要先找点.所以要先列表,找满足条件的点,再描点,连线.
解:列表
x … -2 -1 0 1 2 …
y=x+1 … 0 1 2 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
连线:把这些点依次连接起来,得到y=x+1的图象如下,它是一条直线.
[师]从刚才我们作图的情况来总结一下,作一次函数的图象有哪些步骤呢?
[生]①列表;②描点;③连线.
二、做一做
(1)作出一次函数y=-2x+5的图象.
(2)在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否满足关系式y=-2x+5.
[生]列表
x … -2 -1 0 1 2 …
y=-2x+5 … 9 7 5 3 1 …
描点:以表中各组对应值作为点的坐标,在直角坐标系内描出相应的点.
连线:把这些点依次连接起来,得到y=-2x+5的图象,它是一条直线.
图象如下:
在图象上找点A(3,-1),B(4,-3)
当x=3时,y=-2×3+5=-1.
当x=4时,y=-2×4+5=-3.
∴(3,-1),(4,-3)满足关系式y=-2x+5.
三、议一议
(1)满足关系式y=-2x+5的x、y所对应的点(x,y)都在一次函数y=-2x+5的图象上吗?
(2)一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5吗?
(3)一次函数y=kx+b的图象有什么特点?
[师]请大家分组讨论,然后回答.
[生]满足关系式y=-2x+5的x,y所对应的点(x,y)都在一次函数y=-2x+5的图象上.
(2)一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5.
[师]由此看来,满足函数关系式y=-2x+5的x,y所对应的点(x,y)都在一次函数y=-2x+5的图象上;反过来,一次函数y=-2x+5的图象上的点(x,y)都满足关系式y=-2x+5.
所以,一次函数的代数表达式与图象是一一对应的.即满足一次函数的代数表达式的点在图象上,图象上的每一点的横坐标x,纵坐标y都满足一次函数的代数表达式.
(3)[生]一次函数的图象是一条直线.
[师]非常正确.
一次函数的图象是一条直线.由直线的公理可知:两点确定一条直线,所以作一次函数的图象时,只要确定两个点,再过这两个点作直线就可以了,一次函数y=kx+b的图象也称为直线y=kx+b.
Ⅲ.课堂练习
分别作出一次函数y=x与y=-3x+9的图象.
[师]根据刚才的讨论可知,我们在画一次函数的图象时,只要确定两个点就可以了.
[生]作函数y=x的图象时,找点(3,1),(6,2)图象如下.
作函数y=-3x+9的图象时,找点(1,6),(2,3)
图象如下:
补充练习
投影片(§6.3.2A)
(1)作出一次函数y=-x+的图象.(2)在所作的图象上取几个点,找出它们的坐标,并验证其是否都满足关系式y=-x+.
[生](1)作一次函数y=-x+的图象时,取点(0, )和(1,-),然后过这两点作直线即可.图象如下:
(2)在图象上取点A(,-1),B(-1,)
当x=时,y=-+ =-1
当x=-1时,y=1+=
∴A、B两点的坐标都满足关系式y=-x+.
投影片(§6.3.2B)
(1)作出一次函数y=4x+3的图象;(2)判断下列各对数是不是满足关系式y=4x+3,如果是,请验证一下以这些数对为坐标的点是否在你所作出的函数图象上.(0,3),(-1,-1),(,5),(1,7),(-,-3)
[生]解:(1)作一次函数y=4x+3的图象时,找点(0,3),(1,7),然后过这两点作直线即可.图象如下:
(2)当x=0时,y=4×0+3=3;
当x=-1时,y=4×(-1)+3=-1;
当x=时,y=4×+3=5;
当x=1时,y=4×1+3=7;
当x=-时,y=4×(-)+3=-3.
∴每对数都满足关系式y=4x+3.
由前面的议一议可知,以这些数对为坐标的点在所作的函数图象上.
Ⅳ.课时小结
本节课主要学习了以下内容:
1.作一次函数图象的步骤以及熟练地作出一次函数的图象,并能验证某些数对是否在函数图象上.
2.明确一次函数的图象是一条直线,因此在作一次函数的图象时,不需要列表,只要确定两点就可以了.
Ⅴ.课后作业
习题6.4
Ⅵ.活动与探究
1.已知函数y=(m-2)x+m-4,问当m为何值时,它是一次函数?
解:根据一次函数的定义,有
解得
∴m=1或m=4
2.如果y+3与x+2成正比例,且x=3时,y=7.
①写出y与x之间的函数关系式;
②求当x=-1时,y的值;
③求当y=0时,x的值.
分析:①y+3与x+2成正比例,就是y+3=k·(x+2),根据x=3时,y=7,求k的值,从而确定y与x之间的函数关系式.
②把x=-1代入所求函数关系式,求出y的值.
③把y=0代入函数关系式,求出x的值.
解:
①∵y+3与x+2成正比例
∴y+3=k(x+2)
把x=3,y=7代入得:7+3=k(3+2)
∴k=2,∴y=2x+1
②把x=-1代入y=2x+1中,得
y=-2+1=-1
③把y=0代入y=2x+1中,得
0=2x+1,∴x=-.
说明:若y与x成一次函数关系式,那么函数关系式要写成y=kx+b(k≠0)的形式.
3.如果y=mx是正比例函数,而且对于它的每一组非零的对应值(x,y)有xy<0,求m的值.
分析:按正比例函数y=kx(k≠0)中对于k及x的指数的要求决定m的值.
解:根据题意得,y=mx是正比例函数,故有:m2-8=1且m≠0
即m=3或m=-3
又∵xy<0,∴x,y是异号.
∴m=<0
∴m=3不合题意,舍去.
∴m=-3.
常见错误:忽略m≠0的要求,在解题过程不写这一条件.
4.已知y+b与x+a(a,b是常数)成正比例.
求证:y是x的一次函数.
分析:由y+b与x+a成正比例,设立解析式,分析此解析式为x的一次函数.
解:∵y+b与x+a成正比例
∴可设y+b=k(x+a)(k≠0)
整理,得y=kx+ka-b=kx+(ka-b)
∵k,a,b都是常数.∴ka-b也是常数.
又∵k≠0
∴y是x的一次函数.
常见错误:整理得到y=kx+ka-b时不会把ka-b看作一个整式.
说明:在叙述函数的,一定要说清楚谁是谁的什么名称函数,否则容易发生混淆现象.如本题中,y+b是x+a的正比例这个说法是正确的,同时,y是x的一次函数的说法也是正确的.
七.板书设计
§6.3 一次函数的图象(2)一、如何作一次函数的图象归纳步骤二、做一做(作一次函数的图象)三、议一议(函数y=-2x+5的图象与满足y=-2x+5的x,y所对应的点(x,y)之间的关系)四、课堂练习五、课时小节六、课后作业
6 / 8
