人教版数学七年级下册5.2.2平行线的判定 课件 (共31张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.2.2平行线的判定 课件 (共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 20:31:16 | ||
图片预览











文档简介
(共31张PPT)
5.2.2 平行线的判定
知识点
平行线的判定方法1
感悟新知
1
1. 方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
感悟新知
特别解读:(1)构成同位角的两条直线不一定平行,只有形成的一对同位角相等,这两条直线才平行.
(2)“同位角相等,两直线平行”是通过两个同位角的大小关系(相等)推导出两直线的位置关系(平行). 它是构建起角的大小关系与直线的位置关系的桥梁.
感悟新知
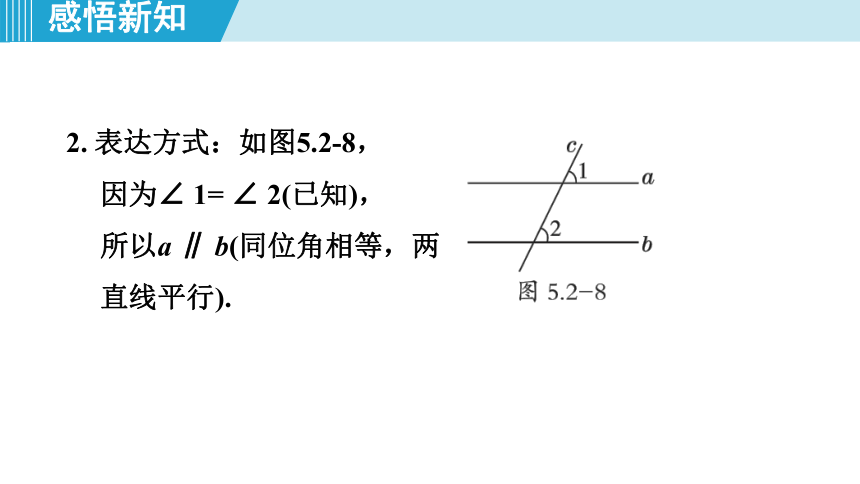
2. 表达方式:如图5.2-8,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(同位角相等,两直线平行).
感悟新知
特别解读
判定两直线平行的方法
●直线的位置关系:
(1) 同一平面内不相交的两条直线平行.
(2) 同平行于第三条直线的两条直线平行.
●角的大小关系:
同位角相等,两直线平行.
感悟新知
如图5.2-9, 已知直线AB,CD 被直线EF 所截,∠ 1+ ∠ 2=180°,AB 与CD 平行吗?请说明理由.
例 1
解题秘方:找出一对同位角,通过已知条件说明这对同位角相等来说明两条直线平行.
感悟新知
解:AB ∥ CD.
理由如下:
因为∠ 1+ ∠ 2=180°,
∠ 2+ ∠ 3=180°,
所以∠ 1= ∠ 3(同角的补角相等).
所以AB ∥ CD(同位角相等,两直线平行).
感悟新知
1-1. 如图,直线a,b 被直线c 所截,下列条件能判断a ∥b 的是( )
A. ∠ 1= ∠ 2
B. ∠ 1= ∠ 4
C. ∠ 3+ ∠ 4=180°
D. ∠ 2=30°,∠ 4=35°
B
知识点
平行线的判定方法2
感悟新知
2
1. 方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
感悟新知
特别解读:(1)“内错角相等,两直线平行”是利用“对顶角相等”和“同位角相等,两直线平行”推导得出的.
(2)利用“内错角相等”来确定“两直线平行”的关键是弄清这对内错角是哪两条直线被第三条直线所截得到的内错角,再说明这两条直线平行.
感悟新知
2. 表达方式:如图5.2-10,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(内错角相等,两直线平行).
感悟新知
特别提醒
构成内错角的两条被截线不一定平行,只有形成的一对内错角相等,这两条被截线才平行.
感悟新知
如图5.2-11,已知∠ ADE=60 °,DF 平分∠ ADE,
∠ 1=30°,试说明DF ∥ BE.
例2
解题秘方:先找出DF 和BE 被DE 所截形成的一对内错角,然后利用条件说明这对内错角相等来说明这两条被截线平行.
感悟新知
解:因为DF 平分∠ ADE(已知),
所以∠ EDF= ∠ ADE(角平分线的定义).
又因为∠ ADE=60° (已知) ,所以∠ EDF=30°.
又因为∠ 1=30° (已知) ,所以∠ EDF= ∠ 1.
所以DF ∥ BE (内错角相等,两直线平行).
感悟新知
2-1. 如图, 已知∠ 1=∠ 2,AC 平分∠ DAB,试说明DC ∥ AB.
解:因为AC平分∠DAB,所以∠1=∠BAC.
因为∠1=∠2,所以∠BAC=∠2,
所以DC∥AB(内错角相等,两直线平行).
知识点
平行线的判定方法3
感悟新知
3
1. 方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
感悟新知
2. 表达方式:如图5.2-12,
因为∠ 1+ ∠ 2=180°(已知),
所以a ∥ b(同旁内角互补,两直线平行).
感悟新知
特别解读
利用同旁内角说明两直线平行时,同旁内角之间的关系是互补,不是相等.
感悟新知
如图5.2-13, 直线AE,CD 相交于点O, 如果
∠ A=110°,∠ 1=70°,就可以说明AB ∥ CD,这是为什么?
例 3
解题秘方:找出AB,CD 被AE 所截形成的同旁内角,利用两个角之间的数量关系来说明这两条直线平行.
感悟新知
解:因为∠ 1= ∠ AOD(对顶角相等),∠ 1=70°,
所以∠ AOD=70°.
又因为∠ A=110°,
所以∠ A+ ∠ AOD=180°.
所以AB ∥ CD(同旁内角互补,两直线平行).
感悟新知
3-1. 如图,(1)由∠ A=∠ 3,可以判定______ ∥ ______ ,根据是_______________________ .
(2)由∠ 2= ∠ E,可以判定______ ∥ ______ ,
根据是_______________________.
(3)由∠ C+ ∠ DBC=180°,可以判定
______ ∥ ______ ,
根据是 __________________________.
AD
BE
同位角相等,两直线平行
BD
CE
内错角相等,两直线平行
BD
CE
同旁内角互补,两直线平行
知识点
平行线判定方法的推论
感悟新知
4
1. 判定方法:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.
简称:在同一平面内,垂直于同
一条直线的两条直线平行.
表达方式:如图5.2-14,直线a,b,c 在同一平面内.
因为a ⊥ b,a ⊥ c,所以b ∥ c.
感悟新知
2. 拓展:
a,b,c 为同一平面内的三条不重合直线,在下列结论中:① a ⊥ b;② a ⊥ c;③ b ∥ c. 已知其中任意两个结论,总能推出第三个结论成立.
感悟新知
特别解读
●三条直线“在同一平面内”是前提,丢掉这个前提,结论不一定成立.
●本结论( 方法) 可看成是判定方法1,2,3 的推论,因为它可由判定方法1,2,3得到.
感悟新知
如图5.2-15,AB ⊥ EF 于B,CD ⊥ EF 于D,
∠ 1= ∠ 2.
(1)请说明AB ∥ CD 的理由;
(2)试问BM 与DN 是否平行?为什么?
解题秘方:根据平行的几种判定方法的模型,从图中找出符合判定的条件,选用合适的方法进行说明.
例4
感悟新知
方法点拨:判定两直线平行的方法
方法一:平行线的定义.
方法二:平行公理的推论.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直线平行.
感悟新知
解:(1)∵ AB ⊥ EF,CD ⊥ EF,
∴ AB ∥ CD(在同一平面内,垂直于同一条直线的两条直线平行).
感悟新知
(2)BM ∥ DN.
理由如下:∵ AB ⊥ EF,CD ⊥ EF,
∴∠ ABE= ∠ CDE=90°.
又∵∠ 1= ∠ 2,
∴∠ ABE-∠ 1= ∠ CDE-∠ 2(等式的性质),
即∠ MBE= ∠ NDE.
∴ BM ∥ DN(同位角相等,两直线平行).
∠ 1 和∠ 2 不是同位角,不能误认为∠ 1和∠ 2 是同位角,直接得出BM ∥ DN,要得到BM ∥ DN,应说明∠ MBE= ∠ NDE.
感悟新知
4-1.[中考·金华] 如图,工人师傅用角尺画出工件边缘AB 的垂线a 和b, 得到a ∥ b, 理由是( )
感悟新知
A. 连接直线外一点与直线上各点的所有线段中,
垂线段最短
B. 在同一平面内,垂直于同一条直线的两条直线互相平行
C. 在同一平面内, 过一点有一条而且仅有一条直线垂直于已知直线
D. 经过直线外一点,有且只有一条直线与这条直线平行
答案:B
课堂小结
平行线的判定
平行线的判定
内错角相等
同位角相等
同旁内角互补
定义
平行公理推论
位置
关系
数量
关系
5.2.2 平行线的判定
知识点
平行线的判定方法1
感悟新知
1
1. 方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
感悟新知
特别解读:(1)构成同位角的两条直线不一定平行,只有形成的一对同位角相等,这两条直线才平行.
(2)“同位角相等,两直线平行”是通过两个同位角的大小关系(相等)推导出两直线的位置关系(平行). 它是构建起角的大小关系与直线的位置关系的桥梁.
感悟新知
2. 表达方式:如图5.2-8,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(同位角相等,两直线平行).
感悟新知
特别解读
判定两直线平行的方法
●直线的位置关系:
(1) 同一平面内不相交的两条直线平行.
(2) 同平行于第三条直线的两条直线平行.
●角的大小关系:
同位角相等,两直线平行.
感悟新知
如图5.2-9, 已知直线AB,CD 被直线EF 所截,∠ 1+ ∠ 2=180°,AB 与CD 平行吗?请说明理由.
例 1
解题秘方:找出一对同位角,通过已知条件说明这对同位角相等来说明两条直线平行.
感悟新知
解:AB ∥ CD.
理由如下:
因为∠ 1+ ∠ 2=180°,
∠ 2+ ∠ 3=180°,
所以∠ 1= ∠ 3(同角的补角相等).
所以AB ∥ CD(同位角相等,两直线平行).
感悟新知
1-1. 如图,直线a,b 被直线c 所截,下列条件能判断a ∥b 的是( )
A. ∠ 1= ∠ 2
B. ∠ 1= ∠ 4
C. ∠ 3+ ∠ 4=180°
D. ∠ 2=30°,∠ 4=35°
B
知识点
平行线的判定方法2
感悟新知
2
1. 方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
感悟新知
特别解读:(1)“内错角相等,两直线平行”是利用“对顶角相等”和“同位角相等,两直线平行”推导得出的.
(2)利用“内错角相等”来确定“两直线平行”的关键是弄清这对内错角是哪两条直线被第三条直线所截得到的内错角,再说明这两条直线平行.
感悟新知
2. 表达方式:如图5.2-10,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(内错角相等,两直线平行).
感悟新知
特别提醒
构成内错角的两条被截线不一定平行,只有形成的一对内错角相等,这两条被截线才平行.
感悟新知
如图5.2-11,已知∠ ADE=60 °,DF 平分∠ ADE,
∠ 1=30°,试说明DF ∥ BE.
例2
解题秘方:先找出DF 和BE 被DE 所截形成的一对内错角,然后利用条件说明这对内错角相等来说明这两条被截线平行.
感悟新知
解:因为DF 平分∠ ADE(已知),
所以∠ EDF= ∠ ADE(角平分线的定义).
又因为∠ ADE=60° (已知) ,所以∠ EDF=30°.
又因为∠ 1=30° (已知) ,所以∠ EDF= ∠ 1.
所以DF ∥ BE (内错角相等,两直线平行).
感悟新知
2-1. 如图, 已知∠ 1=∠ 2,AC 平分∠ DAB,试说明DC ∥ AB.
解:因为AC平分∠DAB,所以∠1=∠BAC.
因为∠1=∠2,所以∠BAC=∠2,
所以DC∥AB(内错角相等,两直线平行).
知识点
平行线的判定方法3
感悟新知
3
1. 方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
感悟新知
2. 表达方式:如图5.2-12,
因为∠ 1+ ∠ 2=180°(已知),
所以a ∥ b(同旁内角互补,两直线平行).
感悟新知
特别解读
利用同旁内角说明两直线平行时,同旁内角之间的关系是互补,不是相等.
感悟新知
如图5.2-13, 直线AE,CD 相交于点O, 如果
∠ A=110°,∠ 1=70°,就可以说明AB ∥ CD,这是为什么?
例 3
解题秘方:找出AB,CD 被AE 所截形成的同旁内角,利用两个角之间的数量关系来说明这两条直线平行.
感悟新知
解:因为∠ 1= ∠ AOD(对顶角相等),∠ 1=70°,
所以∠ AOD=70°.
又因为∠ A=110°,
所以∠ A+ ∠ AOD=180°.
所以AB ∥ CD(同旁内角互补,两直线平行).
感悟新知
3-1. 如图,(1)由∠ A=∠ 3,可以判定______ ∥ ______ ,根据是_______________________ .
(2)由∠ 2= ∠ E,可以判定______ ∥ ______ ,
根据是_______________________.
(3)由∠ C+ ∠ DBC=180°,可以判定
______ ∥ ______ ,
根据是 __________________________.
AD
BE
同位角相等,两直线平行
BD
CE
内错角相等,两直线平行
BD
CE
同旁内角互补,两直线平行
知识点
平行线判定方法的推论
感悟新知
4
1. 判定方法:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.
简称:在同一平面内,垂直于同
一条直线的两条直线平行.
表达方式:如图5.2-14,直线a,b,c 在同一平面内.
因为a ⊥ b,a ⊥ c,所以b ∥ c.
感悟新知
2. 拓展:
a,b,c 为同一平面内的三条不重合直线,在下列结论中:① a ⊥ b;② a ⊥ c;③ b ∥ c. 已知其中任意两个结论,总能推出第三个结论成立.
感悟新知
特别解读
●三条直线“在同一平面内”是前提,丢掉这个前提,结论不一定成立.
●本结论( 方法) 可看成是判定方法1,2,3 的推论,因为它可由判定方法1,2,3得到.
感悟新知
如图5.2-15,AB ⊥ EF 于B,CD ⊥ EF 于D,
∠ 1= ∠ 2.
(1)请说明AB ∥ CD 的理由;
(2)试问BM 与DN 是否平行?为什么?
解题秘方:根据平行的几种判定方法的模型,从图中找出符合判定的条件,选用合适的方法进行说明.
例4
感悟新知
方法点拨:判定两直线平行的方法
方法一:平行线的定义.
方法二:平行公理的推论.
方法三:同位角相等,两直线平行.
方法四:内错角相等,两直线平行.
方法五:同旁内角互补,两直线平行.
方法六:在同一平面内,垂直于同一条直线的两条直线平行.
感悟新知
解:(1)∵ AB ⊥ EF,CD ⊥ EF,
∴ AB ∥ CD(在同一平面内,垂直于同一条直线的两条直线平行).
感悟新知
(2)BM ∥ DN.
理由如下:∵ AB ⊥ EF,CD ⊥ EF,
∴∠ ABE= ∠ CDE=90°.
又∵∠ 1= ∠ 2,
∴∠ ABE-∠ 1= ∠ CDE-∠ 2(等式的性质),
即∠ MBE= ∠ NDE.
∴ BM ∥ DN(同位角相等,两直线平行).
∠ 1 和∠ 2 不是同位角,不能误认为∠ 1和∠ 2 是同位角,直接得出BM ∥ DN,要得到BM ∥ DN,应说明∠ MBE= ∠ NDE.
感悟新知
4-1.[中考·金华] 如图,工人师傅用角尺画出工件边缘AB 的垂线a 和b, 得到a ∥ b, 理由是( )
感悟新知
A. 连接直线外一点与直线上各点的所有线段中,
垂线段最短
B. 在同一平面内,垂直于同一条直线的两条直线互相平行
C. 在同一平面内, 过一点有一条而且仅有一条直线垂直于已知直线
D. 经过直线外一点,有且只有一条直线与这条直线平行
答案:B
课堂小结
平行线的判定
平行线的判定
内错角相等
同位角相等
同旁内角互补
定义
平行公理推论
位置
关系
数量
关系
