人教版数学七年级下册5.3.1平行线的性质 课件 (共18张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.3.1平行线的性质 课件 (共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 20:33:53 | ||
图片预览






文档简介
(共18张PPT)
5.3.1 平行线的性质
知识点
平行线的性质1
感悟新知
1
1. 性质1:两条平行线被第三条直线所截,同位角相等 .
简单说成:两直线平行,同位角相等.
表达方式:如图5.3-1,因为a ∥ b(已知),
所以∠ 1= ∠ 2(两直线平行,同位角相等).
感悟新知
2. 平行线的性质与平行线的判定的区别:
(1)平行线的判定是根据两角的数量关系得到两条直线的位置关系,而平行线的性质是根据两条直线的位置关系得到两角的数量关系;
(2)平行线的判定的条件是平行线的性质的结论,而平行线的判定的结论是平行线的性质的条件.
感悟新知
特别警示
●两条直线平行是前提,只有在这个前提下才有同位角相等;
●格式书写时,顺序不能颠倒,与判定不能混淆.
感悟新知
如图5.3-2,把三角尺的直角顶点放在直尺的一边上,
若∠ 1=30°,则∠ 2 的度数为( )
A.60°
B.50°
C.40°
D.30°
例 1
A
感悟新知
解:∵∠ 1+ ∠ BAC+ ∠ DAB=180°,
∠ BAC=90°,∠ 1=30°,
∴∠ DAB=180°-∠ 1-∠ BAC=60°.
∵直尺的对边平行,即EF ∥ AD,
∴ ∠ 2= ∠ DAB=60°.
解题秘方:根据直尺的对边平行,利用平行线的性质建立已知角∠ 1 与待求的角∠ 2 之间的数量关系.
感悟新知
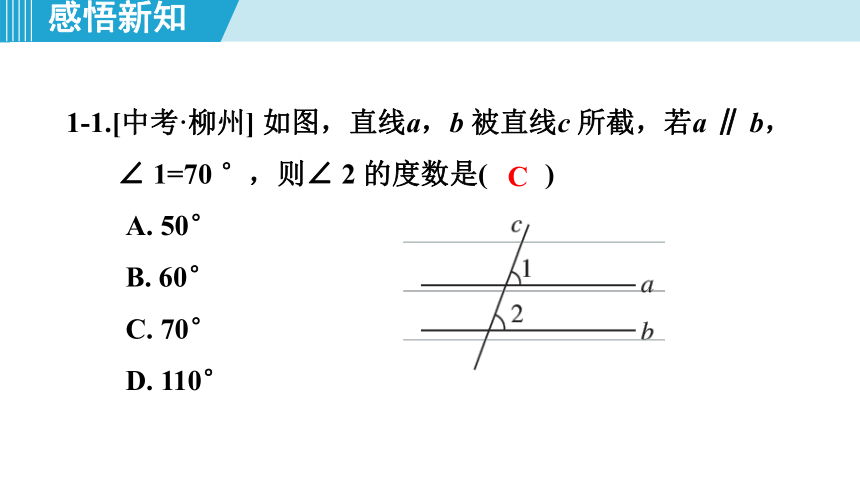
1-1.[中考·柳州] 如图,直线a,b 被直线c 所截,若a ∥ b, ∠ 1=70 °,则∠ 2 的度数是( )
A. 50°
B. 60°
C. 70°
D. 110°
C
知识点
平行线的性质2
感悟新知
2
1. 性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
2. 表达方式:如图5.3-3,因为a ∥ b(已知),
所以∠ 1= ∠ 2(两直线平行,内错角相等).
感悟新知
特别警示
并不是所有的内错角都相等,只有在“两直线平行”的前提下,才有内错角相等.
感悟新知
如图5.3-4,AB ∥ CD,BE 平分∠ ABC,CF 平分
∠ BCD,你能发现BE 和CF 有何特殊的位置关系吗?说说你的理由.
例2
解题秘方:由两直线平行得到内错角相等,再由内错角相等得到两直线平行.
感悟新知
解:BE∥CF.理由如下:∵ AB∥CD(已知),
∴∠ ABC= ∠ BCD (两直线平行,内错角相等).
∵ BE 平分∠ ABC,CF 平分∠ BCD (已知),
∴∠ 2= ∠ ABC,∠ 1= ∠ BCD (角平分线的定义).
∴∠ 2= ∠ 1. ∴ BE ∥ CF (内错角相等,两直线平行).
感悟新知
2-1. 如图,已知AB ∥CD,∠ ADC= ∠ ABC.
试说明∠ E= ∠ F.
解:∵AB∥CD,
∴∠ABC=∠DCF.
又∵∠ADC=∠ABC,
∴∠ADC=∠DCF,
∴DE∥BF.∴∠E=∠F.
知识点
平行线的性质3
感悟新知
3
1. 性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
2. 表达方式:如图5.3-5,
因为a ∥ b(已知),
所以∠ 1+ ∠ 2=180° (两直线平行,同旁内角互补).
感悟新知
警示误区
两直线平行时,同旁内角是互补的关系而不是相等的关系
感悟新知
[中考·黄冈] 已知:如图5.3-6,直线a ∥ b,∠ 1=
50°,∠ 2= ∠ 3,则∠ 2 的度数为( )
A.50°
B.60°
C.65°
D.75°
例 3
C
感悟新知
解题秘方:由平行线的性质找出∠ 1 与∠ 2和∠ 3 之间的数量关系,利用∠ 1 的度数求出∠ 2 的度数.
解:∵ a ∥ b, ∴∠ 1+ ∠ 2+ ∠ 3=180°.
又∵∠ 1=50°,∴∠ 2+ ∠ 3=130°. ∴∠ 2=65°.
感悟新知
3-1.[中考·西藏] 如图,l1 ∥l2,∠ 1=38°,∠ 2=46 °, 则∠ 3 的度数为( )
A. 46°
B. 90°
C. 96°
D. 134°
C
课堂小结
平行线的性质
平行线的性质
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
5.3.1 平行线的性质
知识点
平行线的性质1
感悟新知
1
1. 性质1:两条平行线被第三条直线所截,同位角相等 .
简单说成:两直线平行,同位角相等.
表达方式:如图5.3-1,因为a ∥ b(已知),
所以∠ 1= ∠ 2(两直线平行,同位角相等).
感悟新知
2. 平行线的性质与平行线的判定的区别:
(1)平行线的判定是根据两角的数量关系得到两条直线的位置关系,而平行线的性质是根据两条直线的位置关系得到两角的数量关系;
(2)平行线的判定的条件是平行线的性质的结论,而平行线的判定的结论是平行线的性质的条件.
感悟新知
特别警示
●两条直线平行是前提,只有在这个前提下才有同位角相等;
●格式书写时,顺序不能颠倒,与判定不能混淆.
感悟新知
如图5.3-2,把三角尺的直角顶点放在直尺的一边上,
若∠ 1=30°,则∠ 2 的度数为( )
A.60°
B.50°
C.40°
D.30°
例 1
A
感悟新知
解:∵∠ 1+ ∠ BAC+ ∠ DAB=180°,
∠ BAC=90°,∠ 1=30°,
∴∠ DAB=180°-∠ 1-∠ BAC=60°.
∵直尺的对边平行,即EF ∥ AD,
∴ ∠ 2= ∠ DAB=60°.
解题秘方:根据直尺的对边平行,利用平行线的性质建立已知角∠ 1 与待求的角∠ 2 之间的数量关系.
感悟新知
1-1.[中考·柳州] 如图,直线a,b 被直线c 所截,若a ∥ b, ∠ 1=70 °,则∠ 2 的度数是( )
A. 50°
B. 60°
C. 70°
D. 110°
C
知识点
平行线的性质2
感悟新知
2
1. 性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
2. 表达方式:如图5.3-3,因为a ∥ b(已知),
所以∠ 1= ∠ 2(两直线平行,内错角相等).
感悟新知
特别警示
并不是所有的内错角都相等,只有在“两直线平行”的前提下,才有内错角相等.
感悟新知
如图5.3-4,AB ∥ CD,BE 平分∠ ABC,CF 平分
∠ BCD,你能发现BE 和CF 有何特殊的位置关系吗?说说你的理由.
例2
解题秘方:由两直线平行得到内错角相等,再由内错角相等得到两直线平行.
感悟新知
解:BE∥CF.理由如下:∵ AB∥CD(已知),
∴∠ ABC= ∠ BCD (两直线平行,内错角相等).
∵ BE 平分∠ ABC,CF 平分∠ BCD (已知),
∴∠ 2= ∠ ABC,∠ 1= ∠ BCD (角平分线的定义).
∴∠ 2= ∠ 1. ∴ BE ∥ CF (内错角相等,两直线平行).
感悟新知
2-1. 如图,已知AB ∥CD,∠ ADC= ∠ ABC.
试说明∠ E= ∠ F.
解:∵AB∥CD,
∴∠ABC=∠DCF.
又∵∠ADC=∠ABC,
∴∠ADC=∠DCF,
∴DE∥BF.∴∠E=∠F.
知识点
平行线的性质3
感悟新知
3
1. 性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
2. 表达方式:如图5.3-5,
因为a ∥ b(已知),
所以∠ 1+ ∠ 2=180° (两直线平行,同旁内角互补).
感悟新知
警示误区
两直线平行时,同旁内角是互补的关系而不是相等的关系
感悟新知
[中考·黄冈] 已知:如图5.3-6,直线a ∥ b,∠ 1=
50°,∠ 2= ∠ 3,则∠ 2 的度数为( )
A.50°
B.60°
C.65°
D.75°
例 3
C
感悟新知
解题秘方:由平行线的性质找出∠ 1 与∠ 2和∠ 3 之间的数量关系,利用∠ 1 的度数求出∠ 2 的度数.
解:∵ a ∥ b, ∴∠ 1+ ∠ 2+ ∠ 3=180°.
又∵∠ 1=50°,∴∠ 2+ ∠ 3=130°. ∴∠ 2=65°.
感悟新知
3-1.[中考·西藏] 如图,l1 ∥l2,∠ 1=38°,∠ 2=46 °, 则∠ 3 的度数为( )
A. 46°
B. 90°
C. 96°
D. 134°
C
课堂小结
平行线的性质
平行线的性质
两直线平行
条件
结论
同位角相等
内错角相等
同旁内角互补
