数学人教A版(2019)选择性必修第二册4.3.2 等比数列的前n项和公式(共24张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第二册4.3.2 等比数列的前n项和公式(共24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 971.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 09:04:23 | ||
图片预览








文档简介
(共24张PPT)
第四章 数列
4.3.2. 等比数列的前n项和公式
等差数列 等比数列
定义 an - an-1=d
公差 d 可以是0 q不可以是0
等差中项 2A=a+b G2=ab
通项公式 an=a1+(n-1)d an=an=am+(n-m)d an=a1qn-1
an=amqn-m
性质(若m+n=p+q=2k) ap + aq = as + at= 2ak ap aq = as at=
复习引入
数学小故事:国际象棋起源于古印度.棋盘上共有8行8列构成64个格子.传说国王要奖赏国际象棋的发明者,问他有什么要求,发明者说:“请在棋盘的第1个格子里放上1颗麦粒,在棋盘的第2个格子里放上2颗麦粒,在棋盘的第3个格子里放上4颗麦粒,在棋盘的第4个格子里放上8颗麦粒,以此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的粮食来实现上述要求.”
1
2
2
3
3
4
4
5
5
1
6
6
7
7
8
8
你想得到
什么样的
赏赐?
陛下,赏小
人一些麦粒就可以.
请在第一个格
子放1颗麦粒
请在第二个格
子放2颗麦粒
请在第三个格
子放4颗麦粒
请在第四个格
子放8颗麦粒
依次类推……
新课引入
就在国王犹豫是否要答应发明者的要求时,站在一旁一位将告老还乡的大臣听后不满地说:“我跟陛下这么多年战功卓著,请求陛下同样赏赐给我麦子,在棋盘的第一格子里放上2颗麦粒,在第2个格子里放上4颗麦粒,在第3个格子里放上8颗麦粒,依次类推,每一个格子放的麦粒数都是前一个格子里放的麦粒数的2倍,直到放完64个格子为止.”
国王觉得这个要求不高,就欣然同意了.
思考:已知一千颗麦粒的质量约为40g,据查,2016-2017年度世界小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他们的诺言.
新课引入
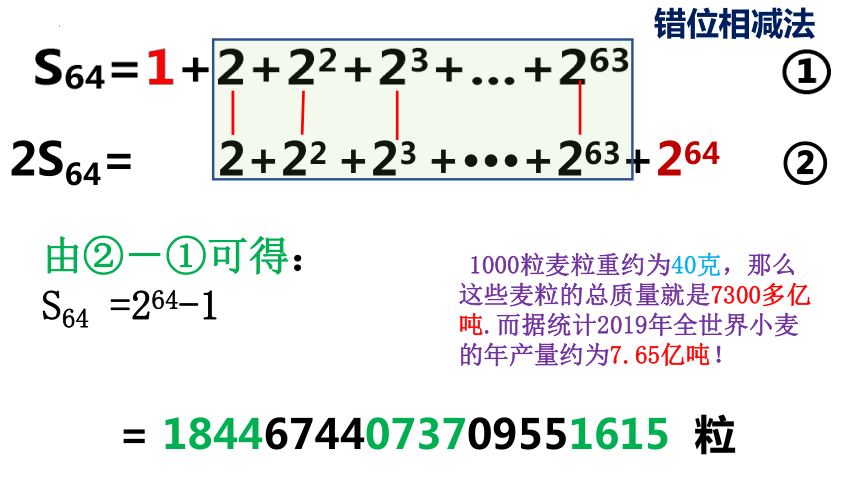
2S64= 2+22 +23 +···+263+264 ②
由②-①可得:
S64 =264-1
= 18446744073709551615 粒
错位相减法
1000粒麦粒重约为40克,那么这些麦粒的总质量就是7300多亿吨.而据统计2019年全世界小麦的年产量约为7.65亿吨!
如何计算等比数列的前n项和?
已知等比数列首项为,公比为q,则
两边同乘q:
①
②
(1 – q)Sn = a1 – a1qn
由①-②得:
当q=1时,
这种求和方法称为
错位相减法
当q≠1时,
步骤: 乘公比,错位写,正位减
设等比数列{} 的首项为,公比为q,数列{} 的前
当q=1时,
当q≠1时,
因为=,所以公式也可以写成
思考:运用公式求和,需注意什么问题?
若已知 , q,套用
(2)当q≠1时,若已知 , q,n套用;
课堂探究
步骤: 乘公比,错位写,正位减
n个
判断下列计算是否正确
公式巩固
解: 将该等比数列记作{an},公比为q,则
因此
例 1. 求等比数列 的各项的和.
想一想
在等比数列 {an} 中,若已知五个量
a1, an, n, q, Sn 中的任意三个量,
请问: 能否求出其余两个量
方程思想,
知 三 求 二
例2.已知等比数列
中,
,
求
①
②
解:
得
则
在等比数列{an}的五个量a1,q,an,n,Sn中,a1与q是最基本的元素,当条件与结论间的联系不明显时,均可以用a1与q表示an与Sn,从而列方程组求解,在解方程组时经常用到两式相除达到整体消元的目的.这是方程思想与整体思想在数列中的具体应用.
例3
练习.在等比数列{an}中,若
Sn=189,q=2,an=96,求a1和n;
∴a1=3.
n=6.
Sn=189,
an=96,
例4. 在等比数列{an}中,若a1+a3=10,a4+a6= ,求a4和S5;
∴a1=8.
∵a1≠0,1+q2≠0,
( )
( )
( )
错位相减法步骤:乘公比,错位写,正位减
等差数列
等比数列
.
例5
等比数列的前项和n公式:
如果等比数列{an}的首项a1,公比为q,那么该等比数列的前n项和公式为:
等比数列的通项公式和前n项和公式中,共有“a1,q ,n,an,Sn”五个量,
故知三可求其二.(注意方程思想的应用)
错位相减法步骤:
乘公比,错位写,正位减
等差数列
等比数列
.
练习巩固
练习巩固
练习巩固
②-①,得
3
累加法
方法拓展1
提取公比法
方法拓展2
即
n为奇数,q为-1时此法不适用
方法拓展3
利用等比定理
设等比数列{} 的首项为,公比为q,数列{} 的前
当q=1时,
当q≠1时,
因为=,所以公式也可以写成
思考:运用公式求和,需注意什么问题?
若已知 , q,套用
(2)当q≠1时,若已知 , q,n套用;
步骤: 乘公比,错位写,正位减
课堂小结
第四章 数列
4.3.2. 等比数列的前n项和公式
等差数列 等比数列
定义 an - an-1=d
公差 d 可以是0 q不可以是0
等差中项 2A=a+b G2=ab
通项公式 an=a1+(n-1)d an=an=am+(n-m)d an=a1qn-1
an=amqn-m
性质(若m+n=p+q=2k) ap + aq = as + at= 2ak ap aq = as at=
复习引入
数学小故事:国际象棋起源于古印度.棋盘上共有8行8列构成64个格子.传说国王要奖赏国际象棋的发明者,问他有什么要求,发明者说:“请在棋盘的第1个格子里放上1颗麦粒,在棋盘的第2个格子里放上2颗麦粒,在棋盘的第3个格子里放上4颗麦粒,在棋盘的第4个格子里放上8颗麦粒,以此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的粮食来实现上述要求.”
1
2
2
3
3
4
4
5
5
1
6
6
7
7
8
8
你想得到
什么样的
赏赐?
陛下,赏小
人一些麦粒就可以.
请在第一个格
子放1颗麦粒
请在第二个格
子放2颗麦粒
请在第三个格
子放4颗麦粒
请在第四个格
子放8颗麦粒
依次类推……
新课引入
就在国王犹豫是否要答应发明者的要求时,站在一旁一位将告老还乡的大臣听后不满地说:“我跟陛下这么多年战功卓著,请求陛下同样赏赐给我麦子,在棋盘的第一格子里放上2颗麦粒,在第2个格子里放上4颗麦粒,在第3个格子里放上8颗麦粒,依次类推,每一个格子放的麦粒数都是前一个格子里放的麦粒数的2倍,直到放完64个格子为止.”
国王觉得这个要求不高,就欣然同意了.
思考:已知一千颗麦粒的质量约为40g,据查,2016-2017年度世界小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他们的诺言.
新课引入
2S64= 2+22 +23 +···+263+264 ②
由②-①可得:
S64 =264-1
= 18446744073709551615 粒
错位相减法
1000粒麦粒重约为40克,那么这些麦粒的总质量就是7300多亿吨.而据统计2019年全世界小麦的年产量约为7.65亿吨!
如何计算等比数列的前n项和?
已知等比数列首项为,公比为q,则
两边同乘q:
①
②
(1 – q)Sn = a1 – a1qn
由①-②得:
当q=1时,
这种求和方法称为
错位相减法
当q≠1时,
步骤: 乘公比,错位写,正位减
设等比数列{} 的首项为,公比为q,数列{} 的前
当q=1时,
当q≠1时,
因为=,所以公式也可以写成
思考:运用公式求和,需注意什么问题?
若已知 , q,套用
(2)当q≠1时,若已知 , q,n套用;
课堂探究
步骤: 乘公比,错位写,正位减
n个
判断下列计算是否正确
公式巩固
解: 将该等比数列记作{an},公比为q,则
因此
例 1. 求等比数列 的各项的和.
想一想
在等比数列 {an} 中,若已知五个量
a1, an, n, q, Sn 中的任意三个量,
请问: 能否求出其余两个量
方程思想,
知 三 求 二
例2.已知等比数列
中,
,
求
①
②
解:
得
则
在等比数列{an}的五个量a1,q,an,n,Sn中,a1与q是最基本的元素,当条件与结论间的联系不明显时,均可以用a1与q表示an与Sn,从而列方程组求解,在解方程组时经常用到两式相除达到整体消元的目的.这是方程思想与整体思想在数列中的具体应用.
例3
练习.在等比数列{an}中,若
Sn=189,q=2,an=96,求a1和n;
∴a1=3.
n=6.
Sn=189,
an=96,
例4. 在等比数列{an}中,若a1+a3=10,a4+a6= ,求a4和S5;
∴a1=8.
∵a1≠0,1+q2≠0,
( )
( )
( )
错位相减法步骤:乘公比,错位写,正位减
等差数列
等比数列
.
例5
等比数列的前项和n公式:
如果等比数列{an}的首项a1,公比为q,那么该等比数列的前n项和公式为:
等比数列的通项公式和前n项和公式中,共有“a1,q ,n,an,Sn”五个量,
故知三可求其二.(注意方程思想的应用)
错位相减法步骤:
乘公比,错位写,正位减
等差数列
等比数列
.
练习巩固
练习巩固
练习巩固
②-①,得
3
累加法
方法拓展1
提取公比法
方法拓展2
即
n为奇数,q为-1时此法不适用
方法拓展3
利用等比定理
设等比数列{} 的首项为,公比为q,数列{} 的前
当q=1时,
当q≠1时,
因为=,所以公式也可以写成
思考:运用公式求和,需注意什么问题?
若已知 , q,套用
(2)当q≠1时,若已知 , q,n套用;
步骤: 乘公比,错位写,正位减
课堂小结
