第五章 投影与视图单元练习题(含答案)
文档属性
| 名称 | 第五章 投影与视图单元练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 838.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-19 22:04:13 | ||
图片预览



文档简介
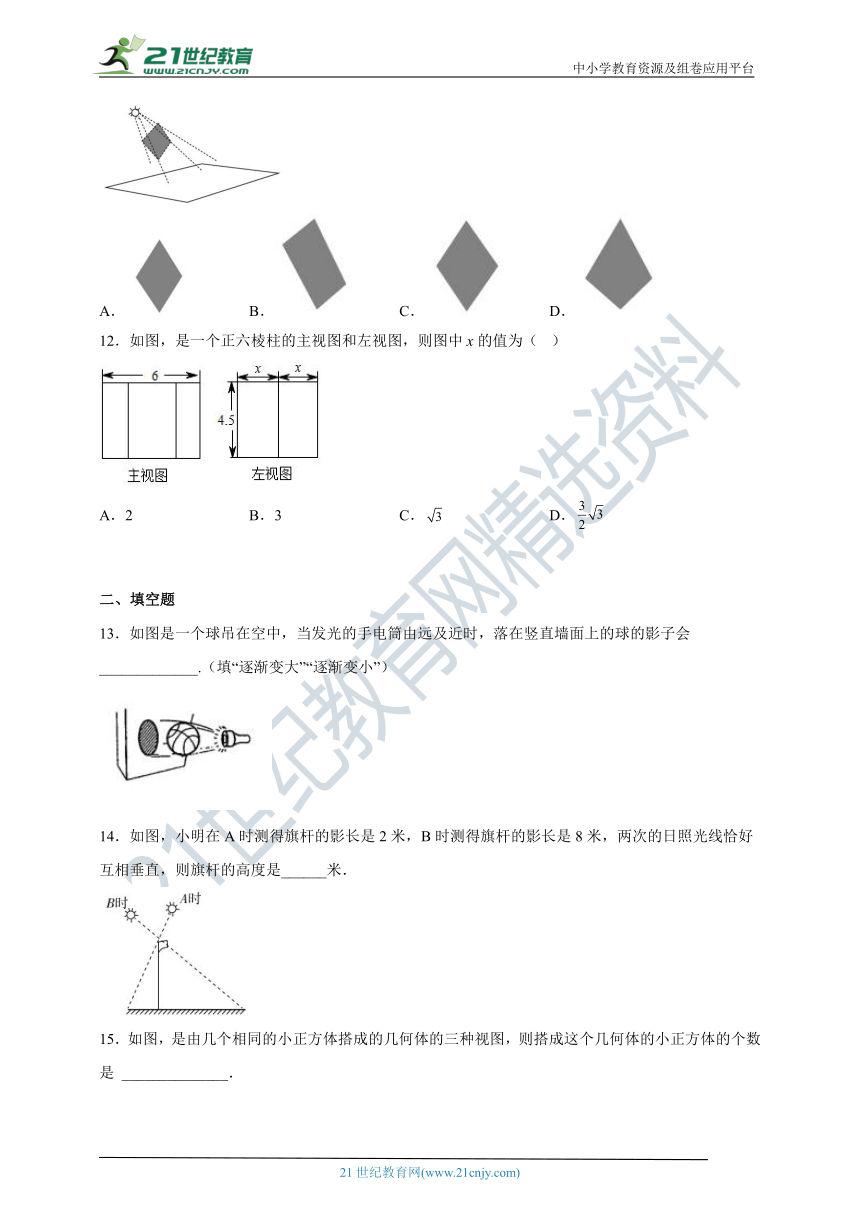
中小学教育资源及组卷应用平台
北师大版九年级数学上册第五章《投影与视图》单元练习题(含答案)
一、单选题
1.一个画家有14个边长为1米的正方体,他在地面上把它们摆成如图所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )平方米.
A.19 B.21 C.33 D.36
2.晚上,人在马路上走过一盏路灯的过程中,其影子长度的变化情况是( )
A.先变短后变长 B.先变长后变短 C.逐渐变短 D.逐渐变长
3.如图是一根电线杆在一天中不同时刻的影长图,试按其天中发生的先后顺序排列,正确的是( )
A.①②③④ B.④①③② C.④②③① D.④③②①
4.三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A. B. C. D.
5.下列各种现象属于中心投影的是( )
A.晚上人走在路灯下的影子 B.中午用来乘凉的树影
C.上午人走在路上的影子 D.阳光下旗杆的影子
6.几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A.3 B.4 C.6 D.9
7.在同一时刻,将两根长度不等的竹竿置于阳光之下,但它们的影长相等,那么这两根竹竿的相对位置是( )
A.两根竹竿都垂直于地面 B.以两根竹竿平行斜插在地上
C.两根竹竿不平行 D.无法确定
8.下列立体图形中,主视图是圆的是( )
A. B. C. D.
9.图1、图2均是正方体,图3是由一些大小相同的正方体搭成的几何体从正面看和左面看得到的形状图,小敏同学经过研究得到如下结论:
(1)若将图1中正方体的表面沿某些棱剪开,展成一个平面图形,需要剪开7条棱;
(2)用一个平面从不同方向去截图1中的正方体,得到的截面可能是三角形、四边形、五边形或六边形;
(3)用一个平面去截图1中的正方体得到图2,截面三角形ABC中∠ABC=45°;
(4)如图3,要搭成该几何体的正方体的个数最少是a,最多是b,则a+b=19
其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图所示是两根标杆在地面上的影子,根据这些投影,在灯光下形成的影子是( )
A.①和② B.②和④ C.③和④ D.②和③
11.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A. B. C. D.
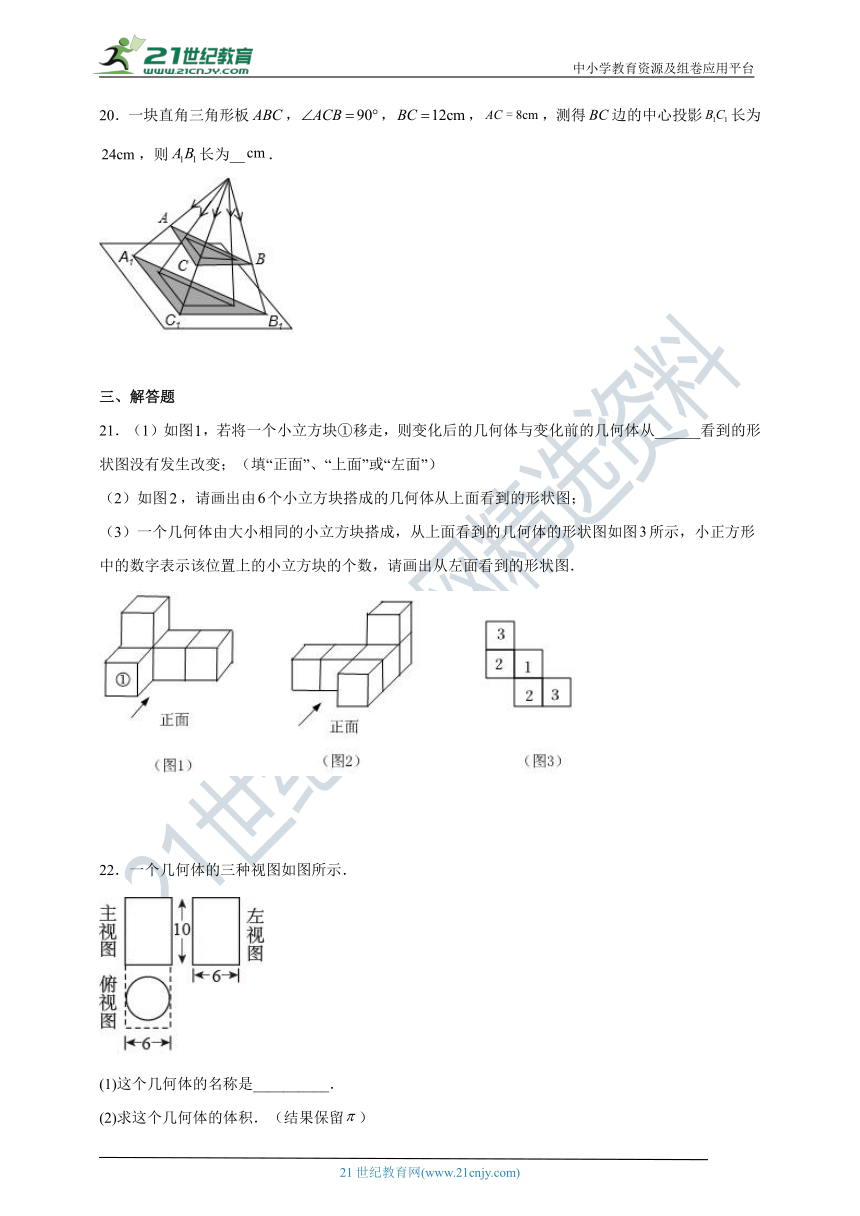
12.如图,是一个正六棱柱的主视图和左视图,则图中x的值为( )
A.2 B.3 C. D.
二、填空题
13.如图是一个球吊在空中,当发光的手电筒由远及近时,落在竖直墙面上的球的影子会_____________.(填“逐渐变大”“逐渐变小”)
14.如图,小明在A时测得旗杆的影长是2米,B时测得旗杆的影长是8米,两次的日照光线恰好互相垂直,则旗杆的高度是______米.
15.如图,是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是 ______________.
16.一个几何体的三视图如图所示,则该几何体的表面积为____________.
17.在同车道行驶的机动车,后车应当与前车保持一定的安全距离.如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m处,小林驾驶一辆小轿车,距大车尾xm,若大巴车车顶高于小林的水平视线0.8m,红灯下沿高于小林的水平视线3.2m,若小林能看到整个红灯,则x的最小值为_____.
18.如图,在A时测得一棵大树的影长为4米,B时又测得该树的影长为6米,若两次日照的光线互相垂直,则树的高度是______.
19.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要______个小立方块.
20.一块直角三角形板,,,,测得边的中心投影长为,则长为__.
三、解答题
21.(1)如图,若将一个小立方块①移走,则变化后的几何体与变化前的几何体从______看到的形状图没有发生改变;(填“正面”、“上面”或“左面”)
(2)如图,请画出由个小立方块搭成的几何体从上面看到的形状图;
(3)一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,小正方形中的数字表示该位置上的小立方块的个数,请画出从左面看到的形状图.
22.一个几何体的三种视图如图所示.
(1)这个几何体的名称是__________.
(2)求这个几何体的体积.(结果保留)
23.如图,九(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竿AB的长为3m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2m.
(1)请你在图中画出此时旗杆DE在阳光下的投影;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6m,请你计算旗杆DE的高度.
24.如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在太阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,计算DE的长
25.如图,身高为的小王晚上沿箭头的方向散步至一路灯下,她想通过自己的影子来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到处,发现自己影子端点恰好在点处,继续沿刚才自己的影子走5步到处,此时影子的端点在处.
(1)找出路灯的位置;
(2)估计路灯的高度,并求影长.
26.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=5m,求围墙AB的高度.
27.小明在晚上由路灯走向路灯,当他走到处时,发现身后影子顶部正好触到路灯底部,当他向前再步行到达时,发现他的影子的顶点正好接触到路灯的底部.已知小明的身高是,两个路灯的高度都是,且.
(1)求:两个路灯之间的距离;
(2)小明在两个路灯之间行走时,在两个路灯下的影长之和是否为定值?如果是定值,直接写出此定值,如果不是定值,求说明理由。
参考答案
1.C2.A3.B4.B5.A6.B7.B8.D9.B10.D11.D12.D
13.逐渐变大
14.4
15.4
16.3π+4
17.10m
18.6
19.26
20.
21.解:(1)如图1,将一个正方体①移走后,变化后的几何体与变化前的几何体从正面看到的形状图相同.
故答案为:正面;
(2)如图所示:
(3)如图所示:
22.(1)解:由该几何体的三视图,可得这个几何体是圆柱.
故答案为:圆柱.
(2)
解:由该几何体的三视图可知:该圆柱的高为10,底面直径为6,
∴这个几何体的体积为:.
23.解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影,如图所示:
(2)∵DF∥AC,
∴∠ACB=∠DFE,
∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF,
∴,
∵AB=3m,BC=2m,EF=6m,
∴,
∴DE=9m;
答:旗杆DE的高度为9m.
24.(1)解:DE在阳光下的投影是EF如图所示;
(2)
在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,
∵△ABC∽△DEF,AB=5m,BC=3m,EF=6m,
∴,
∴,
∴DE=10(m),
答:DE的长为10m.
25.(1)如图,点为路灯的位置;
(2)作垂直地面,如图,0步,步,,
∵,
∴,
∴,即,解得,
∵,
∴,
∴,即,
解得.
答:路灯的高,影长为步.
26.解:延长OD,
∵DO⊥BF,
∴∠DOE=90°,
∵OD=1m,OE=1m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=x m,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴,
,
解得:x=4.
经检验:x=4是原方程的解.
答:围墙AB的高度是4m.
27.(1)解:由题意得,
∵,
∴∽,
则
解得:,
,
故两路灯之间的距离为米;
(2)
解:两影长之和为定值,定值为米.
理由:如图,设米.
∵,
∴△CPK∽△EAK,△CPQ∽△HBQ,
∴,,
则,,
∵
∴,
,
解得,
两影长之和为定值,定值为米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版九年级数学上册第五章《投影与视图》单元练习题(含答案)
一、单选题
1.一个画家有14个边长为1米的正方体,他在地面上把它们摆成如图所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )平方米.
A.19 B.21 C.33 D.36
2.晚上,人在马路上走过一盏路灯的过程中,其影子长度的变化情况是( )
A.先变短后变长 B.先变长后变短 C.逐渐变短 D.逐渐变长
3.如图是一根电线杆在一天中不同时刻的影长图,试按其天中发生的先后顺序排列,正确的是( )
A.①②③④ B.④①③② C.④②③① D.④③②①
4.三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A. B. C. D.
5.下列各种现象属于中心投影的是( )
A.晚上人走在路灯下的影子 B.中午用来乘凉的树影
C.上午人走在路上的影子 D.阳光下旗杆的影子
6.几个大小相同,且棱长为1的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
A.3 B.4 C.6 D.9
7.在同一时刻,将两根长度不等的竹竿置于阳光之下,但它们的影长相等,那么这两根竹竿的相对位置是( )
A.两根竹竿都垂直于地面 B.以两根竹竿平行斜插在地上
C.两根竹竿不平行 D.无法确定
8.下列立体图形中,主视图是圆的是( )
A. B. C. D.
9.图1、图2均是正方体,图3是由一些大小相同的正方体搭成的几何体从正面看和左面看得到的形状图,小敏同学经过研究得到如下结论:
(1)若将图1中正方体的表面沿某些棱剪开,展成一个平面图形,需要剪开7条棱;
(2)用一个平面从不同方向去截图1中的正方体,得到的截面可能是三角形、四边形、五边形或六边形;
(3)用一个平面去截图1中的正方体得到图2,截面三角形ABC中∠ABC=45°;
(4)如图3,要搭成该几何体的正方体的个数最少是a,最多是b,则a+b=19
其中正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图所示是两根标杆在地面上的影子,根据这些投影,在灯光下形成的影子是( )
A.①和② B.②和④ C.③和④ D.②和③
11.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A. B. C. D.
12.如图,是一个正六棱柱的主视图和左视图,则图中x的值为( )
A.2 B.3 C. D.
二、填空题
13.如图是一个球吊在空中,当发光的手电筒由远及近时,落在竖直墙面上的球的影子会_____________.(填“逐渐变大”“逐渐变小”)
14.如图,小明在A时测得旗杆的影长是2米,B时测得旗杆的影长是8米,两次的日照光线恰好互相垂直,则旗杆的高度是______米.
15.如图,是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是 ______________.
16.一个几何体的三视图如图所示,则该几何体的表面积为____________.
17.在同车道行驶的机动车,后车应当与前车保持一定的安全距离.如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m处,小林驾驶一辆小轿车,距大车尾xm,若大巴车车顶高于小林的水平视线0.8m,红灯下沿高于小林的水平视线3.2m,若小林能看到整个红灯,则x的最小值为_____.
18.如图,在A时测得一棵大树的影长为4米,B时又测得该树的影长为6米,若两次日照的光线互相垂直,则树的高度是______.
19.如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要______个小立方块.
20.一块直角三角形板,,,,测得边的中心投影长为,则长为__.
三、解答题
21.(1)如图,若将一个小立方块①移走,则变化后的几何体与变化前的几何体从______看到的形状图没有发生改变;(填“正面”、“上面”或“左面”)
(2)如图,请画出由个小立方块搭成的几何体从上面看到的形状图;
(3)一个几何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,小正方形中的数字表示该位置上的小立方块的个数,请画出从左面看到的形状图.
22.一个几何体的三种视图如图所示.
(1)这个几何体的名称是__________.
(2)求这个几何体的体积.(结果保留)
23.如图,九(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竿AB的长为3m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2m.
(1)请你在图中画出此时旗杆DE在阳光下的投影;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6m,请你计算旗杆DE的高度.
24.如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在太阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,计算DE的长
25.如图,身高为的小王晚上沿箭头的方向散步至一路灯下,她想通过自己的影子来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到处,发现自己影子端点恰好在点处,继续沿刚才自己的影子走5步到处,此时影子的端点在处.
(1)找出路灯的位置;
(2)估计路灯的高度,并求影长.
26.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=5m,求围墙AB的高度.
27.小明在晚上由路灯走向路灯,当他走到处时,发现身后影子顶部正好触到路灯底部,当他向前再步行到达时,发现他的影子的顶点正好接触到路灯的底部.已知小明的身高是,两个路灯的高度都是,且.
(1)求:两个路灯之间的距离;
(2)小明在两个路灯之间行走时,在两个路灯下的影长之和是否为定值?如果是定值,直接写出此定值,如果不是定值,求说明理由。
参考答案
1.C2.A3.B4.B5.A6.B7.B8.D9.B10.D11.D12.D
13.逐渐变大
14.4
15.4
16.3π+4
17.10m
18.6
19.26
20.
21.解:(1)如图1,将一个正方体①移走后,变化后的几何体与变化前的几何体从正面看到的形状图相同.
故答案为:正面;
(2)如图所示:
(3)如图所示:
22.(1)解:由该几何体的三视图,可得这个几何体是圆柱.
故答案为:圆柱.
(2)
解:由该几何体的三视图可知:该圆柱的高为10,底面直径为6,
∴这个几何体的体积为:.
23.解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影,如图所示:
(2)∵DF∥AC,
∴∠ACB=∠DFE,
∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF,
∴,
∵AB=3m,BC=2m,EF=6m,
∴,
∴DE=9m;
答:旗杆DE的高度为9m.
24.(1)解:DE在阳光下的投影是EF如图所示;
(2)
在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,
∵△ABC∽△DEF,AB=5m,BC=3m,EF=6m,
∴,
∴,
∴DE=10(m),
答:DE的长为10m.
25.(1)如图,点为路灯的位置;
(2)作垂直地面,如图,0步,步,,
∵,
∴,
∴,即,解得,
∵,
∴,
∴,即,
解得.
答:路灯的高,影长为步.
26.解:延长OD,
∵DO⊥BF,
∴∠DOE=90°,
∵OD=1m,OE=1m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=x m,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴,
,
解得:x=4.
经检验:x=4是原方程的解.
答:围墙AB的高度是4m.
27.(1)解:由题意得,
∵,
∴∽,
则
解得:,
,
故两路灯之间的距离为米;
(2)
解:两影长之和为定值,定值为米.
理由:如图,设米.
∵,
∴△CPK∽△EAK,△CPQ∽△HBQ,
∴,,
则,,
∵
∴,
,
解得,
两影长之和为定值,定值为米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
