4.4 角的比较 综合练习题（含答案）

中小学教育资源及组卷应用平台
北师大版七年级数学上册第四章《4.角的比较》综合练习题（含答案）
一、单选题
1．若，，，则（ ）
A． B． C． D．
2．把10°36″用度表示为（　　）
A．10.6° B．10.001° C．10.01° D．10.1°
3．已知与都小于平角，在平面内把这两个角的一条边重合，若的另一条边恰好落在的内部，则（）．
A． B． C． D．不能比较与的大小
4．下列度分秒运算中，正确的是（　　）
A．48°39′+67°31′＝115°10′ B．90°﹣70°39′＝20°21′
C．21°17′×5＝185°5′ D．180°÷7＝25°43′（精确到分）
5．计算：的值为（ ）
A． B． C． D．
6．如图，把一张长方形的纸片沿着EF折叠，点C、D分别落在M、N的位置，且∠MFB＝∠MFE．则∠EFM的度数为（　　）
A．30° B．36° C．45° D．72°
7．如图，直线与相交于点，一直角三角尺的直角顶点与点重合，平分，现将三角尺以每秒的速度绕点顺时针旋转，同时直线也以每秒的速度绕点顺时针旋转，设运动时间为秒（），当平分时，的值为（　 ）
A． B． C．或 D．或
8．已知∠AOB=30°，∠BOC=45°，则∠AOC等于（ ）
A．15° B．75° C．15°或75° D．不能确定
二、填空题
9．=____度____分____秒；=______度．
10．单位换算：56°10′48″＝_____°．
11．12.3°=________°______′；=_________°．
12．如图，将一块三角板的直角顶点放在直尺的一边上，当时， _________．
13．如图，已知点O在直线AB上，OC⊥OD，∠BOD：∠AOC＝3：2，那么∠BOD＝___度．
14．把一副三角尺按如图所示拼在一起，如图，其中B，C，D三点在同一条直线上，∠ACB=45°，∠DCE=60°．
（1）若CM和CN分别平分∠ACB和∠DCE，如图1，则∠MCN的度数为___________；
（2）若CM平分∠BCE，CN平分∠DCA，如图2，则∠MCN的度数为___________．
三、解答题
15．将一副三角尺叠放在一起：
（1）如图①，若∠1＝4∠2，请计算出∠CAE的度数；
（2）如图②，若∠ACE＝2∠BCD，请求出∠ACD的度数．
16．如图，已知∠BOC＝2∠AOC，OD平分∠AOB，且∠COD＝20°，求∠AOB的度数．
17．如图，将一副三角板放到一起可以擦除怎样的数学火花呢？福山区某学校两个数学兴趣小组对一副三角板进行了以下两种方式的摆放组合．已知一副三角板重合的顶点记为点O，作射线OE平分∠AOC，射线OF平分∠BOD，来研究一下45°三角板不动，30°三角板绕重合的顶点O旋转时，∠EOF的度数如何变化．
【A组研究】
在同一平面内，将这副三角板的的两个锐角顶点重合（图中点O），此时∠AOB=45°，∠COD=30°将三角板OCD绕点O转动．
（1）如图①，当射线OB与OC重合时，则∠EOF的度数为___________；
（2）如图②，将∠COD绕着点O顺时针旋转，设，∠EOF的度数是否发生变化？如果不变，请根据图②求出∠EOF的度数；如果变化，请简单说明理由．
【B组研究】
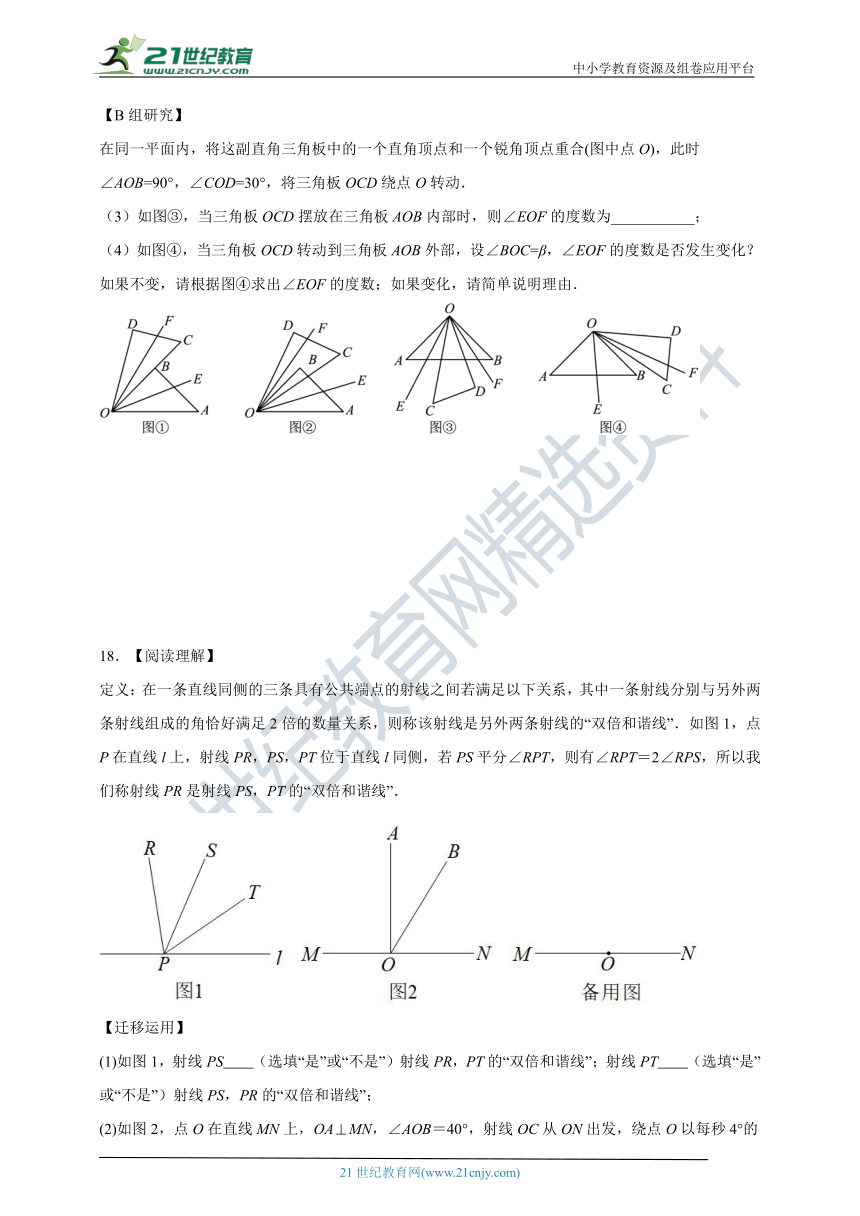
在同一平面内，将这副直角三角板中的一个直角顶点和一个锐角顶点重合(图中点O)，此时∠AOB=90°，∠COD=30°，将三角板OCD绕点O转动．
（3）如图③，当三角板OCD摆放在三角板AOB内部时，则∠EOF的度数为___________；
（4）如图④，当三角板OCD转动到三角板AOB外部，设∠BOC=β，∠EOF的度数是否发生变化？如果不变，请根据图④求出∠EOF的度数；如果变化，请简单说明理由．
18．【阅读理解】
定义：在一条直线同侧的三条具有公共端点的射线之间若满足以下关系，其中一条射线分别与另外两条射线组成的角恰好满足2倍的数量关系，则称该射线是另外两条射线的“双倍和谐线”．如图1，点P在直线l上，射线PR，PS，PT位于直线l同侧，若PS平分∠RPT，则有∠RPT＝2∠RPS，所以我们称射线PR是射线PS，PT的“双倍和谐线”．
【迁移运用】
(1)如图1，射线PS　　（选填“是”或“不是”）射线PR，PT的“双倍和谐线”；射线PT　　（选填“是”或“不是”）射线PS，PR的“双倍和谐线”；
(2)如图2，点O在直线MN上，OAMN，∠AOB＝40°，射线OC从ON出发，绕点O以每秒4°的速度逆时针旋转，运动时间为t秒，当射线OC与射线OA重合时，运动停止．
①当射线OA是射线OB，OC的“双倍和谐线”时，求t的值；
②若在射线OC旋转的同时，∠AOB绕点O以每秒2°的速度逆时针旋转，且在旋转过程中，射线OD平分∠AOB．当射线OC位于射线OD左侧且射线OC是射线OM，OD的“双倍和谐线”时，求∠CON的度数．
19．已知∠AOB和∠COD均为锐角，∠AOB＞∠COD，OP平分∠AOC，OQ平分∠BOD，将∠COD绕着点O逆时针旋转，使∠BOC=α（0≤α＜180°）
（1）若∠AOB=60°，∠COD=40°，
①当α=0°时，如图1，则∠POQ=　 　；
②当α=80°时，如图2，求∠POQ的度数；
③当α=130°时，如图3，请先补全图形，然后求出∠POQ的度数；
（2）若∠AOB=m°，∠COD=n°，m＞n，则∠POQ=　 　，（请用含m、n的代数式表示）．
20．已知，OC、OD是过点O的射线，射线OM、ON分别平分∠AOC和∠DOB．
(1)如图①，若OC、OD是∠AOB的三等分线，则______°
(2)如图②，若，，则______°
(3)如图③，在∠AOB内，若，则______°
(4)将（3）中的∠COD绕着点O逆时针旋转到∠AOB的外部（，），求此时∠MON的度数。
参考答案
1．A2．C3．A4．D5．B6．D7．D8．C
9． 55 39 36 43.54
10．56.18
11． 12 18 15.5
12．53°
13．54
14． 52.5°
15．解：（1）∵∠BAC＝90°，
∴∠1+∠2＝90°，
∵∠1＝4∠2，
∴4∠2+∠2＝90°，
∴∠2＝18°，
又∵∠DAE＝90°，
∴∠1+∠CAE＝∠2+∠1＝90°，
∴∠CAE＝∠2＝18°；
（2）∵∠ACE+∠BCE＝90°，∠BCD+∠BCE＝60°，
∴∠ACE﹣∠BCD＝30°，
又∠ACE＝2∠BCD，
∴2∠BCD﹣∠BCD＝30°，∠BCD＝30°，
∴∠ACD＝∠ACB+∠BCD＝90°+30°＝120°．
16．解：设∠AOC＝x，则∠BOC＝2x．
∴∠AOB＝3x．
又OD平分∠AOB，
∴∠AOD＝1.5x．
∴∠COD＝∠AOD﹣∠AOC＝1.5x﹣x＝20°．
∴x＝40°
∴∠AOB＝120°．
17．解: (1) ，OE平分∠AOC，OF平分∠BOD，
，
故答案为：；
(2)不变；
∵，
∴，
∵OE平分∠AOC，OF平分∠BOD，
∴，
∴，
，
=，
=，
=；
(3) ，
，
，
，
，
，
，
故答案为：60°；
(4)不变，
由题意得，，
，
=，
=，
=．
18．（1）解：∵PS平分∠RPT，
∴∠RPS=∠TPS，
∴射线PS不是射线PR，PT的“双倍和谐线”；
∵PS平分∠RPT，
∴∠TPR=2∠TPS．
∴射线PT是射线PS，PR的“双倍和谐线”．
故答案为：不是；是；
（2）①由题意得：∠AOC=90°-4°t，∠AOB=40°．
∵射线OA是射线OB，OC的“双倍和谐线”，
∴∠AOC=2∠AOB或∠AOB=2∠AOC．
当∠AOC=2∠AOB时，如图，
则：90-4t=2×40．
解得：t=，
当∠AOB=2∠AOC时，如图，
则：40=2（90-4t）．
解得：t=，
综上，当射线OA是射线OB，OC的“双倍和谐线”时，t的值为或；
②由题意得：∠CON=4°t，∠AON=90°+2°t，∠AOD=20°，∠DON=∠AON-∠AOD=70°+2°t．
∵当射线OC与射线OA重合时，运动停止，
∴此时∠AON=∠CON．
∴90+2t=4t．
∴t=45．
∴当t=45秒时，运动停止，此时∠AON=180°．
∵射线OC位于射线OD左侧且射线OC是射线OM，OD的“双倍和谐线”，
∴∠COM=2∠COD或∠COD=2∠COM．
当∠COM=2∠COD时，如图，
即：180°-∠CON=2（∠CON-∠DON），
则：180-4t=2（4t-70-2t）．
解得：t=40．
∴∠CON=4°×40=160°．
当∠COD=2∠COM时，如图，
即：∠CON-∠DON=2（180°-∠CON）．
则：4t-（70+2t）=2（180-4t）．
解得：t=43．
∴∠CON=4°×43=172°．
综上，当射线OC位于射线OD左侧且射线OC是射线OM，OD的“双倍和谐线”时，∠CON的度数为160°或172°．
19．解：（1）①∵∠AOB=60°，∠COD=40°，OP平分∠AOC，OQ平分∠BOD，
∴∠BOP=∠AOB=30°，∠BOQ=∠COD=20°，
∴∠POQ=50°，
故答案为：50°；
②解：∵∠AOB=60°，∠BOC=α=80°，
∴∠AOC=140°，
∵OP平分∠AOC，
∴∠POC=∠AOC=70°，
∵∠COD=40°，∠BOC=α=80°，
且OQ平分∠BOD，
同理可求∠DOQ=60°，
∴∠COQ=∠DOQ-∠DOC=20°，
∴∠POQ=∠POC-∠COQ=70°-20°=50°；
③解：补全图形如图3所示，
∵∠AOB=60°，∠BOC=α=130°，
∴∠AOC=360°-60°-130°=170°，
∵OP平分∠AOC，
∴∠POC=∠AOC=85°，
∵∠COD=40°，∠BOC=α=130°，
且OQ平分∠BOD，
同理可求∠DOQ=85°，
∴∠COQ=∠DOQ-∠DOC=85°-40°=45°，
∴∠POQ=∠POC+∠COQ=85°+45°=130°；
（2）当∠AOB=m°，∠COD=n°时，如图2，
∴∠AOC= m°+ °，
∵OP平分∠AOC，
∴∠POC=(m°+ °)，
同理可求∠DOQ=(n°+ °)，
∴∠COQ=∠DOQ-∠DOC=(n°+ °)- n°=(-n°+ °)，
∴∠POQ=∠POC-∠COQ=(m°+ °)-(-n°+ °)
=m°+n°，
当∠AOB=m°，∠COD=n°时，如图3，
∵∠AOB=m°，∠BOC=α，
∴∠AOC=360°-m°-°，
∵OP平分∠AOC，
∴∠POC=∠AOC=180°(m°+ °)，
∵∠COD=n°，∠BOC=α，
且OQ平分∠BOD，
同理可求∠DOQ=(n°+ °)，
∴∠COQ=∠DOQ-∠DOC=(n°+ °)-n°=(-n°+ °)，
∴∠POQ=∠POC+∠COQ=180°(m°+ °)+(-n°+ °)
=180°-m°-n°，
综上所述，若∠AOB=m°，∠COD=n°，则∠POQ=m°+n°或180°-m°-n°．
故答案为：m°+n°或180°-m°-n°．
20．（1）解：、是的三等分线，
，
射线、分别平分和，
，，
；
故答案为80；
（2）解：射线、分别平分和，
，，
，
，，
，
；
故答案为80；
（3）解：射线、分别平分和，
，，
，
，，
，
，
；
故答案为；
（4）解：反向延长、得到、，如图，
当、在内部，
设，则，
，，
；
当、在内部，可计算得到；
当、在内部，可计算得到；
当、在内部，可计算得到．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)