4.4 一次函数的应用 课时练习题(含答案)
文档属性
| 名称 | 4.4 一次函数的应用 课时练习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1013.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 22:07:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版八年级数学上册第四章《4.一次函数的应用》
课时练习题(含答案)
一、单选题
1.“漏壶”是一种古代计时器,如图所示,在壶内盛一定量的水,水从壶底的小孔漏出,壶内壁画有刻度,人们根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度,不考虑水量变化对压力的影响,下列图象能表示y与x对应关系的是( )
A. B. C. D.
2.某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:)与工作时间t(单位:h)之间的函数关系如图所示.则该绿化组提高工作效率前每小时完成的绿化面积是( )
A. B. C. D.
3.为了让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m2,打开进水口注水时,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图像如图所示,下列说法错误的是( )
A.注水2小时,游泳池的蓄水量为380m3 B.该游泳池内开始注水时已经蓄水100m3
C.注水2小时,还需注水100m3,可将游泳池注满 D.每小时可注水190m3
4.现有甲、乙两个长方体蓄水池,将甲池中的水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)(小时)之间的函数图象如图所示,当甲、乙两池中水的深度相同时,y的值为( )
A.3.2米 B.4米 C.4.2米 D.4.8米
5.在平面直角坐标系中,长方形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点,若E为x轴上的一个动点,当△CDE的周长最小时,求点E的坐标( )
A.(一3,0) B.(3,0) C.(0,0) D.(1,0)
6.如图,在矩形中,,,动点沿折线从点开始运动到点.设运动的路程为,的面积为,那么与之间的函数关系的图象大致是( )
A. B.
C. D.
7.已知A、B两地相距600米,甲、乙两人同时从A地出发前往B地,所走路程y(米)与行驶时间x(分)之间的函数关系如图所示,则下列说法中:①甲每分钟走100米;②2分钟后,乙每分钟走50米;③甲比乙提前3分钟到达B地;④当x=2或6时,甲乙两人相距100米.其中,正确的是( )
A.①②③ B.②③④ C.①②④ D.①②
8.、两地相距,甲骑摩托车从地匀速驶向地.当甲行驶小时途径地时,一辆货车刚好从地出发匀速驶向地,当货车到达地后立即掉头以原速匀速驶向地.如图表示两车与地的距离和甲出发的时间的函数关系.则下列说法错误的是( )
A.甲行驶的速度为 B.货车返回途中与甲相遇后又经过甲到地
C.甲行驶小时时货车到达地 D.甲行驶到地需要
二、填空题
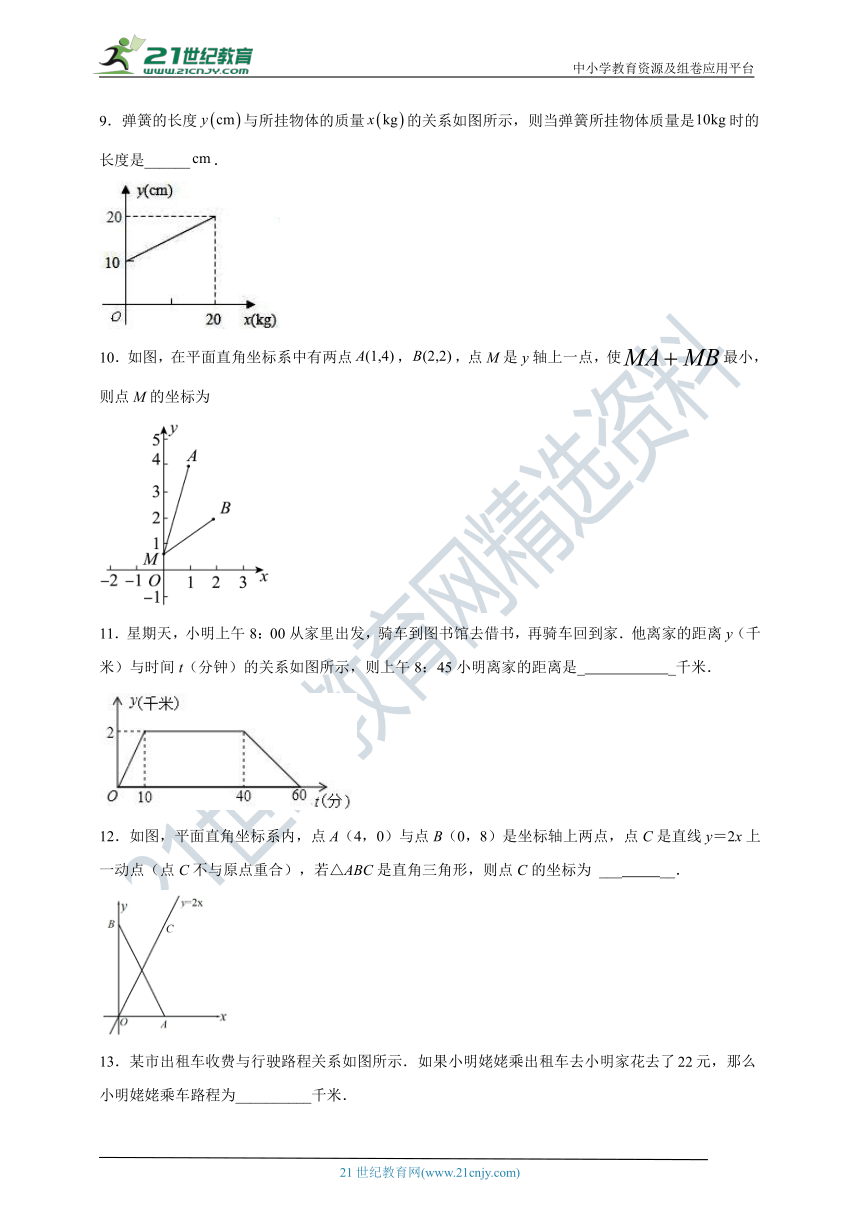
9.弹簧的长度与所挂物体的质量的关系如图所示,则当弹簧所挂物体质量是时的长度是______.
10.如图,在平面直角坐标系中有两点,,点M是y轴上一点,使最小,则点M的坐标为
11.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是_ _千米.
12.如图,平面直角坐标系内,点A(4,0)与点B(0,8)是坐标轴上两点,点C是直线y=2x上一动点(点C不与原点重合),若△ABC是直角三角形,则点C的坐标为 ___ __.
13.某市出租车收费与行驶路程关系如图所示.如果小明姥姥乘出租车去小明家花去了元,那么小明姥姥乘车路程为__________千米.
14.甲、乙两车从A地出发,匀速驶往B地.乙车出发1h后,甲车才沿相同的路线开始行驶.甲车先到达B地并停留30分钟后,又以原速按原路线返回,直至与乙相遇.图中的折线段表示从开始到相遇止,两车之间的距离y(km)与甲车行驶的时间x(h)的函数关系的图象,则
(1)___________________.
(2)___________________.
三、解答题
15.如图一次函数的图象经过点,与x轴交于点B,与正比例函数的图象交于点C,点C的横坐标为1.
(1)求的函数表达式.
(2)若点D在y轴负半轴,且满足,求点D的坐标.
(3)若,请直接写出x的取值范围.
16.某公交车每月的支出费用为4000元,每月的乘车人数(人)与每月的利润(元)的变化关系如下表所示:(利润=收入费用-支出费用,每位乘客的公交票价是固定不变的):
(人) 500 1000 1500 2000 2500 3000 …
(元) 0 1000 2000 …
(1)在这个变化过程中,直接写出自变量和因变量;
(2)观察表中数据可知,每月乘客量达到_____人以上时,该公交车才会盈利;
(3)请你估计每月乘车人数为3500人时,每月的利润为______元;
(4)根据表格直接写出与的表达式,并求出5月份乘客量需达多少人时,可获得5000元的利润.
17.某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 10 15 20 … x
方式一的总费用(元) 150 175 ______ … ______
方式二的总费用(元) 90 135 ______ … ______
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
18.如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过A(-6,0),B(0,3)两点,点C在直线AB上,C的纵坐标为4.
(1)求k、b的值及点C坐标;
(2)若点D为直线AB上一动点,且△OBC与△OAD的面积相等,试求点D的坐标.
19.一列快车和一列慢车同时从甲地出发,分别以速度、(单位:,且)匀速驶向乙地.快车到达乙地后停留了,沿原路仍以速度匀速返回甲地,设慢车行驶的时间为,两车之间的距离为,图中的折线表示从慢车出发至慢车到达乙地的过程中,与之间的函数关系.
(1)甲乙两地相距______;点实际意义:______;
(2)求,的值;
(3)慢车出发多长时间后,两车相距?
20.如图①,在A、B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地,两车同时出发,匀速行驶,图②是客车、货车离 C站的路程、(km)与行驶时间x(h)之间的函数图像.
(1)客车的速度是 km/h;
(2)求货车由 B地行驶至 A地所用的时间;
(3)求点E的坐标,并解释点 E的实际意义。
参考答案
1.B2.D3.D4.A5.D6.D7.C8.C
9.15
10.##
11.1.5##32
12.(4,8)或(,)或(,)
13.13
14. 50 ##4.3125
15.解:(1)∵一次函数与正比例函数的图象交于点C,点C的横坐标为1,
∴把x=1代入正比例函数得:,
∴点,
∴把点、代入一次函数得:
,解得:,
∴AB的函数解析式为;
(2)由(1)得:,AB的函数解析式为,
∴令y=0时,则有,
∴点,
∴OB=4,
令表示点C的横坐标,表示点C的纵坐标,则由图象可得:,
∵,
∴,
∴,
∴,
∵点D在y轴负半轴,
∴;
(3)由图象可得:
当时,则x的取值范围为.
16.解:(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
故答案为每月的乘车人数x,每月的利润y;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
故答案为2000;
(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元;
故答案为3000;
(4)设与的表达式为y=kx+b,则依题意得:
解得:
∴与的表达式为;
当时,
.
解得.
答:5月乘车人数为4500人时,可获得利润5000元.
17.(Ⅰ)200,,180,.
(Ⅱ)方式一:,解得.
方式二:,解得.
∵,
∴小明选择方式一游泳次数比较多.
(Ⅲ)设方式一与方式二的总费用的差为元.
则,即.
当时,即,得.
∴当时,小明选择这两种方式一样合算.
∵,
∴随的增大而减小.
∴当时,有,小明选择方式二更合算;
当时,有,小明选择方式一更合算.
18.(1)解:(1)依题意得:
解得
∴
∵点C在直线AB上,C的纵坐标为4
点C坐标为(2,4)
(2)∵B(0,3),C的纵坐标为4
∴
∴
设点D点坐标为,又点A(-6,0)
∴
解得
当时
当时
∴点D坐标为(-4,1)或(-8,-1)
19.(1)由图象知,甲、乙两地之间的距离为900km;点实际意义:快车到达乙地;
(2)根据图象,得慢车的速度为=60(km/h),
快车的速度为:900÷=150(km/h),
∴a==8,
b==14;
(3)
由题意得A(=6,540),B(8,540-60×2=420),C(=10,0),D(14,14×60=840),分别代入y=kx+b,
可得线段OA所表示的y与x之间的函数表达式为y3=90x(0≤x<6);
线段AB所表示的y与x之间的函数表达式为y1=-60x+900(6≤x<8)
线段CD所表示的y与x之间的函数表达式为y2=210x-2100(10≤x<14),
①线段OA所表示的y与x之间的函数表达式为y3=90x(0≤x<6),
令y3=480,得x=,
②线段AB所表示的y与x之间的函数表达式为y1=-60x+900(6≤x<8),
令y1=480,得x=7,
③线段CD所表示的y与x之间的函数表达式为y2=210x-2100(10≤x<14),
令y2=480,得x=.
答:慢车出发h、7h、h后,两车相距480km.
20.解:(1)由图象可得,客车的速度是:360÷6=60(km/h),
故答案为:60;
(2)由图象可得,
货车由B地到A地的所用的时间是:(60+360)÷(60÷2)=14(h),
即货车由B地到A地的所用的时间是14h;
(3)设客车由A到C对应的函数解析式为y=kx+b,
则,得,
即客车由A到C对应的函数解析式为y=-60x+360;
根据(2)知点P的坐标为(14,360),设货车由C到A对应的函数解析式为y=mx+n,
则,得,
即货车由C到A对应的函数解析式为y=30x-60;
∴,得,
∴点E的坐标为(,80),
故点E代表的实际意义是在行驶h时,客车和货车相遇,相遇时两车离C站的距离为80km.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版八年级数学上册第四章《4.一次函数的应用》
课时练习题(含答案)
一、单选题
1.“漏壶”是一种古代计时器,如图所示,在壶内盛一定量的水,水从壶底的小孔漏出,壶内壁画有刻度,人们根据壶中水面的位置计算时间.用x表示漏水时间,y表示壶底到水面的高度,不考虑水量变化对压力的影响,下列图象能表示y与x对应关系的是( )
A. B. C. D.
2.某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:)与工作时间t(单位:h)之间的函数关系如图所示.则该绿化组提高工作效率前每小时完成的绿化面积是( )
A. B. C. D.
3.为了让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m2,打开进水口注水时,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图像如图所示,下列说法错误的是( )
A.注水2小时,游泳池的蓄水量为380m3 B.该游泳池内开始注水时已经蓄水100m3
C.注水2小时,还需注水100m3,可将游泳池注满 D.每小时可注水190m3
4.现有甲、乙两个长方体蓄水池,将甲池中的水匀速注入乙池,甲、乙两个蓄水池中水的深度y(米)(小时)之间的函数图象如图所示,当甲、乙两池中水的深度相同时,y的值为( )
A.3.2米 B.4米 C.4.2米 D.4.8米
5.在平面直角坐标系中,长方形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点,若E为x轴上的一个动点,当△CDE的周长最小时,求点E的坐标( )
A.(一3,0) B.(3,0) C.(0,0) D.(1,0)
6.如图,在矩形中,,,动点沿折线从点开始运动到点.设运动的路程为,的面积为,那么与之间的函数关系的图象大致是( )
A. B.
C. D.
7.已知A、B两地相距600米,甲、乙两人同时从A地出发前往B地,所走路程y(米)与行驶时间x(分)之间的函数关系如图所示,则下列说法中:①甲每分钟走100米;②2分钟后,乙每分钟走50米;③甲比乙提前3分钟到达B地;④当x=2或6时,甲乙两人相距100米.其中,正确的是( )
A.①②③ B.②③④ C.①②④ D.①②
8.、两地相距,甲骑摩托车从地匀速驶向地.当甲行驶小时途径地时,一辆货车刚好从地出发匀速驶向地,当货车到达地后立即掉头以原速匀速驶向地.如图表示两车与地的距离和甲出发的时间的函数关系.则下列说法错误的是( )
A.甲行驶的速度为 B.货车返回途中与甲相遇后又经过甲到地
C.甲行驶小时时货车到达地 D.甲行驶到地需要
二、填空题
9.弹簧的长度与所挂物体的质量的关系如图所示,则当弹簧所挂物体质量是时的长度是______.
10.如图,在平面直角坐标系中有两点,,点M是y轴上一点,使最小,则点M的坐标为
11.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是_ _千米.
12.如图,平面直角坐标系内,点A(4,0)与点B(0,8)是坐标轴上两点,点C是直线y=2x上一动点(点C不与原点重合),若△ABC是直角三角形,则点C的坐标为 ___ __.
13.某市出租车收费与行驶路程关系如图所示.如果小明姥姥乘出租车去小明家花去了元,那么小明姥姥乘车路程为__________千米.
14.甲、乙两车从A地出发,匀速驶往B地.乙车出发1h后,甲车才沿相同的路线开始行驶.甲车先到达B地并停留30分钟后,又以原速按原路线返回,直至与乙相遇.图中的折线段表示从开始到相遇止,两车之间的距离y(km)与甲车行驶的时间x(h)的函数关系的图象,则
(1)___________________.
(2)___________________.
三、解答题
15.如图一次函数的图象经过点,与x轴交于点B,与正比例函数的图象交于点C,点C的横坐标为1.
(1)求的函数表达式.
(2)若点D在y轴负半轴,且满足,求点D的坐标.
(3)若,请直接写出x的取值范围.
16.某公交车每月的支出费用为4000元,每月的乘车人数(人)与每月的利润(元)的变化关系如下表所示:(利润=收入费用-支出费用,每位乘客的公交票价是固定不变的):
(人) 500 1000 1500 2000 2500 3000 …
(元) 0 1000 2000 …
(1)在这个变化过程中,直接写出自变量和因变量;
(2)观察表中数据可知,每月乘客量达到_____人以上时,该公交车才会盈利;
(3)请你估计每月乘车人数为3500人时,每月的利润为______元;
(4)根据表格直接写出与的表达式,并求出5月份乘客量需达多少人时,可获得5000元的利润.
17.某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 10 15 20 … x
方式一的总费用(元) 150 175 ______ … ______
方式二的总费用(元) 90 135 ______ … ______
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
18.如图,在平面直角坐标系中,点O为坐标原点,直线y=kx+b经过A(-6,0),B(0,3)两点,点C在直线AB上,C的纵坐标为4.
(1)求k、b的值及点C坐标;
(2)若点D为直线AB上一动点,且△OBC与△OAD的面积相等,试求点D的坐标.
19.一列快车和一列慢车同时从甲地出发,分别以速度、(单位:,且)匀速驶向乙地.快车到达乙地后停留了,沿原路仍以速度匀速返回甲地,设慢车行驶的时间为,两车之间的距离为,图中的折线表示从慢车出发至慢车到达乙地的过程中,与之间的函数关系.
(1)甲乙两地相距______;点实际意义:______;
(2)求,的值;
(3)慢车出发多长时间后,两车相距?
20.如图①,在A、B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地,两车同时出发,匀速行驶,图②是客车、货车离 C站的路程、(km)与行驶时间x(h)之间的函数图像.
(1)客车的速度是 km/h;
(2)求货车由 B地行驶至 A地所用的时间;
(3)求点E的坐标,并解释点 E的实际意义。
参考答案
1.B2.D3.D4.A5.D6.D7.C8.C
9.15
10.##
11.1.5##32
12.(4,8)或(,)或(,)
13.13
14. 50 ##4.3125
15.解:(1)∵一次函数与正比例函数的图象交于点C,点C的横坐标为1,
∴把x=1代入正比例函数得:,
∴点,
∴把点、代入一次函数得:
,解得:,
∴AB的函数解析式为;
(2)由(1)得:,AB的函数解析式为,
∴令y=0时,则有,
∴点,
∴OB=4,
令表示点C的横坐标,表示点C的纵坐标,则由图象可得:,
∵,
∴,
∴,
∴,
∵点D在y轴负半轴,
∴;
(3)由图象可得:
当时,则x的取值范围为.
16.解:(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
故答案为每月的乘车人数x,每月的利润y;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
故答案为2000;
(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元;
故答案为3000;
(4)设与的表达式为y=kx+b,则依题意得:
解得:
∴与的表达式为;
当时,
.
解得.
答:5月乘车人数为4500人时,可获得利润5000元.
17.(Ⅰ)200,,180,.
(Ⅱ)方式一:,解得.
方式二:,解得.
∵,
∴小明选择方式一游泳次数比较多.
(Ⅲ)设方式一与方式二的总费用的差为元.
则,即.
当时,即,得.
∴当时,小明选择这两种方式一样合算.
∵,
∴随的增大而减小.
∴当时,有,小明选择方式二更合算;
当时,有,小明选择方式一更合算.
18.(1)解:(1)依题意得:
解得
∴
∵点C在直线AB上,C的纵坐标为4
点C坐标为(2,4)
(2)∵B(0,3),C的纵坐标为4
∴
∴
设点D点坐标为,又点A(-6,0)
∴
解得
当时
当时
∴点D坐标为(-4,1)或(-8,-1)
19.(1)由图象知,甲、乙两地之间的距离为900km;点实际意义:快车到达乙地;
(2)根据图象,得慢车的速度为=60(km/h),
快车的速度为:900÷=150(km/h),
∴a==8,
b==14;
(3)
由题意得A(=6,540),B(8,540-60×2=420),C(=10,0),D(14,14×60=840),分别代入y=kx+b,
可得线段OA所表示的y与x之间的函数表达式为y3=90x(0≤x<6);
线段AB所表示的y与x之间的函数表达式为y1=-60x+900(6≤x<8)
线段CD所表示的y与x之间的函数表达式为y2=210x-2100(10≤x<14),
①线段OA所表示的y与x之间的函数表达式为y3=90x(0≤x<6),
令y3=480,得x=,
②线段AB所表示的y与x之间的函数表达式为y1=-60x+900(6≤x<8),
令y1=480,得x=7,
③线段CD所表示的y与x之间的函数表达式为y2=210x-2100(10≤x<14),
令y2=480,得x=.
答:慢车出发h、7h、h后,两车相距480km.
20.解:(1)由图象可得,客车的速度是:360÷6=60(km/h),
故答案为:60;
(2)由图象可得,
货车由B地到A地的所用的时间是:(60+360)÷(60÷2)=14(h),
即货车由B地到A地的所用的时间是14h;
(3)设客车由A到C对应的函数解析式为y=kx+b,
则,得,
即客车由A到C对应的函数解析式为y=-60x+360;
根据(2)知点P的坐标为(14,360),设货车由C到A对应的函数解析式为y=mx+n,
则,得,
即货车由C到A对应的函数解析式为y=30x-60;
∴,得,
∴点E的坐标为(,80),
故点E代表的实际意义是在行驶h时,客车和货车相遇,相遇时两车离C站的距离为80km.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
