人教版必修二 第五章 抛体运动 章测试(含答案)
文档属性
| 名称 | 人教版必修二 第五章 抛体运动 章测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 722.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-11-20 08:49:13 | ||
图片预览


文档简介
人教版必修二第五章章测试(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
生活中曲线运动随处可见,关于物体做曲线运动,下列说法正确的是( )
A. 速度方向有时与曲线相切,有时与曲线的切线垂直
B. 平抛运动是匀变速曲线运动,斜抛运动是变加速曲线运动
C. 物体所受合力方向一定指向曲线的凹侧
D. 物体所受合力可能不变,但它的加速度一定改变
若已知物体运动的初速度的方向及它受到的恒定的合力的方向,如图所示,则物体运动的轨迹可能是 ( )
A. B. C. D.
一个做平抛运动的物体,初速度为,经过一段时间,它的末速度与竖直方向的夹角为,重力加速度取,则它下落的时间约为 ( )
A. B. C. D.
利用手机可以玩一种叫“扔纸团”的小游戏。如图所示,游戏时,游戏者滑动屏幕将纸团从点以速度水抛向固定在水平地面上的圆柱形废纸篓,纸团恰好从纸篓的上边沿入篓并直接打在纸篓的底角。若要让纸团进入纸篓中并直接击中篓底正中间,下列做法可行的是( )
A. 在点将纸团以小于的速度水平抛出
B. 在点将纸团以大于的速度水平抛出
C. 在点正上方某位置将纸团以小于的速度水平抛出
D. 在点正下方某位置将纸团以大于的速度水平抛出
如图所示,、两物体以相同的水平速度从坐标系原点沿轴正方向被抛出,在竖直平面内运动,落地点为;紧贴光滑的斜面运动,落地点为,和对应的坐标分别为和,不计空气阻力,下列说法正确的是( )
A. 落在点时恰好落在点 B. 先到达点
C. D.
如图所示,是长方形对角线的交点,是底边的中点,、、处的三个小球分别沿图示方向做平抛运动,下列表述不正确的是( )
A. 若、、处三球同时抛出,三球不可能在落地前相遇
B. 要、处两球在空中相遇,则球必须先抛出
C. 若、处两球能在地面相遇,则、在空中运动的时间之比为:
D. 若、处两球在点相遇,则一定满足
如图所示,小船以大小为、方向与上游河岸成的速度在静水中的速度从处过河,经过时间正好到达正对岸的处。现要使小船在更短的时间内过河并且也正好到达正对岸处,在水流速度不变的情况下,可采取下列方法中的哪一种( )
A. 只要增大大小,不必改变角 B. 只要增大角,不必改变大小
C. 在增大的同时,也必须适当增大角 D. 在增大的同时,也必须适当减小角
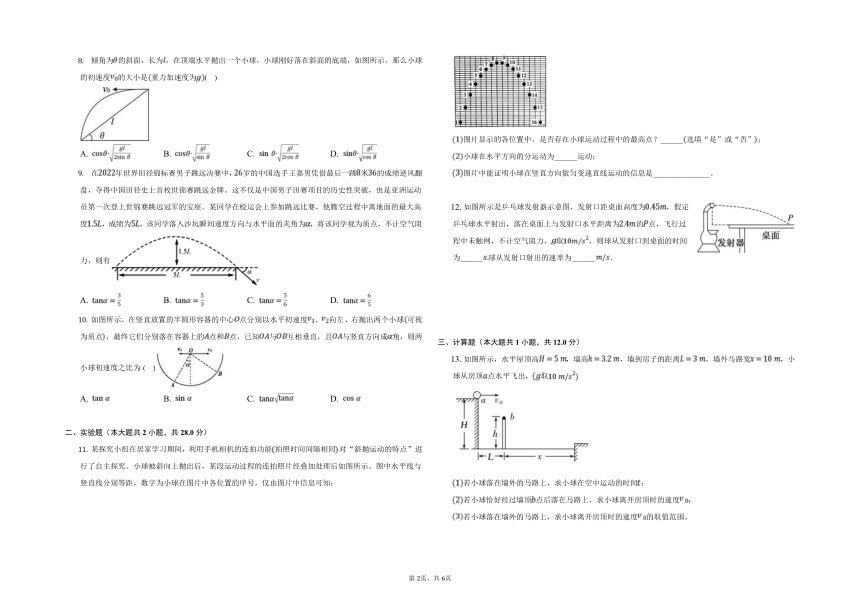
倾角为的斜面,长为,在顶端水平抛出一个小球,小球刚好落在斜面的底端,如图所示,那么小球的初速度的大小是重力加速度为( )
A. B. C. D.
在年世界田径锦标赛男子跳远决赛中,岁的中国选手王嘉男凭借最后一跳米的成绩逆风翻盘,夺得中国田径史上首枚世锦赛跳远金牌。这不仅是中国男子田赛项目的历史性突破,也是亚洲运动员第一次登上世锦赛跳远冠军的宝座。某同学在校运会上参加跳远比赛,他腾空过程中离地面的最大高度,成绩为,该同学落入沙坑瞬间速度方向与水平面的夹角为,将该同学视为质点,不计空气阻力,则有
A. B. C. D.
如图所示,在竖直放置的半圆形容器的中心点分别以水平初速度、向左、右抛出两个小球可视为质点,最终它们分别落在容器上的点和点,已知与互相垂直,且与竖直方向成角,则两小球初速度之比为( )
A. B. C. D.
二、实验题(本大题共2小题,共28.0分)
某探究小组在居家学习期间,利用手机相机的连拍功能拍照时间间隔相同对“斜抛运动的特点”进行了自主探究。小球被斜向上抛出后,某段运动过程的连拍照片经叠加处理后如图所示。图中水平线与竖直线分别等距,数字为小球在图片中各位置的序号,仅由图片中信息可知:
图片显示的各位置中,是否存在小球运动过程中的最高点?______选填“是”或“否”;
小球在水平方向的分运动为______运动;
图片中能证明小球在竖直方向做匀变速直线运动的信息是_______________。
如图所示是乒乓球发射器示意图,发射口距桌面高度为,假定乒乓球水平射出,落在桌面上与发射口水平距离为的点,飞行过程中未触网,不计空气阻力,取,则球从发射口到桌面的时间为______球从发射口射出的速率为______ .
三、计算题(本大题共1小题,共12.0分)
如图所示,水平屋顶高,墙高,墙到房子的距离,墙外马路宽,小球从房顶点水平飞出,取
若小球落在墙外的马路上,求小球在空中运动的时间;
若小球恰好经过墙顶点后落在马路上,求小球离开房顶时的速度;
若小球落在墙外的马路上,求小球离开房顶时的速度的取值范围。
答案和解析
1.【答案】
【解析】
【分析】
本题考查了物体做曲线运动;解决本题的关键知道合运动是直线运动还是曲线运动取决于合速度方向与合加速度方向是否在同一条直线上,以及会根据平行四边形定则判断合速度与分速度的大小关系。
曲线运动的条件,合外力与速度不在一条直线上,速度方向时刻变化,故曲线运动一定是变速运动,曲线运动的速度的方向与该点曲线的切线方向相同;
平抛运动、斜抛运动的加速度不变,均做匀变速曲线运动,速度均匀变化;
物体做曲线运动的加速度的方向指向曲线的凹侧;
在恒力作用下,物体可以做曲线运动。
【解答】
A.在曲线运动中,质点的速度方向一定沿着轨迹的切线方向,故A错误;
B.平抛运动是匀变速曲线运动,斜抛运动也是匀变速曲线运动,故B错误;
C.根据曲线运动的受力特点可知,做曲线运动的物体其所受合力一定指向轨迹的凹侧,故C正确;
D.做曲线运动的物体可以受恒力作用,其加速度可以保持不变,如平抛运动,故D错误。
故选。
2.【答案】
【解析】
【分析】本题考查物体做曲线运动的条件,做曲线运动的物体,速度方向沿着曲线上该点的切线方向,合力的方向与速度方向不共线,且指向曲线的凹侧,运动轨迹在合力与速度之间。
【解答】
物体做曲线运动时,速度沿曲线的切线方向,合力方向和速度方向不共线,且指向曲线的凹侧,则运动轨迹在合力与速度之间,且向合力的方向弯曲,故B正确,ACD错误。
3.【答案】
【解析】解:
物体做平抛运动,根据题意,结合平抛运动的特点可知,解得,故ABC错误,D正确.
4.【答案】
【解析】
【分析】
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合运动学公式分析判断。
本题运用平抛运动的知识分析处理生活中的问题,比较简单,关键运用运动的分解方法得到水平位移的表达式。
【解答】
A.在点的初速度减小,则下降到框上沿这段时间内,水平位移变小,则小球不能进入筐中,故A错误。
B.在点的初速度增大,则下降到筐底的时间内,水平位移增大,不能直接击中筐底的正中间,故B错误。
C.在点正上方某位置将小球以小于的速度水平抛出,根据知,水平位移可以减小,也不会与框的左边沿相撞,落在筐底的正中间,故C正确。
D.在点正下方某位置将小球以大于的速度水平抛出,则小球能进筐,但不能击中篓底正中间。故D错误。
故选C。
5.【答案】
【解析】
【分析】
小球做平抛运动,小球做类平抛运动,根据牛顿第二定律求出在斜面上的加速度,结合下落的高度和沿斜面下落的位移,求出运动的时间,进行比较.通过初速度和运动的时间比较沿轴方向上的位移。
解决本题的关键掌握处理类平抛运动的方法,通过水平方向和沿斜面向下方向的规律进行分析求解。
【解答】
对于球,运动的时间为:,,
对于球,,根据,解得:,
可知,,.
沿轴方向上的位移为:,知故ABC错误,D正确。
6.【答案】
【解析】解:若、、处三球同时抛出,竖直分运动均是自由落体运动,故处、处的小球不可能与处小球相遇,故A正确;
B.由于平抛运动的竖直分运动是自由落体运动,要、处两球在空中相遇,则球必须先抛出,故B正确;
C.若、处两球能在地面相遇,根据可知,两个球运动时间之比为:,故C错误;
D.若、处两球在点相遇,由于水平分运动是匀速直线运动,水平分位移相等,时间也相等,故水平分速度相等,即初速度相等,则一定满足,故D正确。
本题选择不正确的,
故选:。
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度比较运动的时间,结合水平位移和时间比较初速度。
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道运动的时间由高度决定,初速度和时间共同决定水平位移。
7.【答案】
【解析】
【分析】
由题意可知,小船在更短的时间内过河并且也正好到达正对岸处,则船在水流方向的分速度不变,船在垂直河岸方向的分速度要增大,根据平行四边形定则,即可求解。
考查运动的合成与分解,掌握平行四边形定则的应用,注意要使小船在更短的时间内过河并且也正好到达正对岸处,必须满足船在水流方向的分速度不变,且垂直河岸的分速度要增大。
【解答】
A.若只增大大小,不必改变角,则船在水流方向的分速度增大,因此船不可能垂直达到对岸,故A错误;
B.若只增大角,不必改变大小,同理可知,水流方向的分速度在减小,而垂直河岸的分速度在增大,船不可能垂直到达对岸,故B错误;
C.若在增大的同时,也必须适当增大角,这样才能保证水流方向的分速度不变,而垂直河岸的分速度在增大,则船还能垂直达到对岸,且时间更短,故C正确;
D.若增大的同时,也必须适当减小角,则水流方向的分速度增大,不能垂直到达对岸,故D错误。
故选C。
8.【答案】
【解析】
【分析】解决本题的关键关键知道平抛运动在水平方向和竖直方向上的运动规律,知道平抛运动的时间由高度决定,初速度和时间共同决定水平位移。
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据下落的高度求出运动的时间,再根据水平位移和时间求出小球的初速度。
【解答】
在竖直方向上有:,解得,
则初速度,故A正确,BCD错误,故选:。
9.【答案】
【解析】
【分析】
根据平抛运动的推论进行求解即可。
本题考查抛体运动的处理规律,掌握运动的合成与分解的应用,要注意运动员在水平方向做匀速直线运动,从最高点向下竖直方向做自由落体运动。
【解答】
运动员从最高点到落地的过程做平抛运动,根据平抛运动的推论,速度的反向延长线过
水平位移的中点,则有:,故ABC错误;D正确。
故选D。
10.【答案】
【解析】
【分析】
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据平抛运动水平位移和竖直位移的关系确定两小球运动时间之比和初速度大小之比。
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住两球竖直位移和水平位移之间的关系,运用运动学公式研究。
【解答】
由几何关系可知:左小球下降的竖直高度为,右小球下降的竖直高度为
由平抛运动规律可知:;
由此可得:时间之比
由几何关系可知:两小球水平运动的位移分别为:
,
由平抛运动规律可知:,,
由此可得:两小球的初速度之比为,故ABD错误,C正确。
故选C。
11.【答案】否;匀速直线;
任意连续相等时间内的竖直位移差相等。
【解析】
【分析】
本题考查了对斜抛运动的认识。
最高点速度方向应是水平方向;
根据相连点的水平间距解答;
根据匀变速直线运动的推论和竖直方向的位移差分析。
【解答】
最高点速度方向应是水平方向,用平滑的曲线连接图中各点,如图:
各点的速度方向均不是水平,所以图片显示的各位置中不存在小球运动过程中的最高点;
相邻位置之间的水平间距相等,且拍照时间间隔相同,所以小球在水平方向的分运动为匀速直线运动;
观察图片可知:任意连续相等时间内的竖直位移差相等,所以图片中能证明小球在竖直方向做匀变速直线运动。
12.【答案】
【解析】解:乒乓球水平射出后做平抛运动,其加速度等于重力加速度,始终保持不变,由得:
;
由解得:
.
故答案为:,.
乒乓球水平射出后做平抛运动,而平抛运动的加速度不变,做匀变速曲线运动,根据高度求出平抛运动的时间,结合水平位移求出发射的初速度.
解决本题的关键是要掌握平抛运动在水平方向和竖直方向上的运动规律,抓住等时性进行分析求解.
13.【答案】解:根据得,小球在空中运动的时间.
设小球运动到墙顶点所用时间为
竖直方向上有:,
水平方向上有:
代入数据解得
最小时,小球恰好经过墙顶点后落在马路上,最大时,小球落在马路的最右端.
设的最大值为
竖直方向上有:
水平方向上有:
代入数据解得
所以小球抛出时的速度取值范围大小为 .
答:小球在空中运动的时间为;
小球离开房顶时的速度为;
小球离开房顶时的速度的取值范围为 .
【解析】根据高度出小球在空中运动的时间.
根据下降的高度求出平抛运动的时间,结合水平位移和时间求出小球离开房顶的速度.
抓住小球刚好经过墙顶以及小球刚好不落在马路上,结合两个临界状态,根据平抛运动的规律求出小球离开房顶的初速度取值范围.
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界状态,结合运动学公式灵活求解,难度不大.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、单选题(本大题共10小题,共60.0分)
生活中曲线运动随处可见,关于物体做曲线运动,下列说法正确的是( )
A. 速度方向有时与曲线相切,有时与曲线的切线垂直
B. 平抛运动是匀变速曲线运动,斜抛运动是变加速曲线运动
C. 物体所受合力方向一定指向曲线的凹侧
D. 物体所受合力可能不变,但它的加速度一定改变
若已知物体运动的初速度的方向及它受到的恒定的合力的方向,如图所示,则物体运动的轨迹可能是 ( )
A. B. C. D.
一个做平抛运动的物体,初速度为,经过一段时间,它的末速度与竖直方向的夹角为,重力加速度取,则它下落的时间约为 ( )
A. B. C. D.
利用手机可以玩一种叫“扔纸团”的小游戏。如图所示,游戏时,游戏者滑动屏幕将纸团从点以速度水抛向固定在水平地面上的圆柱形废纸篓,纸团恰好从纸篓的上边沿入篓并直接打在纸篓的底角。若要让纸团进入纸篓中并直接击中篓底正中间,下列做法可行的是( )
A. 在点将纸团以小于的速度水平抛出
B. 在点将纸团以大于的速度水平抛出
C. 在点正上方某位置将纸团以小于的速度水平抛出
D. 在点正下方某位置将纸团以大于的速度水平抛出
如图所示,、两物体以相同的水平速度从坐标系原点沿轴正方向被抛出,在竖直平面内运动,落地点为;紧贴光滑的斜面运动,落地点为,和对应的坐标分别为和,不计空气阻力,下列说法正确的是( )
A. 落在点时恰好落在点 B. 先到达点
C. D.
如图所示,是长方形对角线的交点,是底边的中点,、、处的三个小球分别沿图示方向做平抛运动,下列表述不正确的是( )
A. 若、、处三球同时抛出,三球不可能在落地前相遇
B. 要、处两球在空中相遇,则球必须先抛出
C. 若、处两球能在地面相遇,则、在空中运动的时间之比为:
D. 若、处两球在点相遇,则一定满足
如图所示,小船以大小为、方向与上游河岸成的速度在静水中的速度从处过河,经过时间正好到达正对岸的处。现要使小船在更短的时间内过河并且也正好到达正对岸处,在水流速度不变的情况下,可采取下列方法中的哪一种( )
A. 只要增大大小,不必改变角 B. 只要增大角,不必改变大小
C. 在增大的同时,也必须适当增大角 D. 在增大的同时,也必须适当减小角
倾角为的斜面,长为,在顶端水平抛出一个小球,小球刚好落在斜面的底端,如图所示,那么小球的初速度的大小是重力加速度为( )
A. B. C. D.
在年世界田径锦标赛男子跳远决赛中,岁的中国选手王嘉男凭借最后一跳米的成绩逆风翻盘,夺得中国田径史上首枚世锦赛跳远金牌。这不仅是中国男子田赛项目的历史性突破,也是亚洲运动员第一次登上世锦赛跳远冠军的宝座。某同学在校运会上参加跳远比赛,他腾空过程中离地面的最大高度,成绩为,该同学落入沙坑瞬间速度方向与水平面的夹角为,将该同学视为质点,不计空气阻力,则有
A. B. C. D.
如图所示,在竖直放置的半圆形容器的中心点分别以水平初速度、向左、右抛出两个小球可视为质点,最终它们分别落在容器上的点和点,已知与互相垂直,且与竖直方向成角,则两小球初速度之比为( )
A. B. C. D.
二、实验题(本大题共2小题,共28.0分)
某探究小组在居家学习期间,利用手机相机的连拍功能拍照时间间隔相同对“斜抛运动的特点”进行了自主探究。小球被斜向上抛出后,某段运动过程的连拍照片经叠加处理后如图所示。图中水平线与竖直线分别等距,数字为小球在图片中各位置的序号,仅由图片中信息可知:
图片显示的各位置中,是否存在小球运动过程中的最高点?______选填“是”或“否”;
小球在水平方向的分运动为______运动;
图片中能证明小球在竖直方向做匀变速直线运动的信息是_______________。
如图所示是乒乓球发射器示意图,发射口距桌面高度为,假定乒乓球水平射出,落在桌面上与发射口水平距离为的点,飞行过程中未触网,不计空气阻力,取,则球从发射口到桌面的时间为______球从发射口射出的速率为______ .
三、计算题(本大题共1小题,共12.0分)
如图所示,水平屋顶高,墙高,墙到房子的距离,墙外马路宽,小球从房顶点水平飞出,取
若小球落在墙外的马路上,求小球在空中运动的时间;
若小球恰好经过墙顶点后落在马路上,求小球离开房顶时的速度;
若小球落在墙外的马路上,求小球离开房顶时的速度的取值范围。
答案和解析
1.【答案】
【解析】
【分析】
本题考查了物体做曲线运动;解决本题的关键知道合运动是直线运动还是曲线运动取决于合速度方向与合加速度方向是否在同一条直线上,以及会根据平行四边形定则判断合速度与分速度的大小关系。
曲线运动的条件,合外力与速度不在一条直线上,速度方向时刻变化,故曲线运动一定是变速运动,曲线运动的速度的方向与该点曲线的切线方向相同;
平抛运动、斜抛运动的加速度不变,均做匀变速曲线运动,速度均匀变化;
物体做曲线运动的加速度的方向指向曲线的凹侧;
在恒力作用下,物体可以做曲线运动。
【解答】
A.在曲线运动中,质点的速度方向一定沿着轨迹的切线方向,故A错误;
B.平抛运动是匀变速曲线运动,斜抛运动也是匀变速曲线运动,故B错误;
C.根据曲线运动的受力特点可知,做曲线运动的物体其所受合力一定指向轨迹的凹侧,故C正确;
D.做曲线运动的物体可以受恒力作用,其加速度可以保持不变,如平抛运动,故D错误。
故选。
2.【答案】
【解析】
【分析】本题考查物体做曲线运动的条件,做曲线运动的物体,速度方向沿着曲线上该点的切线方向,合力的方向与速度方向不共线,且指向曲线的凹侧,运动轨迹在合力与速度之间。
【解答】
物体做曲线运动时,速度沿曲线的切线方向,合力方向和速度方向不共线,且指向曲线的凹侧,则运动轨迹在合力与速度之间,且向合力的方向弯曲,故B正确,ACD错误。
3.【答案】
【解析】解:
物体做平抛运动,根据题意,结合平抛运动的特点可知,解得,故ABC错误,D正确.
4.【答案】
【解析】
【分析】
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合运动学公式分析判断。
本题运用平抛运动的知识分析处理生活中的问题,比较简单,关键运用运动的分解方法得到水平位移的表达式。
【解答】
A.在点的初速度减小,则下降到框上沿这段时间内,水平位移变小,则小球不能进入筐中,故A错误。
B.在点的初速度增大,则下降到筐底的时间内,水平位移增大,不能直接击中筐底的正中间,故B错误。
C.在点正上方某位置将小球以小于的速度水平抛出,根据知,水平位移可以减小,也不会与框的左边沿相撞,落在筐底的正中间,故C正确。
D.在点正下方某位置将小球以大于的速度水平抛出,则小球能进筐,但不能击中篓底正中间。故D错误。
故选C。
5.【答案】
【解析】
【分析】
小球做平抛运动,小球做类平抛运动,根据牛顿第二定律求出在斜面上的加速度,结合下落的高度和沿斜面下落的位移,求出运动的时间,进行比较.通过初速度和运动的时间比较沿轴方向上的位移。
解决本题的关键掌握处理类平抛运动的方法,通过水平方向和沿斜面向下方向的规律进行分析求解。
【解答】
对于球,运动的时间为:,,
对于球,,根据,解得:,
可知,,.
沿轴方向上的位移为:,知故ABC错误,D正确。
6.【答案】
【解析】解:若、、处三球同时抛出,竖直分运动均是自由落体运动,故处、处的小球不可能与处小球相遇,故A正确;
B.由于平抛运动的竖直分运动是自由落体运动,要、处两球在空中相遇,则球必须先抛出,故B正确;
C.若、处两球能在地面相遇,根据可知,两个球运动时间之比为:,故C错误;
D.若、处两球在点相遇,由于水平分运动是匀速直线运动,水平分位移相等,时间也相等,故水平分速度相等,即初速度相等,则一定满足,故D正确。
本题选择不正确的,
故选:。
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据高度比较运动的时间,结合水平位移和时间比较初速度。
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道运动的时间由高度决定,初速度和时间共同决定水平位移。
7.【答案】
【解析】
【分析】
由题意可知,小船在更短的时间内过河并且也正好到达正对岸处,则船在水流方向的分速度不变,船在垂直河岸方向的分速度要增大,根据平行四边形定则,即可求解。
考查运动的合成与分解,掌握平行四边形定则的应用,注意要使小船在更短的时间内过河并且也正好到达正对岸处,必须满足船在水流方向的分速度不变,且垂直河岸的分速度要增大。
【解答】
A.若只增大大小,不必改变角,则船在水流方向的分速度增大,因此船不可能垂直达到对岸,故A错误;
B.若只增大角,不必改变大小,同理可知,水流方向的分速度在减小,而垂直河岸的分速度在增大,船不可能垂直到达对岸,故B错误;
C.若在增大的同时,也必须适当增大角,这样才能保证水流方向的分速度不变,而垂直河岸的分速度在增大,则船还能垂直达到对岸,且时间更短,故C正确;
D.若增大的同时,也必须适当减小角,则水流方向的分速度增大,不能垂直到达对岸,故D错误。
故选C。
8.【答案】
【解析】
【分析】解决本题的关键关键知道平抛运动在水平方向和竖直方向上的运动规律,知道平抛运动的时间由高度决定,初速度和时间共同决定水平位移。
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据下落的高度求出运动的时间,再根据水平位移和时间求出小球的初速度。
【解答】
在竖直方向上有:,解得,
则初速度,故A正确,BCD错误,故选:。
9.【答案】
【解析】
【分析】
根据平抛运动的推论进行求解即可。
本题考查抛体运动的处理规律,掌握运动的合成与分解的应用,要注意运动员在水平方向做匀速直线运动,从最高点向下竖直方向做自由落体运动。
【解答】
运动员从最高点到落地的过程做平抛运动,根据平抛运动的推论,速度的反向延长线过
水平位移的中点,则有:,故ABC错误;D正确。
故选D。
10.【答案】
【解析】
【分析】
平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据平抛运动水平位移和竖直位移的关系确定两小球运动时间之比和初速度大小之比。
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住两球竖直位移和水平位移之间的关系,运用运动学公式研究。
【解答】
由几何关系可知:左小球下降的竖直高度为,右小球下降的竖直高度为
由平抛运动规律可知:;
由此可得:时间之比
由几何关系可知:两小球水平运动的位移分别为:
,
由平抛运动规律可知:,,
由此可得:两小球的初速度之比为,故ABD错误,C正确。
故选C。
11.【答案】否;匀速直线;
任意连续相等时间内的竖直位移差相等。
【解析】
【分析】
本题考查了对斜抛运动的认识。
最高点速度方向应是水平方向;
根据相连点的水平间距解答;
根据匀变速直线运动的推论和竖直方向的位移差分析。
【解答】
最高点速度方向应是水平方向,用平滑的曲线连接图中各点,如图:
各点的速度方向均不是水平,所以图片显示的各位置中不存在小球运动过程中的最高点;
相邻位置之间的水平间距相等,且拍照时间间隔相同,所以小球在水平方向的分运动为匀速直线运动;
观察图片可知:任意连续相等时间内的竖直位移差相等,所以图片中能证明小球在竖直方向做匀变速直线运动。
12.【答案】
【解析】解:乒乓球水平射出后做平抛运动,其加速度等于重力加速度,始终保持不变,由得:
;
由解得:
.
故答案为:,.
乒乓球水平射出后做平抛运动,而平抛运动的加速度不变,做匀变速曲线运动,根据高度求出平抛运动的时间,结合水平位移求出发射的初速度.
解决本题的关键是要掌握平抛运动在水平方向和竖直方向上的运动规律,抓住等时性进行分析求解.
13.【答案】解:根据得,小球在空中运动的时间.
设小球运动到墙顶点所用时间为
竖直方向上有:,
水平方向上有:
代入数据解得
最小时,小球恰好经过墙顶点后落在马路上,最大时,小球落在马路的最右端.
设的最大值为
竖直方向上有:
水平方向上有:
代入数据解得
所以小球抛出时的速度取值范围大小为 .
答:小球在空中运动的时间为;
小球离开房顶时的速度为;
小球离开房顶时的速度的取值范围为 .
【解析】根据高度出小球在空中运动的时间.
根据下降的高度求出平抛运动的时间,结合水平位移和时间求出小球离开房顶的速度.
抓住小球刚好经过墙顶以及小球刚好不落在马路上,结合两个临界状态,根据平抛运动的规律求出小球离开房顶的初速度取值范围.
解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,抓住临界状态,结合运动学公式灵活求解,难度不大.
第1页,共1页
