北师大版九年级数学下册2.4.1 二次函数的应用 最大面积问题 课时作业(含答案)
文档属性
| 名称 | 北师大版九年级数学下册2.4.1 二次函数的应用 最大面积问题 课时作业(含答案) | 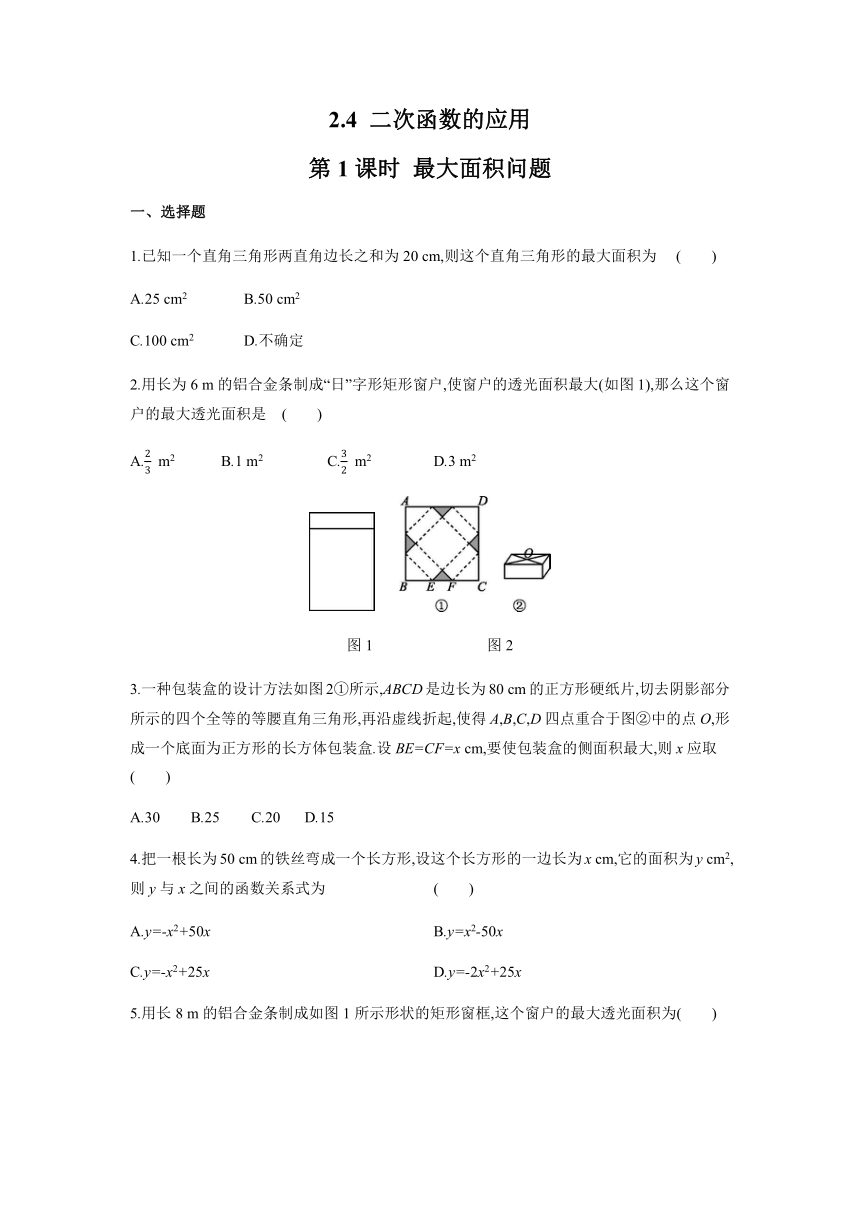 | |
| 格式 | zip | ||
| 文件大小 | 101.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 13:32:04 | ||
图片预览


文档简介
2.4 二次函数的应用
第1课时 最大面积问题
一、选择题
1.已知一个直角三角形两直角边长之和为20 cm,则这个直角三角形的最大面积为 ( )
A.25 cm2 B.50 cm2
C.100 cm2 D.不确定
2.用长为6 m的铝合金条制成“日”字形矩形窗户,使窗户的透光面积最大(如图1),那么这个窗户的最大透光面积是 ( )
A. m2 B.1 m2 C. m2 D.3 m2
图1 图2
3.一种包装盒的设计方法如图2①所示,ABCD是边长为80 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图②中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=x cm,要使包装盒的侧面积最大,则x应取( )
A.30 B.25 C.20 D.15
4.把一根长为50 cm的铁丝弯成一个长方形,设这个长方形的一边长为x cm,它的面积为y cm2,则y与x之间的函数关系式为 ( )
A.y=-x2+50x B.y=x2-50x
C.y=-x2+25x D.y=-2x2+25x
5.用长8 m的铝合金条制成如图1所示形状的矩形窗框,这个窗户的最大透光面积为( )
图1
A. m2 B. m2 C. m2 D.4 m2
6 如图以40 m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t-5t2.下列叙述正确的是 ( )
A.小球的飞行高度不能达到15 m
B.小球的飞行高度可以达到25 m
C.小球从飞出到落地要用时4 s
D.小球飞出1 s时的飞行高度为10 m
二、填空题
7.某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50 m),中间用两道墙隔开(如图2).已知计划中的建筑材料可建墙的总长度为48 m,则这三间长方形种牛饲养室的总占地面积的最大值为 m2.
图2
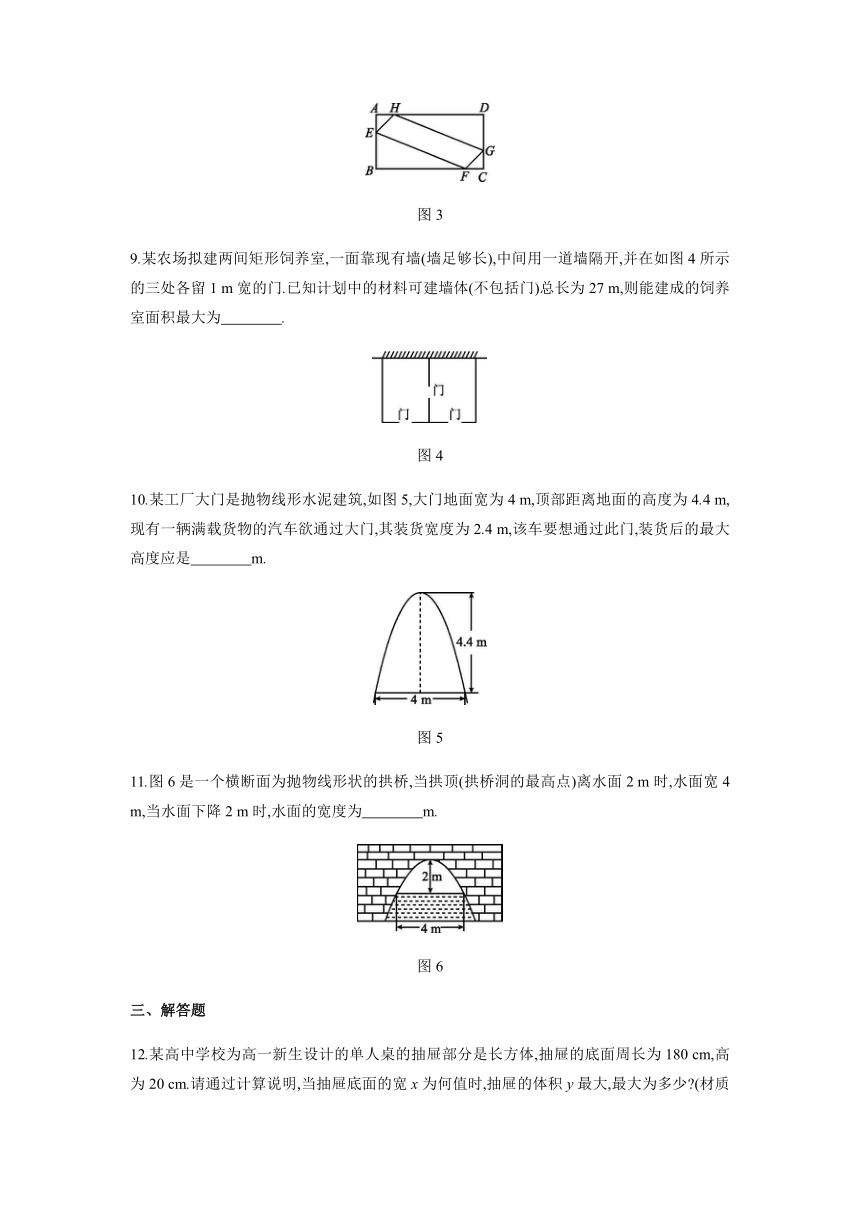
8.如图3,为了美化校园环境,某中学准备在一块空地(长方形ABCD,AB=10 m,BC=20 m)上进行绿化,中间的一块(图中四边形EFGH)上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求AE=AH=CF=CG,当四边形EFGH(中间种花的一块)面积最大时,AE=
m.
图3
9.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图4所示的三处各留1 m宽的门.已知计划中的材料可建墙体(不包括门)总长为27 m,则能建成的饲养室面积最大为 .
图4
10.某工厂大门是抛物线形水泥建筑,如图5,大门地面宽为4 m,顶部距离地面的高度为4.4 m,现有一辆满载货物的汽车欲通过大门,其装货宽度为2.4 m,该车要想通过此门,装货后的最大高度应是 m.
图5
11.图6是一个横断面为抛物线形状的拱桥,当拱顶(拱桥洞的最高点)离水面2 m时,水面宽4 m,当水面下降2 m时,水面的宽度为 m.
图6
三、解答题
12.某高中学校为高一新生设计的单人桌的抽屉部分是长方体,抽屉的底面周长为180 cm,高为20 cm.请通过计算说明,当抽屉底面的宽x为何值时,抽屉的体积y最大,最大为多少 (材质及其厚度等忽略不计)
13在美化校园的活动中,某兴趣小组想借助如图7所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.
(1)若花园的面积为192 m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
图7
14.如图8,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,点E,F分别在AB,AC上,AD交EF于点H.
(1)求证:=;
(2)设EF=x,则当x为何值时,矩形EFPQ的面积最大 请求出其最大面积.
图8
参考答案
1.B 2.C 3.C 4.C 5.C 6.C.
7.144
8.7.5
9.75 m2
10.2.816
11 4 .
12.解:因为长方体抽屉的底面宽为x cm,则长为(90-x)cm.
由题意可列不等式组解得0根据题意,得y=20x(90-x).
整理,得y=-20x2+1800x=-20(x-45)2+40500.
∵a=-20<0,0∴当x=45时,y取得最大值,y最大=40500,
即当抽屉底面的宽为45 cm时,抽屉的体积最大,最大为40500 cm3.
13.解:(1)∵AB=x m,
∴BC=(28-x)m,
∴x(28-x)=192,解得x1=12,x2=16.
则x的值为12或16.
(2)由题意,得S=x(28-x)=-x2+28x=-(x-14)2+196.
∵在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,
∴解得6≤x≤13,
∴当x=13时,S取得最大值,此时S=-(13-14)2+196=195.
因此,花园面积S的最大值为195 m2.
14.解:(1)证明:∵在矩形EFPQ中,EF∥PQ,
∴∠AEF=∠B,∠AFE=∠C,
∴△AEF∽△ABC.
∵AD⊥BC,EF∥PQ,
∴AH⊥EF,
∴=.
(2)设矩形EFPQ的面积为y.
∵=,
∴=,
∴AH=x,
∴DH=4-x,
∴y=-x2+4x=-(x-)2+5(0又∵a=-<0,
∴当x=时,y有最大值5.
即当x=时,矩形EFPQ的面积最大,最大面积为5.
第1课时 最大面积问题
一、选择题
1.已知一个直角三角形两直角边长之和为20 cm,则这个直角三角形的最大面积为 ( )
A.25 cm2 B.50 cm2
C.100 cm2 D.不确定
2.用长为6 m的铝合金条制成“日”字形矩形窗户,使窗户的透光面积最大(如图1),那么这个窗户的最大透光面积是 ( )
A. m2 B.1 m2 C. m2 D.3 m2
图1 图2
3.一种包装盒的设计方法如图2①所示,ABCD是边长为80 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图②中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=x cm,要使包装盒的侧面积最大,则x应取( )
A.30 B.25 C.20 D.15
4.把一根长为50 cm的铁丝弯成一个长方形,设这个长方形的一边长为x cm,它的面积为y cm2,则y与x之间的函数关系式为 ( )
A.y=-x2+50x B.y=x2-50x
C.y=-x2+25x D.y=-2x2+25x
5.用长8 m的铝合金条制成如图1所示形状的矩形窗框,这个窗户的最大透光面积为( )
图1
A. m2 B. m2 C. m2 D.4 m2
6 如图以40 m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t-5t2.下列叙述正确的是 ( )
A.小球的飞行高度不能达到15 m
B.小球的飞行高度可以达到25 m
C.小球从飞出到落地要用时4 s
D.小球飞出1 s时的飞行高度为10 m
二、填空题
7.某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长50 m),中间用两道墙隔开(如图2).已知计划中的建筑材料可建墙的总长度为48 m,则这三间长方形种牛饲养室的总占地面积的最大值为 m2.
图2
8.如图3,为了美化校园环境,某中学准备在一块空地(长方形ABCD,AB=10 m,BC=20 m)上进行绿化,中间的一块(图中四边形EFGH)上种花,其他的四块(图中的四个直角三角形)上铺设草坪,并要求AE=AH=CF=CG,当四边形EFGH(中间种花的一块)面积最大时,AE=
m.
图3
9.某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图4所示的三处各留1 m宽的门.已知计划中的材料可建墙体(不包括门)总长为27 m,则能建成的饲养室面积最大为 .
图4
10.某工厂大门是抛物线形水泥建筑,如图5,大门地面宽为4 m,顶部距离地面的高度为4.4 m,现有一辆满载货物的汽车欲通过大门,其装货宽度为2.4 m,该车要想通过此门,装货后的最大高度应是 m.
图5
11.图6是一个横断面为抛物线形状的拱桥,当拱顶(拱桥洞的最高点)离水面2 m时,水面宽4 m,当水面下降2 m时,水面的宽度为 m.
图6
三、解答题
12.某高中学校为高一新生设计的单人桌的抽屉部分是长方体,抽屉的底面周长为180 cm,高为20 cm.请通过计算说明,当抽屉底面的宽x为何值时,抽屉的体积y最大,最大为多少 (材质及其厚度等忽略不计)
13在美化校园的活动中,某兴趣小组想借助如图7所示的直角墙角(两边足够长),用28 m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x m.
(1)若花园的面积为192 m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
图7
14.如图8,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,点E,F分别在AB,AC上,AD交EF于点H.
(1)求证:=;
(2)设EF=x,则当x为何值时,矩形EFPQ的面积最大 请求出其最大面积.
图8
参考答案
1.B 2.C 3.C 4.C 5.C 6.C.
7.144
8.7.5
9.75 m2
10.2.816
11 4 .
12.解:因为长方体抽屉的底面宽为x cm,则长为(90-x)cm.
由题意可列不等式组解得0
整理,得y=-20x2+1800x=-20(x-45)2+40500.
∵a=-20<0,0
即当抽屉底面的宽为45 cm时,抽屉的体积最大,最大为40500 cm3.
13.解:(1)∵AB=x m,
∴BC=(28-x)m,
∴x(28-x)=192,解得x1=12,x2=16.
则x的值为12或16.
(2)由题意,得S=x(28-x)=-x2+28x=-(x-14)2+196.
∵在P处有一棵树与墙CD,AD的距离分别是15 m和6 m,
∴解得6≤x≤13,
∴当x=13时,S取得最大值,此时S=-(13-14)2+196=195.
因此,花园面积S的最大值为195 m2.
14.解:(1)证明:∵在矩形EFPQ中,EF∥PQ,
∴∠AEF=∠B,∠AFE=∠C,
∴△AEF∽△ABC.
∵AD⊥BC,EF∥PQ,
∴AH⊥EF,
∴=.
(2)设矩形EFPQ的面积为y.
∵=,
∴=,
∴AH=x,
∴DH=4-x,
∴y=-x2+4x=-(x-)2+5(0
∴当x=时,y有最大值5.
即当x=时,矩形EFPQ的面积最大,最大面积为5.
