人教A版(2019)高中数学选择性必修第一册 《直线与圆的位置关系》名师课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 《直线与圆的位置关系》名师课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 00:00:00 | ||
图片预览









文档简介
(共37张PPT)
复习引入
1.直线的一般式方程是_______________________
2.圆的标准方程是_______________________
其中圆心坐标为____________ 半径为 ___________
3.圆的一般方程为_________________________________
其中圆心坐标为____________ 半径为 ____________
A+B+C=0(A,B不同时为0)
(a,b)
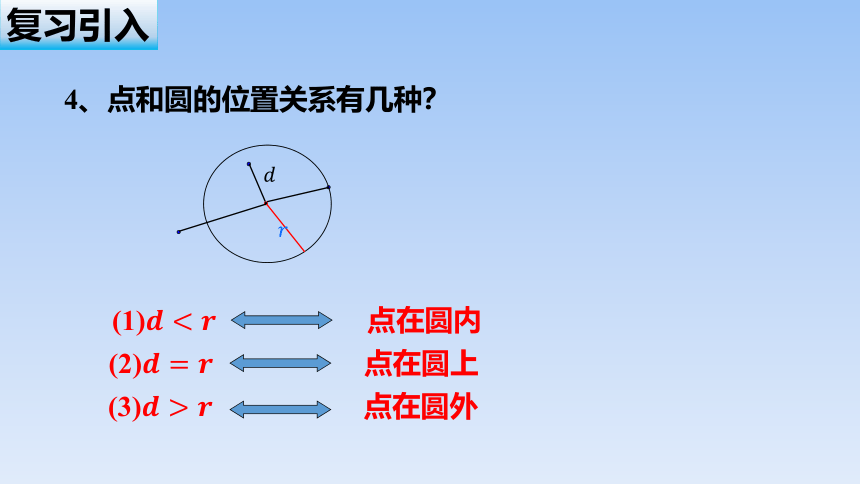
4、点和圆的位置关系有几种?
复习引入
(1) 点在圆内
(2) 点在圆上
(3) 点在圆外
人教A版同步教材名师课件
直线与圆的位置关系
学习目标
学 习 目 标 核心素养
直线与圆的位置关系 数学抽象
数学运算
直线与圆的方程的应用 数学抽象
数学建模
学习目标
学习目标:
1.掌握直线与圆的三种位置关系:相交、相切、相离.
2.会用代数法和几何法来判断直线与圆的三种位置关系.
3.会用直线与圆的位置关系解决一些实际问题.
学科核心素养:
通过研究直线与圆的位置关系,提升逻辑推理、数学运算、直观想象的数学素养.
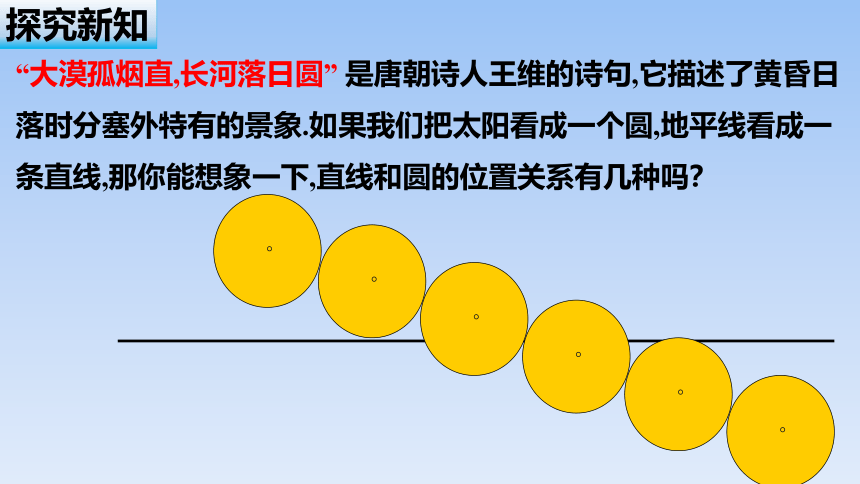
“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象.如果我们把太阳看成一个圆,地平线看成一条直线,那你能想象一下,直线和圆的位置关系有几种吗?
探究新知
直线与圆相交
直线与圆相切
直线与圆相离
位置关系
判别方法
2个交点
1个交点
没有交点
问题:如何用直线和圆的方程判断它们之间的位置关系?
探究新知
直线与圆的位置关系
(1) 利用直线与圆的公共点的个数进行判断:
n=0
n=1
n=2
直线与圆相离
直线与圆相切
直线与圆相交
探究新知
代数法
直线与圆的位置关系的判定方法
设方程组的解的个数为n
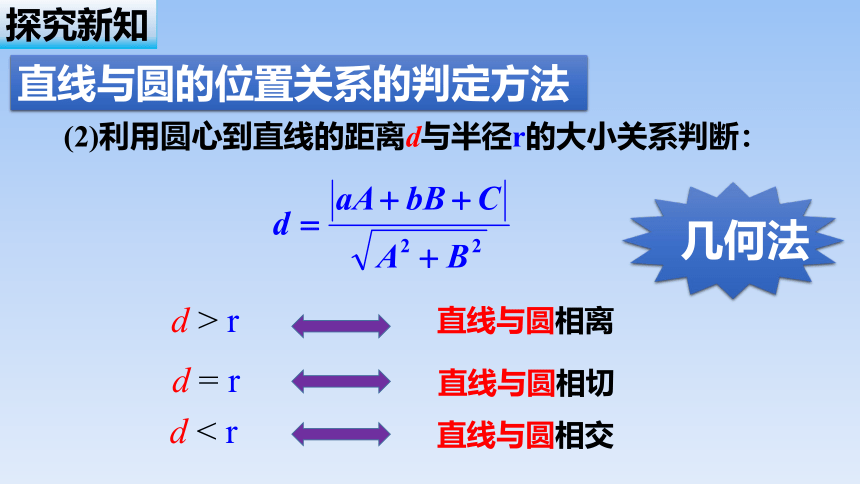
(2)利用圆心到直线的距离d与半径r的大小关系判断:
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
几何法
探究新知
直线与圆的位置关系的判定方法
.
O
C
A
B
l
(1)法一
∴其圆心 ( , ),半径长为,
所以,直线 与圆相交,有两个公共点.
典例讲解
解析
例1、如图,已知直线 :和圆心为C的圆0,判断直线 与圆的位置关系;如果相交,求它们的交点坐标.
.
O
C
A
B
l
典例讲解
解析
例1、如图,已知直线 :和圆心为C的圆0,判断直线 与圆的位置关系;如果相交,求它们的交点坐标.
(1)法二
由直线 与圆的方程,得
消去,得
∴直线 与圆相交,有两个公共点.
.
O
C
A
B
l
典例讲解
解析
例1、如图,已知直线 :和圆心为C的圆0,判断直线 与圆的位置关系;如果相交,求它们的交点坐标.
(2)由, ,
把代入方程,得,
把代入方程,得,
所以,直线 与圆有两个公共点,
它们的坐标分别是, .
方法归纳
几何法判定直线与圆的位置关系的主要步骤是:
①把圆的方程化为标准方程,求出圆心和半径.
②利用点到直线的距离公式求圆心到直线的距离.
③判断:
当时,直线与圆相离;
当时,直线与圆相切;
当时,直线与圆相交.
代数法判定直线与圆的位置关系的主要步骤是:
1.将直线方程与圆方程联立成方程组;
2.通过消元,得到一个一元二次方程;
3.求出其判别式的值;
4.比较与0的大小关系:
若,则直线与圆相交;
若,则直线与圆相切;
若,则直线与圆相离.
方法归纳
1、直线与圆的位置关系是( )
A.相离 B.相切 C.相交且过圆心 D.相交不过圆心
将圆的方程配方得
圆心.
∴直线与圆相交且通过圆心.
C
变式训练
解析
2、以点为圆心的圆与直线相离,则圆的半径r的取值范围是____________.
圆心到直线的距离, ∴ .
3、若直线与圆相交,则点的位置是( )
A.在圆上 B.在圆外 C.在圆内 D.以上都有可能
B
由题意可得,∴,∴点在圆外.
变式训练
解析
解析
典例讲解
法一:直线和圆的公共点坐标就是方程组的解.
解这个方程组,得所以公共点的坐标为,,
所以,直线被圆截得的弦长为.
解析
例2、求直线被圆截得的弦长.
典例讲解
解析
例2、求直线被圆截得的弦长.
弦得中点为,则(为坐标原点),
所以
所以
法二:如图,设直线与圆交于两点,
O
M
.
E
F
因为直线过点M,可设所求直线的方程为:,即:,
对于圆:,
如图:.
, ,
.
所求直线为:
T
典例讲解
例3、已知过点的直线被圆截得的弦长为,求直线的方程.
解析
弦长问题
(1)代数法:解方程组求交点,两点间的距离公式求弦长
(2)几何法:圆心到直线的距离和勾股定理求弦长(常用)
弦长公式为
A
B
O
(注:我们把称为弦心距.)
方法归纳
设点的坐标分别为, 由,得
即①
又, 是方程组的实数解,
即是方程②的两个根,
所以 ③
变式训练
解析
4.已知圆与直线相交于两点,O为原点,且OP⊥OQ,求实数m的值.
变式训练
解析
因为在直线上,
所以
将③代入,得. ④
将③④代入①,解得.代入方程②,检验成立,所以
4.已知圆与直线相交于两点,O为原点,且OP⊥OQ,求实数m的值.
典例讲解
例5、下图是某圆拱形桥一孔圆拱的示意图.这个圆的圆拱跨度,拱高,建造时每间隔4m需要用一根支柱支撑,求支柱的高度(精确到0.01m).
设圆的方程为:
得解得
把圆的方程为把点横坐标代入可得
答:支柱的高度约为3.86m.
解析
建立如图所示的直角坐标系,则P都在圆上.
利用坐标法解决几何问题的步骤是:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
方法归纳
设,即.则圆心(2,0)到直线的距离为半径时直线与圆相切,斜率取得最大、最小值.由 ∴
典例讲解
解析
例6、已知实数、满足方程求:(1) 的最值;(2)的最值;(3) 的最值.
(1)如图,方程表示以点(2,0)为圆心,以为半径的圆.
(也可由平面几何知识,得OC=2,CP= ,∠POC=60°,直线OP的倾斜角为60°,直线的倾斜角为120°)
典例讲解
解析
例6、已知实数、满足方程求:(1) 的最值;(2)的最值;(3) 的最值.
(2)设,则,
仅当直线与圆切于第四象限时,
截距b取最小值,切于第一象限时,截距b取最大值.
由点到直线的距离公式,得
即
故.
又因为圆心到原点的距离为
所以的最大值是
所以的最小值是.
典例讲解
解析
例6、已知实数、满足方程求:(1) 的最值;(2)的最值;(3) 的最值.
(3)表示圆上的一点与原点距离的平方,由平面几何知识知,在原点和圆心连线与圆的两个交点处取得最大值和最小值,
如图点的坐标为(2-,0),点的坐标为(2+,0).
与圆上点有关代数式的最值的常见类型及解法.
①形如型的最值问题,可转化为过点和点的直线的斜率的最值问题;
②形如t=ax+by型的最值问题,可转化为动直线的截距的最值问题;
③形如(x-a)2+(y-b)2型的最值问题,可转化为动点到定点的距离平方的最值问题.
方法归纳
变式训练
5.已知实数、满足方程
求:(1) 的最值;(2)的最值.
令,则表示圆上一点与的斜率,
∴.
由题意可知当直线kx-y+2k+3=0与圆相切时k取最值.
∴ ,
解析
(2)令, 即,当直线与圆C相切时b取最值.∴ , ∴,
1、直线与圆相交求交点坐标,只需联立两方程求解二元二次方程组即可
①求出交点坐标,利用两点间距离公式,求出弦长.
2、直线与圆相交时弦长的求法
素养提炼
②利用弦长公式求:
其中为交点的横坐标,k为已知直线斜率.
③设弦长为,弦心距为d,半径为r,则有,
即半弦长、弦心距、半径构成直角三角形,数形结合,利用勾股定理求解.
当堂练习
圆心坐标为(1,-1),圆心到直线的距离为 又点(1,-1)不在直线上,所以直线与圆相交且不过圆心.选D.
1.直线与圆的位置关系是( )
A.过圆心 B.相切 C.相离 D.相交但不过圆心
D
解析
2.过点P(0,1)的直线与圆相交于A,B两点,若,则该直线的斜率为( )
A. B. C. D.
由题意设直线的方程为,因为圆的圆心为(1,1),半径为r=1,又弦长,所以圆心到直线的距离为
所以有解得k= .
解析
A
当堂练习
设圆心到直线的距离为,则.由直线与圆相切可得.
3.若直线与圆相切,则( )
A. B.5 C. D.25
设方程为y-4=k(x+1),即kx-y+k+4=0.∴,∴ ,
解得故的方程为或.
4.过点圆C:的切线的方程为______________________.
或
解析
C
解析
当堂练习
5.已知圆C经过点A(2,0),B(1,),且圆心C在直线上.
(1)求圆C的方程;
(2)过点(1, )的直线截圆所得弦长为,求直线的方程.
(1)的中点坐标( ,), 的斜率为.可得垂直平分线方程为,与的交点为圆心坐标,半径为2,所以圆C的方程为.
(2)直线的斜率存在时,设直线的斜率为k,又直线过(,),
∴直线的方程为,即.
则圆心到直线的距离,又圆的半径r=2,截得的弦长为,
解析
当堂练习
5.已知圆C经过点A(2,0),B(1,),且圆心C在直线上.
(1)求圆C的方程;
(2)过点(1, )的直线截圆所得弦长为,求直线的方程.
解析
则有,解得: ,
则直线的方程为.
当直线的斜率不存在时,直线方程为,满足题意.
∴直线的方程为或.
1.判断直线与圆的位置关系有两种方法
图形
位置关系
相交
相切
相离
交点个数
2个
1个
0个
d与r关系
dd=r
d>r
归纳小结
2.弦长问题
(1)代数法:解方程组求交点,两点间的距离公式求弦长
(2)几何法:圆心到直线的距离和勾股定理求弦长(常用)
A
B
O
(注:我们把称为弦心距.)
归纳小结
弦长公式为
P98 习题2.5:2、3、4
作 业
复习引入
1.直线的一般式方程是_______________________
2.圆的标准方程是_______________________
其中圆心坐标为____________ 半径为 ___________
3.圆的一般方程为_________________________________
其中圆心坐标为____________ 半径为 ____________
A+B+C=0(A,B不同时为0)
(a,b)
4、点和圆的位置关系有几种?
复习引入
(1) 点在圆内
(2) 点在圆上
(3) 点在圆外
人教A版同步教材名师课件
直线与圆的位置关系
学习目标
学 习 目 标 核心素养
直线与圆的位置关系 数学抽象
数学运算
直线与圆的方程的应用 数学抽象
数学建模
学习目标
学习目标:
1.掌握直线与圆的三种位置关系:相交、相切、相离.
2.会用代数法和几何法来判断直线与圆的三种位置关系.
3.会用直线与圆的位置关系解决一些实际问题.
学科核心素养:
通过研究直线与圆的位置关系,提升逻辑推理、数学运算、直观想象的数学素养.
“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象.如果我们把太阳看成一个圆,地平线看成一条直线,那你能想象一下,直线和圆的位置关系有几种吗?
探究新知
直线与圆相交
直线与圆相切
直线与圆相离
位置关系
判别方法
2个交点
1个交点
没有交点
问题:如何用直线和圆的方程判断它们之间的位置关系?
探究新知
直线与圆的位置关系
(1) 利用直线与圆的公共点的个数进行判断:
n=0
n=1
n=2
直线与圆相离
直线与圆相切
直线与圆相交
探究新知
代数法
直线与圆的位置关系的判定方法
设方程组的解的个数为n
(2)利用圆心到直线的距离d与半径r的大小关系判断:
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
几何法
探究新知
直线与圆的位置关系的判定方法
.
O
C
A
B
l
(1)法一
∴其圆心 ( , ),半径长为,
所以,直线 与圆相交,有两个公共点.
典例讲解
解析
例1、如图,已知直线 :和圆心为C的圆0,判断直线 与圆的位置关系;如果相交,求它们的交点坐标.
.
O
C
A
B
l
典例讲解
解析
例1、如图,已知直线 :和圆心为C的圆0,判断直线 与圆的位置关系;如果相交,求它们的交点坐标.
(1)法二
由直线 与圆的方程,得
消去,得
∴直线 与圆相交,有两个公共点.
.
O
C
A
B
l
典例讲解
解析
例1、如图,已知直线 :和圆心为C的圆0,判断直线 与圆的位置关系;如果相交,求它们的交点坐标.
(2)由, ,
把代入方程,得,
把代入方程,得,
所以,直线 与圆有两个公共点,
它们的坐标分别是, .
方法归纳
几何法判定直线与圆的位置关系的主要步骤是:
①把圆的方程化为标准方程,求出圆心和半径.
②利用点到直线的距离公式求圆心到直线的距离.
③判断:
当时,直线与圆相离;
当时,直线与圆相切;
当时,直线与圆相交.
代数法判定直线与圆的位置关系的主要步骤是:
1.将直线方程与圆方程联立成方程组;
2.通过消元,得到一个一元二次方程;
3.求出其判别式的值;
4.比较与0的大小关系:
若,则直线与圆相交;
若,则直线与圆相切;
若,则直线与圆相离.
方法归纳
1、直线与圆的位置关系是( )
A.相离 B.相切 C.相交且过圆心 D.相交不过圆心
将圆的方程配方得
圆心.
∴直线与圆相交且通过圆心.
C
变式训练
解析
2、以点为圆心的圆与直线相离,则圆的半径r的取值范围是____________.
圆心到直线的距离, ∴ .
3、若直线与圆相交,则点的位置是( )
A.在圆上 B.在圆外 C.在圆内 D.以上都有可能
B
由题意可得,∴,∴点在圆外.
变式训练
解析
解析
典例讲解
法一:直线和圆的公共点坐标就是方程组的解.
解这个方程组,得所以公共点的坐标为,,
所以,直线被圆截得的弦长为.
解析
例2、求直线被圆截得的弦长.
典例讲解
解析
例2、求直线被圆截得的弦长.
弦得中点为,则(为坐标原点),
所以
所以
法二:如图,设直线与圆交于两点,
O
M
.
E
F
因为直线过点M,可设所求直线的方程为:,即:,
对于圆:,
如图:.
, ,
.
所求直线为:
T
典例讲解
例3、已知过点的直线被圆截得的弦长为,求直线的方程.
解析
弦长问题
(1)代数法:解方程组求交点,两点间的距离公式求弦长
(2)几何法:圆心到直线的距离和勾股定理求弦长(常用)
弦长公式为
A
B
O
(注:我们把称为弦心距.)
方法归纳
设点的坐标分别为, 由,得
即①
又, 是方程组的实数解,
即是方程②的两个根,
所以 ③
变式训练
解析
4.已知圆与直线相交于两点,O为原点,且OP⊥OQ,求实数m的值.
变式训练
解析
因为在直线上,
所以
将③代入,得. ④
将③④代入①,解得.代入方程②,检验成立,所以
4.已知圆与直线相交于两点,O为原点,且OP⊥OQ,求实数m的值.
典例讲解
例5、下图是某圆拱形桥一孔圆拱的示意图.这个圆的圆拱跨度,拱高,建造时每间隔4m需要用一根支柱支撑,求支柱的高度(精确到0.01m).
设圆的方程为:
得解得
把圆的方程为把点横坐标代入可得
答:支柱的高度约为3.86m.
解析
建立如图所示的直角坐标系,则P都在圆上.
利用坐标法解决几何问题的步骤是:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
方法归纳
设,即.则圆心(2,0)到直线的距离为半径时直线与圆相切,斜率取得最大、最小值.由 ∴
典例讲解
解析
例6、已知实数、满足方程求:(1) 的最值;(2)的最值;(3) 的最值.
(1)如图,方程表示以点(2,0)为圆心,以为半径的圆.
(也可由平面几何知识,得OC=2,CP= ,∠POC=60°,直线OP的倾斜角为60°,直线的倾斜角为120°)
典例讲解
解析
例6、已知实数、满足方程求:(1) 的最值;(2)的最值;(3) 的最值.
(2)设,则,
仅当直线与圆切于第四象限时,
截距b取最小值,切于第一象限时,截距b取最大值.
由点到直线的距离公式,得
即
故.
又因为圆心到原点的距离为
所以的最大值是
所以的最小值是.
典例讲解
解析
例6、已知实数、满足方程求:(1) 的最值;(2)的最值;(3) 的最值.
(3)表示圆上的一点与原点距离的平方,由平面几何知识知,在原点和圆心连线与圆的两个交点处取得最大值和最小值,
如图点的坐标为(2-,0),点的坐标为(2+,0).
与圆上点有关代数式的最值的常见类型及解法.
①形如型的最值问题,可转化为过点和点的直线的斜率的最值问题;
②形如t=ax+by型的最值问题,可转化为动直线的截距的最值问题;
③形如(x-a)2+(y-b)2型的最值问题,可转化为动点到定点的距离平方的最值问题.
方法归纳
变式训练
5.已知实数、满足方程
求:(1) 的最值;(2)的最值.
令,则表示圆上一点与的斜率,
∴.
由题意可知当直线kx-y+2k+3=0与圆相切时k取最值.
∴ ,
解析
(2)令, 即,当直线与圆C相切时b取最值.∴ , ∴,
1、直线与圆相交求交点坐标,只需联立两方程求解二元二次方程组即可
①求出交点坐标,利用两点间距离公式,求出弦长.
2、直线与圆相交时弦长的求法
素养提炼
②利用弦长公式求:
其中为交点的横坐标,k为已知直线斜率.
③设弦长为,弦心距为d,半径为r,则有,
即半弦长、弦心距、半径构成直角三角形,数形结合,利用勾股定理求解.
当堂练习
圆心坐标为(1,-1),圆心到直线的距离为 又点(1,-1)不在直线上,所以直线与圆相交且不过圆心.选D.
1.直线与圆的位置关系是( )
A.过圆心 B.相切 C.相离 D.相交但不过圆心
D
解析
2.过点P(0,1)的直线与圆相交于A,B两点,若,则该直线的斜率为( )
A. B. C. D.
由题意设直线的方程为,因为圆的圆心为(1,1),半径为r=1,又弦长,所以圆心到直线的距离为
所以有解得k= .
解析
A
当堂练习
设圆心到直线的距离为,则.由直线与圆相切可得.
3.若直线与圆相切,则( )
A. B.5 C. D.25
设方程为y-4=k(x+1),即kx-y+k+4=0.∴,∴ ,
解得故的方程为或.
4.过点圆C:的切线的方程为______________________.
或
解析
C
解析
当堂练习
5.已知圆C经过点A(2,0),B(1,),且圆心C在直线上.
(1)求圆C的方程;
(2)过点(1, )的直线截圆所得弦长为,求直线的方程.
(1)的中点坐标( ,), 的斜率为.可得垂直平分线方程为,与的交点为圆心坐标,半径为2,所以圆C的方程为.
(2)直线的斜率存在时,设直线的斜率为k,又直线过(,),
∴直线的方程为,即.
则圆心到直线的距离,又圆的半径r=2,截得的弦长为,
解析
当堂练习
5.已知圆C经过点A(2,0),B(1,),且圆心C在直线上.
(1)求圆C的方程;
(2)过点(1, )的直线截圆所得弦长为,求直线的方程.
解析
则有,解得: ,
则直线的方程为.
当直线的斜率不存在时,直线方程为,满足题意.
∴直线的方程为或.
1.判断直线与圆的位置关系有两种方法
图形
位置关系
相交
相切
相离
交点个数
2个
1个
0个
d与r关系
d
d>r
归纳小结
2.弦长问题
(1)代数法:解方程组求交点,两点间的距离公式求弦长
(2)几何法:圆心到直线的距离和勾股定理求弦长(常用)
A
B
O
(注:我们把称为弦心距.)
归纳小结
弦长公式为
P98 习题2.5:2、3、4
作 业
