高一数学 2.2.1 对数与对数运算 第一课时课件 新人教A版必修1
文档属性
| 名称 | 高一数学 2.2.1 对数与对数运算 第一课时课件 新人教A版必修1 |  | |
| 格式 | zip | ||
| 文件大小 | 306.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 08:53:03 | ||
图片预览







文档简介
课件22张PPT。§2.2 对数函数
?
2.2.1 对数与对数运算第一课时 对 数1.理解对数的概念.
2.掌握对数的基本性质. 课堂互动讲练知能优化训练第一课时 课前自主学案课前自主学案1.有理指数幂的运算性质有(1)aras=____;(2)(ab)r=____;(3)(ar)s=____.(其中a,b>0,r,s∈Q)
2.若a>0且a≠1,则当x=__时,ax=1;当x=__时,ax=a.
3.若2x=2,则x=__;若3x=9,则x=__;若2x= ,则x=____.ar+sarbrars0112-41.对数的概念
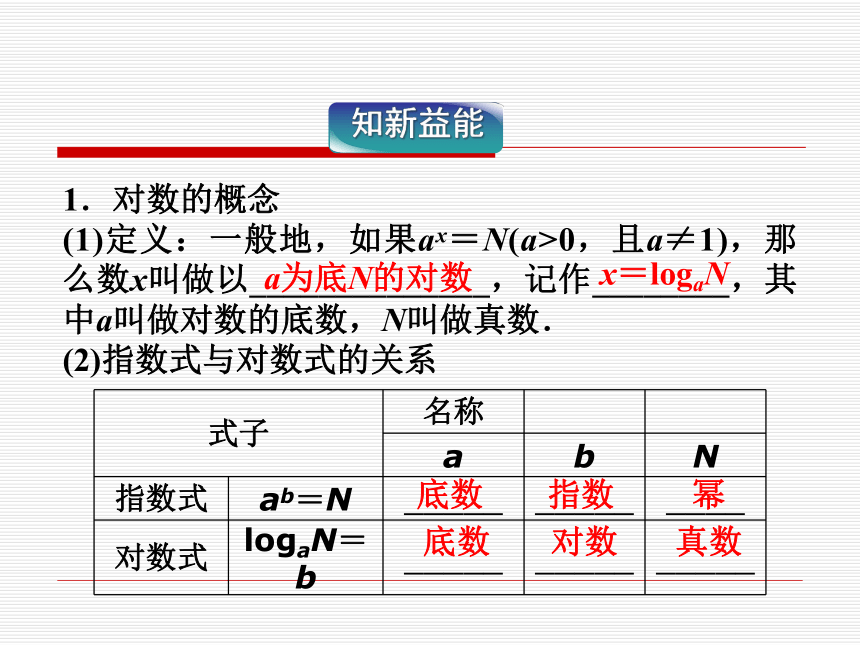
(1)定义:一般地,如果ax=N(a>0,且a≠1),那么数x叫做以______________,记作________,其中a叫做对数的底数,N叫做真数.
(2)指数式与对数式的关系a为底N的对数x=logaN底数指数幂底数对数真数2.两种特殊的对数
(1)以10为底的对数叫做________,简记为_____.
(2)以无理数e=2.71828…为底数的对数叫做__________,简记为______.
3.对数的基本性质
设a>0,且a≠1,则
(1)零和负数______对数;
(2)1的对数为零,即_________;
(3)底数的对数等于1,即_________.常用对数lgN自然对数lnN没有loga1=0logaa=11.(-3)2=9能写为log(-3)9=2吗?
提示:不可以.只有符合a>0,且a≠1且N>0时,才有ax=N?x=logaN.
2.alogaN=N(a>0,a≠1,N>0)成立吗?为什么?
提示:成立.此式称为对数恒等式.设ab=N,则b=logaN,∴ab=alogaN=N.课堂互动讲练对数式是指数式的另一种表达,求幂指数往往转化为对数;求对数值往往转化为指数幂的形式.【思路点拨】 将对数式与指数式互化,即可得解.(3)由logx25=2,得x2=25.
∵x>0,且x≠1,∴x=5.
(4)由log5x2=2,得x2=52,
∴x=±5.
∵52=25>0,(-5)2=25>0,
∴x=5或x=-5.
【名师点拨】 在指数式ab=N中,若已知a,N,求幂指数b,便是对数运算b=logaN.对数要成立必须具备底数大于0且不等于1,且真数大于0,这是对数存在的基础.
求下列各式中x的范围.
(1)log(2x-1)(x+2);(2)log (x2+1)(-3x+8).
【思路点拨】 注意到x既存在于底数中,又存在于真数中,解答本题结合对数的概念,应考虑其各自的要求解出x满足的条件.【名师点拨】 求解此类式子中参数的范围时,应根据对数中对底数和真数的要求列出不等式组解出即可.互动探究1 在本例(2)中,若底数与真数中的式子互换,即log(-3x+8)(x2+1),则x的取值范围如何?利用对数的基本性质对简单的对数式进行化简或求值.【思路点拨】 (1)(2)(3)主要利用loga1=0,logaa=1,(4)利用对数恒等式化简.
【解】 (1)∵log2(log5x)=0,
∴log5x=20=1,∴x=51=5.
(2)∵log3(lgx)=1,∴lgx=31=3,
∴x=103=1000.
【名师点拨】 有关“底数”和“1”的对数,可利用对数的性质求出其值为“1”和“0”,化成常数,有利于化简和计算.自我挑战2 若loga[logb(logcx)]=0,(a>0,b>0,c>0且a≠1,b≠1,c≠1),则x=________.
解析:logb(logcx)=1,∴logc x=b,∴x=cb.
答案:cb失误防范
1.已知含x的对数等式,确定x的值时,易忽视使其有意义的x的取值范围,也就是解对数方程不可忽视对所求x值的检验.(如例2)
2.使用对数恒等式alogaN=N化简对数式时,不要只从形式上相同就认为符合恒等式,还需使对数有意义,如(-3) log(-3)2无意义.
?
2.2.1 对数与对数运算第一课时 对 数1.理解对数的概念.
2.掌握对数的基本性质. 课堂互动讲练知能优化训练第一课时 课前自主学案课前自主学案1.有理指数幂的运算性质有(1)aras=____;(2)(ab)r=____;(3)(ar)s=____.(其中a,b>0,r,s∈Q)
2.若a>0且a≠1,则当x=__时,ax=1;当x=__时,ax=a.
3.若2x=2,则x=__;若3x=9,则x=__;若2x= ,则x=____.ar+sarbrars0112-41.对数的概念
(1)定义:一般地,如果ax=N(a>0,且a≠1),那么数x叫做以______________,记作________,其中a叫做对数的底数,N叫做真数.
(2)指数式与对数式的关系a为底N的对数x=logaN底数指数幂底数对数真数2.两种特殊的对数
(1)以10为底的对数叫做________,简记为_____.
(2)以无理数e=2.71828…为底数的对数叫做__________,简记为______.
3.对数的基本性质
设a>0,且a≠1,则
(1)零和负数______对数;
(2)1的对数为零,即_________;
(3)底数的对数等于1,即_________.常用对数lgN自然对数lnN没有loga1=0logaa=11.(-3)2=9能写为log(-3)9=2吗?
提示:不可以.只有符合a>0,且a≠1且N>0时,才有ax=N?x=logaN.
2.alogaN=N(a>0,a≠1,N>0)成立吗?为什么?
提示:成立.此式称为对数恒等式.设ab=N,则b=logaN,∴ab=alogaN=N.课堂互动讲练对数式是指数式的另一种表达,求幂指数往往转化为对数;求对数值往往转化为指数幂的形式.【思路点拨】 将对数式与指数式互化,即可得解.(3)由logx25=2,得x2=25.
∵x>0,且x≠1,∴x=5.
(4)由log5x2=2,得x2=52,
∴x=±5.
∵52=25>0,(-5)2=25>0,
∴x=5或x=-5.
【名师点拨】 在指数式ab=N中,若已知a,N,求幂指数b,便是对数运算b=logaN.对数要成立必须具备底数大于0且不等于1,且真数大于0,这是对数存在的基础.
求下列各式中x的范围.
(1)log(2x-1)(x+2);(2)log (x2+1)(-3x+8).
【思路点拨】 注意到x既存在于底数中,又存在于真数中,解答本题结合对数的概念,应考虑其各自的要求解出x满足的条件.【名师点拨】 求解此类式子中参数的范围时,应根据对数中对底数和真数的要求列出不等式组解出即可.互动探究1 在本例(2)中,若底数与真数中的式子互换,即log(-3x+8)(x2+1),则x的取值范围如何?利用对数的基本性质对简单的对数式进行化简或求值.【思路点拨】 (1)(2)(3)主要利用loga1=0,logaa=1,(4)利用对数恒等式化简.
【解】 (1)∵log2(log5x)=0,
∴log5x=20=1,∴x=51=5.
(2)∵log3(lgx)=1,∴lgx=31=3,
∴x=103=1000.
【名师点拨】 有关“底数”和“1”的对数,可利用对数的性质求出其值为“1”和“0”,化成常数,有利于化简和计算.自我挑战2 若loga[logb(logcx)]=0,(a>0,b>0,c>0且a≠1,b≠1,c≠1),则x=________.
解析:logb(logcx)=1,∴logc x=b,∴x=cb.
答案:cb失误防范
1.已知含x的对数等式,确定x的值时,易忽视使其有意义的x的取值范围,也就是解对数方程不可忽视对所求x值的检验.(如例2)
2.使用对数恒等式alogaN=N化简对数式时,不要只从形式上相同就认为符合恒等式,还需使对数有意义,如(-3) log(-3)2无意义.
