高一数学 2.3.1 幂函数的图象及性质课件 新人教A版必修1
文档属性
| 名称 | 高一数学 2.3.1 幂函数的图象及性质课件 新人教A版必修1 |

|
|
| 格式 | zip | ||
| 文件大小 | 346.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-12-13 00:00:00 | ||
图片预览






文档简介
课件19张PPT。§2.3 幂函数
?
2.3.1 幂函数的图象及性质 课堂互动讲练知能优化训练2.3.1课前自主学案课前自主学案1.一般地,形如_________________的函数叫做指数函数;形如____________________的函数叫做对数函数.
2.函数y=x-1的图象是_______,关于原点对称,定义域{x|x≠0};
函数y=x的图象是过原点的直线,关于原点对称;
函数y=x2的图象是开口向上的抛物线,关于y轴对称.y=ax(a>0,a≠1)y=logax(a>0,a≠1)双曲线1.幂函数的概念
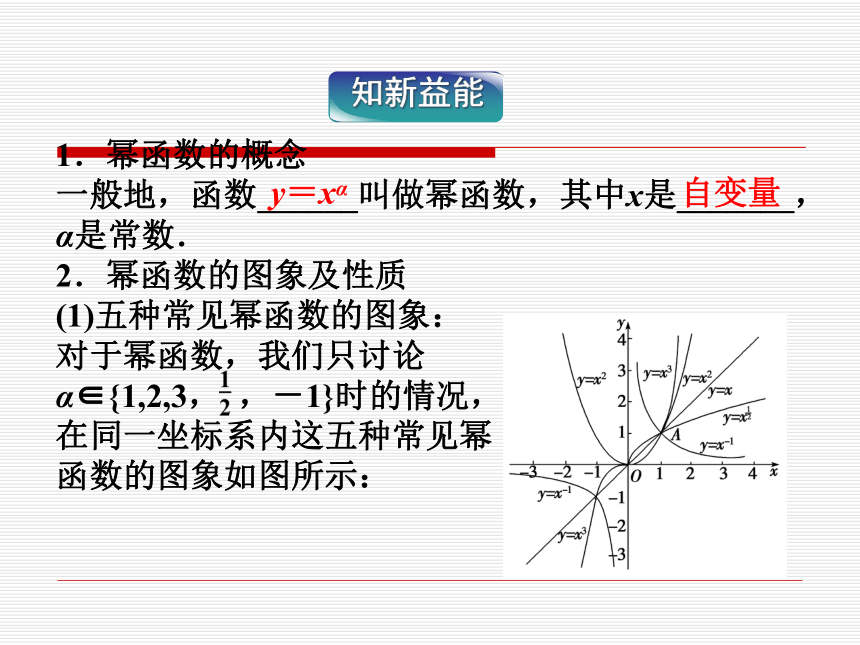
一般地,函数______叫做幂函数,其中x是_______,α是常数.
2.幂函数的图象及性质
(1)五种常见幂函数的图象:
对于幂函数,我们只讨论
α∈{1,2,3, ,-1}时的情况,
在同一坐标系内这五种常见幂
函数的图象如图所示:y=xα自变量(2)幂函数的性质1.函数y=x2与y=2x有什么区别?
提示:y=x2是幂函数,也可认为是特殊的二次函数,自变量x是幂的底数,x∈R,其图象是抛物线,而y=2x是指数函数,x是指数,其图象是单调递增的指数函数图象.
2.幂函数图象能过第四象限吗?
提示:不能.对幂函数y=xα而言,当x>0时,必有y>0,故幂函数图象不过第四象限.课堂互动讲练主要考查幂函数的解析式的特征. 若函数y=(m2-m-1)x-5m-3为幂函数,则m=________.
【思路点拨】 只要使m2-m-1=1,就成为幂函数.【解析】 令m2-m-1=1,
∴m=2或m=-1.
当m=2时,函数y=x-13,
当m=-1时,函数y=x2,都是幂函数.
【答案】 2或-1
【名师点拨】 y=xα其特征底数为自变量x,指数α为常数,且系数为1.互动探究1 在本例中,若当x∈(0,+∞)时,y=(m2-m-1)x-5m-3为减函数,m取何值?根据幂函数图象的特征,待定解析式,利用图象解决问题.【思路点拨】 用待定系数法求解析式;结合图形解决x的取值问题.(2)在同一坐标系下作出f(x)=x2和g(x)=x-2的图象如图所示.由图象可知:
①当x>1或x<-1时,
f(x)>g(x);
②当x=1或x=-1时,f(x)=g(x);
③当-1【名师点拨】 (1)求幂函数解析式的步骤:①设出幂函数的一般形式y=xα(α为常数);②根据已知条件求出α的值;③写出幂函数的解析式.解:(1)g(x)=x-1.
(2)分别作出它们的图象如图所示,
由图象可知,当x∈(-∞,0)∪(1,+∞)时,f(x)>g(x);
当x=1时,f(x)=g(x);
当x∈(0,1)时,f(x)1.利用幂函数的定义,抓住其本质特征,这是判断一个函数是否为幂函数的重要依据和唯一标准.(如例1)
2.对于幂函数y=xa的图象,在直线x=1的右侧,若图象越高,则a的值就越大.如例2.
3.利用幂函数图象解题时,要抓住幂函数图象的交叉点(分界点)在第一象限为(1,1),在第二象限为(-1,1),第三象限为(-1,-1).失误防范
1.注意区分幂函数y=xα与指数函数y=ax的区别,二者极易混淆.
2.注意区分幂函数与正比例函数、反比例函数、二次函数的区别.
?
2.3.1 幂函数的图象及性质 课堂互动讲练知能优化训练2.3.1课前自主学案课前自主学案1.一般地,形如_________________的函数叫做指数函数;形如____________________的函数叫做对数函数.
2.函数y=x-1的图象是_______,关于原点对称,定义域{x|x≠0};
函数y=x的图象是过原点的直线,关于原点对称;
函数y=x2的图象是开口向上的抛物线,关于y轴对称.y=ax(a>0,a≠1)y=logax(a>0,a≠1)双曲线1.幂函数的概念
一般地,函数______叫做幂函数,其中x是_______,α是常数.
2.幂函数的图象及性质
(1)五种常见幂函数的图象:
对于幂函数,我们只讨论
α∈{1,2,3, ,-1}时的情况,
在同一坐标系内这五种常见幂
函数的图象如图所示:y=xα自变量(2)幂函数的性质1.函数y=x2与y=2x有什么区别?
提示:y=x2是幂函数,也可认为是特殊的二次函数,自变量x是幂的底数,x∈R,其图象是抛物线,而y=2x是指数函数,x是指数,其图象是单调递增的指数函数图象.
2.幂函数图象能过第四象限吗?
提示:不能.对幂函数y=xα而言,当x>0时,必有y>0,故幂函数图象不过第四象限.课堂互动讲练主要考查幂函数的解析式的特征. 若函数y=(m2-m-1)x-5m-3为幂函数,则m=________.
【思路点拨】 只要使m2-m-1=1,就成为幂函数.【解析】 令m2-m-1=1,
∴m=2或m=-1.
当m=2时,函数y=x-13,
当m=-1时,函数y=x2,都是幂函数.
【答案】 2或-1
【名师点拨】 y=xα其特征底数为自变量x,指数α为常数,且系数为1.互动探究1 在本例中,若当x∈(0,+∞)时,y=(m2-m-1)x-5m-3为减函数,m取何值?根据幂函数图象的特征,待定解析式,利用图象解决问题.【思路点拨】 用待定系数法求解析式;结合图形解决x的取值问题.(2)在同一坐标系下作出f(x)=x2和g(x)=x-2的图象如图所示.由图象可知:
①当x>1或x<-1时,
f(x)>g(x);
②当x=1或x=-1时,f(x)=g(x);
③当-1
(2)分别作出它们的图象如图所示,
由图象可知,当x∈(-∞,0)∪(1,+∞)时,f(x)>g(x);
当x=1时,f(x)=g(x);
当x∈(0,1)时,f(x)
2.对于幂函数y=xa的图象,在直线x=1的右侧,若图象越高,则a的值就越大.如例2.
3.利用幂函数图象解题时,要抓住幂函数图象的交叉点(分界点)在第一象限为(1,1),在第二象限为(-1,1),第三象限为(-1,-1).失误防范
1.注意区分幂函数y=xα与指数函数y=ax的区别,二者极易混淆.
2.注意区分幂函数与正比例函数、反比例函数、二次函数的区别.
