人教A版(2019)高中数学选择性必修第一册 3.1.2《椭圆的简单几何性质---第二课时》名师课件(共37张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学选择性必修第一册 3.1.2《椭圆的简单几何性质---第二课时》名师课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 16:25:32 | ||
图片预览










文档简介
(共37张PPT)
椭圆的简单几何性质
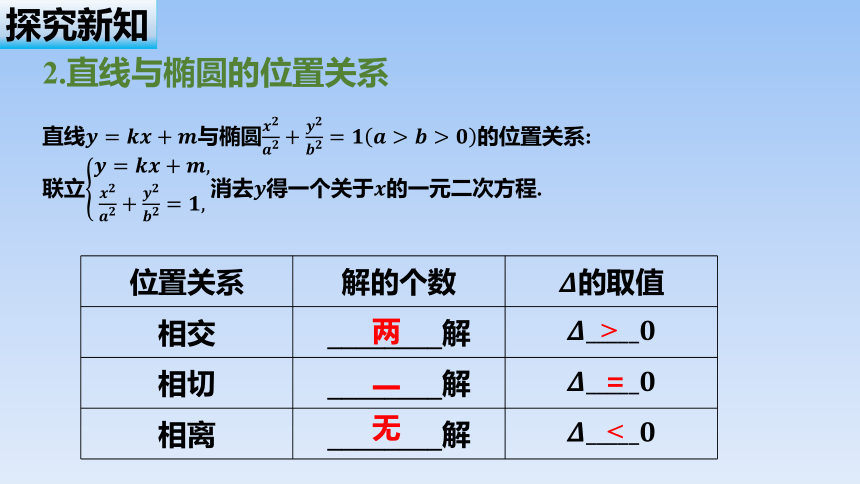
焦点的位置 焦点在轴上 焦点在轴上
图形
复习引入
标准方程 ___________________
___________________
范围 _____________ ____________ ____________
___________
顶点 __________________ ___________________ ___________________
_________________
轴长 短轴长= ,长轴长=___
复习引入
椭圆的简单几何性质
焦点
焦距 =_________
对称性 对称轴: 对称中心:_____
离心率 e= ∈_____
轴、轴
原点
复习引入
椭圆的简单几何性质
人教A版同步教材名师课件
椭圆的简单几何性质
---第二课时
探究新知
大家知道,直线与圆有三种位置关系,设圆心到直线的距离为,圆的半径为,则
时 直线与圆相离;
时 直线与圆相切;
时 直线与圆相交.
那么直线与椭圆有几种位置关系呢 又如何来判定呢
探究新知
1.点与椭圆的位置关系
点与椭圆的位置关系:
点在椭圆上______________;
点在椭圆内部____________;
点在椭圆外部____________.
探究新知
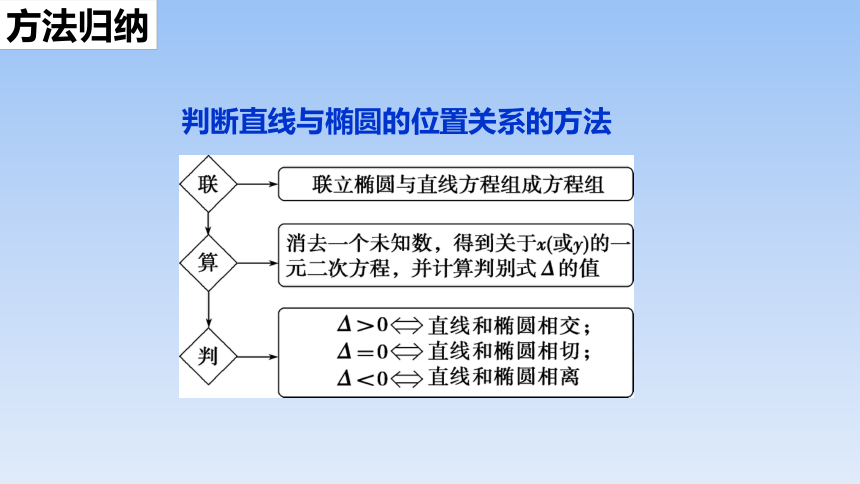
2.直线与椭圆的位置关系
直线与椭圆的位置关系:
联立消去得一个关于的一元二次方程.
位置关系 解的个数 的取值
相交 ________解
相切 ________解
相离 ________解
两
>
一
=
无
<
探究新知
根据椭圆的对称性知,两交点关于原点对称.
提示
思考:
过原点的直线和椭圆相交,两交点关于原点对称吗
典例讲解
直线的方程与椭圆的方程联立,得方程组
消去,得.①
例1、已知直线,椭圆.试问当取何值时,直线与椭圆:
(1)有两个公共点;(2)有且只有一个公共点;(3)没有公共点.
解析
方程①的判别式
(1)当,即时,方程①有两个不同的实数解,可知原方程组有两组不同的实数解.这时直线与椭圆有两个不同的公共点.
典例讲解
解析
(2)当,即时,方程①有两个相同的实数解,
可知原方程组有两组相同的实数解.
这时直线与椭圆有且只有一个公共点.
(3)当,即或时,方程①没有实数解,
可知原方程组没有实数解.
这时直线与椭圆没有公共点.
例1、已知直线,椭圆.试问当取何值时,直线与椭圆:
(1)有两个公共点;(2)有且只有一个公共点;(3)没有公共点.
判断直线与椭圆的位置关系的方法
方法归纳
变式训练
1.(1)直线与椭圆的位置关系为________. (填相交、相切或相离).
(2)若直线与椭圆有两个不同的公共点,则实数的取值范围是_____________.
相离
(1)由得即
因此直线与椭圆没有公共点.
解析
变式训练
(2)由可得,
当,
即或时,直线与椭圆有两个不同的公共点.
1.(1)直线与椭圆的位置关系为________. (填相交、相切或相离).
(2)若直线与椭圆有两个不同的公共点,则实数的取值范围是_____________.
相离
解析
典例讲解
(1)由已知可得直线的方程为,即.
由可得
若设
则, .
例2、已知椭圆和点,直线经过点且与椭圆交于两点.
(1)当直线的斜率为时,求线段的长度;
(2)当点恰好为线段的中点时,求的方程.
解析
典例讲解
于是
所以线段的长度为
例2、已知椭圆和点,直线经过点且与椭圆交于两点.
(1)当直线的斜率为时,求线段的长度;
(2)当点恰好为线段的中点时,求的方程.
解析
典例讲解
(2)法一:易知的斜率存在,不妨设为,则其方程为.
联立
消去得
若设
则, 由于的中点恰好为,
所以,解得 ,且满足.
这时直线的方程为即
例2、已知椭圆和点,直线经过点且与椭圆交于两点.
(2)当点恰好为线段的中点时,求的方程.
解析
典例讲解
法二:设, ,则有
两式相减得
整理得,
由于是的中点,所以, ,
于是,于是直线的方程为
即
例2、已知椭圆和点,直线经过点且与椭圆交于两点.
(2)当点恰好为线段的中点时,求的方程.
解析
①求弦长的方法:将直线方程与椭圆方程联立,得到关于x的一元二次方程,然后运用根与系数的关系,再求弦长.不必具体求出方程的根,即不必求出直线与椭圆的交点.这种方法是求弦长常采用的方法.
(1)直线与椭圆相交弦的弦长问题
当直线与椭圆相交时,两交点间的距离,称为弦长.
②求弦长的公式:设直线l的斜率为,方程为,设端点, .
方法归纳
(为直线斜率).
①根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用一元二次方程根与系数的关系以及中点坐标公式解决.
(2)解决椭圆中点弦问题的两种方法
方法归纳
②点差法:利用交点在曲线上,坐标满足方程,将交点坐标分别代入椭圆方程,然后作差,构造出中点坐标和斜率的关系,具体如下:已知,是
上的两个不同的点,是线段的中点,
则由,得 ,
变形得,
即
变式训练
因为,所以.所以椭圆方程为.
与联立消去,得,
由得,
由弦长公式得
所以
所以椭圆方程为.
2.椭圆的离心率为,且椭圆与直线相交于,且,求椭圆方程.
解析
典例讲解
例、椭圆经过点,且离心率为.
(1)求椭圆的方程;
(2)过点任作一条直线与椭圆交于不同的两点.在轴上是否存在点,使得 若存在,求出点的坐标;若不存在,请说明理由.
(1)由条件可知,椭圆的焦点在轴上,且,又
得.
由得所求椭圆的方程为.
解析
典例讲解
(2)若存在点,使得,则直线和的斜率存在,
分别设为,等价于.
依题意,直线的斜率存在,故设直线的方程为.
由
得.
因为直线与椭圆有两个交点,所以.
即,解得.
例、椭圆经过点,且离心率为.
(2)过点任作一条直线与椭圆交于不同的两点.在轴上是否存在点,使得 若存在,求出点的坐标;若不存在,请说明理由.
解析
典例讲解
设,,则, ,
,
令
当时, ,
化简得, 所以.
当时,也成立.所以存在点,使得
例、椭圆经过点,且离心率为.
(2)过点任作一条直线与椭圆交于不同的两点.在轴上是否存在点,使得 若存在,求出点的坐标;若不存在,请说明理由.
解析
方法归纳
综合问题涉及的问题及解决方法
本题主要考查了直线与椭圆的位置关系的综合问题,
其中解答中涉及到椭圆的几何性质及其应用,直线与椭圆的位置关系的综合应用,
着重考查了学生分析问题和解答问题的能力,推理与运算能力.
此类问题的解答中,把直线方程代入椭圆的方程,转化为方程的根与系数的关系是解答的关键.
变式训练
3.椭圆的两个焦点坐标分别 为和,且椭圆过点
(1)求椭圆方程;
(2)过点作不与轴垂直的直线交该椭圆于两点,为椭圆的左顶点,试判断的大小是否为定值,并说明理由.
(1)由题意设椭圆方程,
由, ,代入方程
又∵椭圆过点,
得,解得,所以.
椭圆的方程为.
解析
变式训练
(2)设直线的方程为
联立直线和椭圆的方程可得
得
设
3.椭圆的两个焦点坐标分别 为和,且椭圆过点
(1)求椭圆方程;
(2)过点作不与轴垂直的直线交该椭圆于两点,为椭圆的左顶点,试判断的大小是否为定值,并说明理由.
解析
变式训练
,
则
,
即可得.
∴ 的大小是定值.
3.椭圆的两个焦点坐标分别 为和,且椭圆过点
(1)求椭圆方程;
(2)过点作不与轴垂直的直线交该椭圆于两点,为椭圆的左顶点,试判断的大小是否为定值,并说明理由.
解析
(1)设直线与椭圆的交点为;
(2)联立直线与椭圆的方程;
(3)消元得到关于或的一元二次方程;
(4)利用根与系数的关系设而不求;
(5)把题干中的条件转化为或进而求解.
1.解决直线与椭圆的位置关系问题经常利用设而不求的方法.
解题步骤为:
素养提炼
素养提炼
过椭圆的焦点且垂直于长轴的直线被椭圆截得的弦称为椭圆的通径,
其长度的求法如下:
在椭圆中,令,得,
则,所以,
所以通径长为.
2.椭圆的通径
当堂练习
1.若点在椭圆的外部,则的取值范围为( )
A. B.
由题意知,即,解得或.
B
解析
当堂练习
2.已知椭圆的左、右顶点分别为,且以线段为直径的圆与直线相切,则的离心率为( )
由题意知以为直径的圆的圆心为半径为.
又直线与圆相切,
∴圆心到直线的距离,解得
∴
∴
故选.
解析
当堂练习
3.设椭圆的左、右焦点分别为,,过焦点的直线交椭圆于两点,若的内切圆的面积为,则.
如图,已知椭圆的左、右焦点分别为,,
,过焦点的直线交椭圆于两点, 的内切圆的面积为,
∴ 的内切圆半径.
∴的面积
解析
当堂练习
由
消去并化简得.
设直线与椭圆的交点为,
则, .
∴弦长
4.椭圆.被直线截得的弦长为___________.
解析
当堂练习
5.设椭圆过点,离心率为.
(1)求椭圆的方程;
(2)求过点且斜率为的直线被所截线段的中点的坐标.
(1)将代入的方程,得
.
由,得
即, ,
椭圆C的方程为
解析
当堂练习
(2)过点且斜率为的直线方程为.
设直线与C的交点为,,
将直线的方程代入C的方程,得,
即,
则,∴
即中点的坐标为.
解析
5.设椭圆过点,离心率为.
(2)求过点且斜率为的直线被所截线段的中点的坐标.
判断直线与椭圆的位置关系的方法
归纳小结
P115:9、13、14
作 业
椭圆的简单几何性质
焦点的位置 焦点在轴上 焦点在轴上
图形
复习引入
标准方程 ___________________
___________________
范围 _____________ ____________ ____________
___________
顶点 __________________ ___________________ ___________________
_________________
轴长 短轴长= ,长轴长=___
复习引入
椭圆的简单几何性质
焦点
焦距 =_________
对称性 对称轴: 对称中心:_____
离心率 e= ∈_____
轴、轴
原点
复习引入
椭圆的简单几何性质
人教A版同步教材名师课件
椭圆的简单几何性质
---第二课时
探究新知
大家知道,直线与圆有三种位置关系,设圆心到直线的距离为,圆的半径为,则
时 直线与圆相离;
时 直线与圆相切;
时 直线与圆相交.
那么直线与椭圆有几种位置关系呢 又如何来判定呢
探究新知
1.点与椭圆的位置关系
点与椭圆的位置关系:
点在椭圆上______________;
点在椭圆内部____________;
点在椭圆外部____________.
探究新知
2.直线与椭圆的位置关系
直线与椭圆的位置关系:
联立消去得一个关于的一元二次方程.
位置关系 解的个数 的取值
相交 ________解
相切 ________解
相离 ________解
两
>
一
=
无
<
探究新知
根据椭圆的对称性知,两交点关于原点对称.
提示
思考:
过原点的直线和椭圆相交,两交点关于原点对称吗
典例讲解
直线的方程与椭圆的方程联立,得方程组
消去,得.①
例1、已知直线,椭圆.试问当取何值时,直线与椭圆:
(1)有两个公共点;(2)有且只有一个公共点;(3)没有公共点.
解析
方程①的判别式
(1)当,即时,方程①有两个不同的实数解,可知原方程组有两组不同的实数解.这时直线与椭圆有两个不同的公共点.
典例讲解
解析
(2)当,即时,方程①有两个相同的实数解,
可知原方程组有两组相同的实数解.
这时直线与椭圆有且只有一个公共点.
(3)当,即或时,方程①没有实数解,
可知原方程组没有实数解.
这时直线与椭圆没有公共点.
例1、已知直线,椭圆.试问当取何值时,直线与椭圆:
(1)有两个公共点;(2)有且只有一个公共点;(3)没有公共点.
判断直线与椭圆的位置关系的方法
方法归纳
变式训练
1.(1)直线与椭圆的位置关系为________. (填相交、相切或相离).
(2)若直线与椭圆有两个不同的公共点,则实数的取值范围是_____________.
相离
(1)由得即
因此直线与椭圆没有公共点.
解析
变式训练
(2)由可得,
当,
即或时,直线与椭圆有两个不同的公共点.
1.(1)直线与椭圆的位置关系为________. (填相交、相切或相离).
(2)若直线与椭圆有两个不同的公共点,则实数的取值范围是_____________.
相离
解析
典例讲解
(1)由已知可得直线的方程为,即.
由可得
若设
则, .
例2、已知椭圆和点,直线经过点且与椭圆交于两点.
(1)当直线的斜率为时,求线段的长度;
(2)当点恰好为线段的中点时,求的方程.
解析
典例讲解
于是
所以线段的长度为
例2、已知椭圆和点,直线经过点且与椭圆交于两点.
(1)当直线的斜率为时,求线段的长度;
(2)当点恰好为线段的中点时,求的方程.
解析
典例讲解
(2)法一:易知的斜率存在,不妨设为,则其方程为.
联立
消去得
若设
则, 由于的中点恰好为,
所以,解得 ,且满足.
这时直线的方程为即
例2、已知椭圆和点,直线经过点且与椭圆交于两点.
(2)当点恰好为线段的中点时,求的方程.
解析
典例讲解
法二:设, ,则有
两式相减得
整理得,
由于是的中点,所以, ,
于是,于是直线的方程为
即
例2、已知椭圆和点,直线经过点且与椭圆交于两点.
(2)当点恰好为线段的中点时,求的方程.
解析
①求弦长的方法:将直线方程与椭圆方程联立,得到关于x的一元二次方程,然后运用根与系数的关系,再求弦长.不必具体求出方程的根,即不必求出直线与椭圆的交点.这种方法是求弦长常采用的方法.
(1)直线与椭圆相交弦的弦长问题
当直线与椭圆相交时,两交点间的距离,称为弦长.
②求弦长的公式:设直线l的斜率为,方程为,设端点, .
方法归纳
(为直线斜率).
①根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用一元二次方程根与系数的关系以及中点坐标公式解决.
(2)解决椭圆中点弦问题的两种方法
方法归纳
②点差法:利用交点在曲线上,坐标满足方程,将交点坐标分别代入椭圆方程,然后作差,构造出中点坐标和斜率的关系,具体如下:已知,是
上的两个不同的点,是线段的中点,
则由,得 ,
变形得,
即
变式训练
因为,所以.所以椭圆方程为.
与联立消去,得,
由得,
由弦长公式得
所以
所以椭圆方程为.
2.椭圆的离心率为,且椭圆与直线相交于,且,求椭圆方程.
解析
典例讲解
例、椭圆经过点,且离心率为.
(1)求椭圆的方程;
(2)过点任作一条直线与椭圆交于不同的两点.在轴上是否存在点,使得 若存在,求出点的坐标;若不存在,请说明理由.
(1)由条件可知,椭圆的焦点在轴上,且,又
得.
由得所求椭圆的方程为.
解析
典例讲解
(2)若存在点,使得,则直线和的斜率存在,
分别设为,等价于.
依题意,直线的斜率存在,故设直线的方程为.
由
得.
因为直线与椭圆有两个交点,所以.
即,解得.
例、椭圆经过点,且离心率为.
(2)过点任作一条直线与椭圆交于不同的两点.在轴上是否存在点,使得 若存在,求出点的坐标;若不存在,请说明理由.
解析
典例讲解
设,,则, ,
,
令
当时, ,
化简得, 所以.
当时,也成立.所以存在点,使得
例、椭圆经过点,且离心率为.
(2)过点任作一条直线与椭圆交于不同的两点.在轴上是否存在点,使得 若存在,求出点的坐标;若不存在,请说明理由.
解析
方法归纳
综合问题涉及的问题及解决方法
本题主要考查了直线与椭圆的位置关系的综合问题,
其中解答中涉及到椭圆的几何性质及其应用,直线与椭圆的位置关系的综合应用,
着重考查了学生分析问题和解答问题的能力,推理与运算能力.
此类问题的解答中,把直线方程代入椭圆的方程,转化为方程的根与系数的关系是解答的关键.
变式训练
3.椭圆的两个焦点坐标分别 为和,且椭圆过点
(1)求椭圆方程;
(2)过点作不与轴垂直的直线交该椭圆于两点,为椭圆的左顶点,试判断的大小是否为定值,并说明理由.
(1)由题意设椭圆方程,
由, ,代入方程
又∵椭圆过点,
得,解得,所以.
椭圆的方程为.
解析
变式训练
(2)设直线的方程为
联立直线和椭圆的方程可得
得
设
3.椭圆的两个焦点坐标分别 为和,且椭圆过点
(1)求椭圆方程;
(2)过点作不与轴垂直的直线交该椭圆于两点,为椭圆的左顶点,试判断的大小是否为定值,并说明理由.
解析
变式训练
,
则
,
即可得.
∴ 的大小是定值.
3.椭圆的两个焦点坐标分别 为和,且椭圆过点
(1)求椭圆方程;
(2)过点作不与轴垂直的直线交该椭圆于两点,为椭圆的左顶点,试判断的大小是否为定值,并说明理由.
解析
(1)设直线与椭圆的交点为;
(2)联立直线与椭圆的方程;
(3)消元得到关于或的一元二次方程;
(4)利用根与系数的关系设而不求;
(5)把题干中的条件转化为或进而求解.
1.解决直线与椭圆的位置关系问题经常利用设而不求的方法.
解题步骤为:
素养提炼
素养提炼
过椭圆的焦点且垂直于长轴的直线被椭圆截得的弦称为椭圆的通径,
其长度的求法如下:
在椭圆中,令,得,
则,所以,
所以通径长为.
2.椭圆的通径
当堂练习
1.若点在椭圆的外部,则的取值范围为( )
A. B.
由题意知,即,解得或.
B
解析
当堂练习
2.已知椭圆的左、右顶点分别为,且以线段为直径的圆与直线相切,则的离心率为( )
由题意知以为直径的圆的圆心为半径为.
又直线与圆相切,
∴圆心到直线的距离,解得
∴
∴
故选.
解析
当堂练习
3.设椭圆的左、右焦点分别为,,过焦点的直线交椭圆于两点,若的内切圆的面积为,则.
如图,已知椭圆的左、右焦点分别为,,
,过焦点的直线交椭圆于两点, 的内切圆的面积为,
∴ 的内切圆半径.
∴的面积
解析
当堂练习
由
消去并化简得.
设直线与椭圆的交点为,
则, .
∴弦长
4.椭圆.被直线截得的弦长为___________.
解析
当堂练习
5.设椭圆过点,离心率为.
(1)求椭圆的方程;
(2)求过点且斜率为的直线被所截线段的中点的坐标.
(1)将代入的方程,得
.
由,得
即, ,
椭圆C的方程为
解析
当堂练习
(2)过点且斜率为的直线方程为.
设直线与C的交点为,,
将直线的方程代入C的方程,得,
即,
则,∴
即中点的坐标为.
解析
5.设椭圆过点,离心率为.
(2)求过点且斜率为的直线被所截线段的中点的坐标.
判断直线与椭圆的位置关系的方法
归纳小结
P115:9、13、14
作 业
