人教版九年级数学上册24.2.1点和圆的位置关系 (第1-2课时) 导学案+作业设计(含答案)
文档属性
| 名称 | 人教版九年级数学上册24.2.1点和圆的位置关系 (第1-2课时) 导学案+作业设计(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-20 18:14:24 | ||
图片预览


文档简介
人教版九年级数学上册第二十四章
《点和圆的位置关系》学习任务单及作业设计
第一课时
【学习目标】
1.了解点和圆的位置关系关注数形之间的转化,
2.过一点、过两点可以作无数个圆,并熟知圆心分布.
【课前学习任务】
回顾本章知识结构图,认清本节课所处的位置.
【课上学习任务】
学习任务一:整理概念:点和圆的位置关系
设⊙O 的半径为 r,点P到圆心的距离为d,则有
点P在圆外,则 d>r ;
点P在圆上,则d=r ;
点P在圆内,则d<r .
学习任务二:巩固练习
1.画出由所有到已知点O的距离大于或
等于2cm,并且小于或等于3cm 的点组成的图形.
(请用刻度尺和圆规)
2.体育课上,小明和小丽的铅球成绩分别是
6.4 m 和 5.1 m ,他们投出的铅球分别落在图中哪个区域内?
小明的铅球落在6分到7分的区域,小丽的铅球落在5分到6分的区域。
3.已知⊙O 的面积为 25π:
(1)若 PO=5.5,则点 P 在 ;
(2)若 PO=4,则点 P 在 ;
(3)若 PO= ,则点 P 在圆上;
(4)若点 P 不在圆外,则 PO_________。
(答案:圆外,圆内,5,≤5.)
学习任务三:
探究“过已知点作圆”
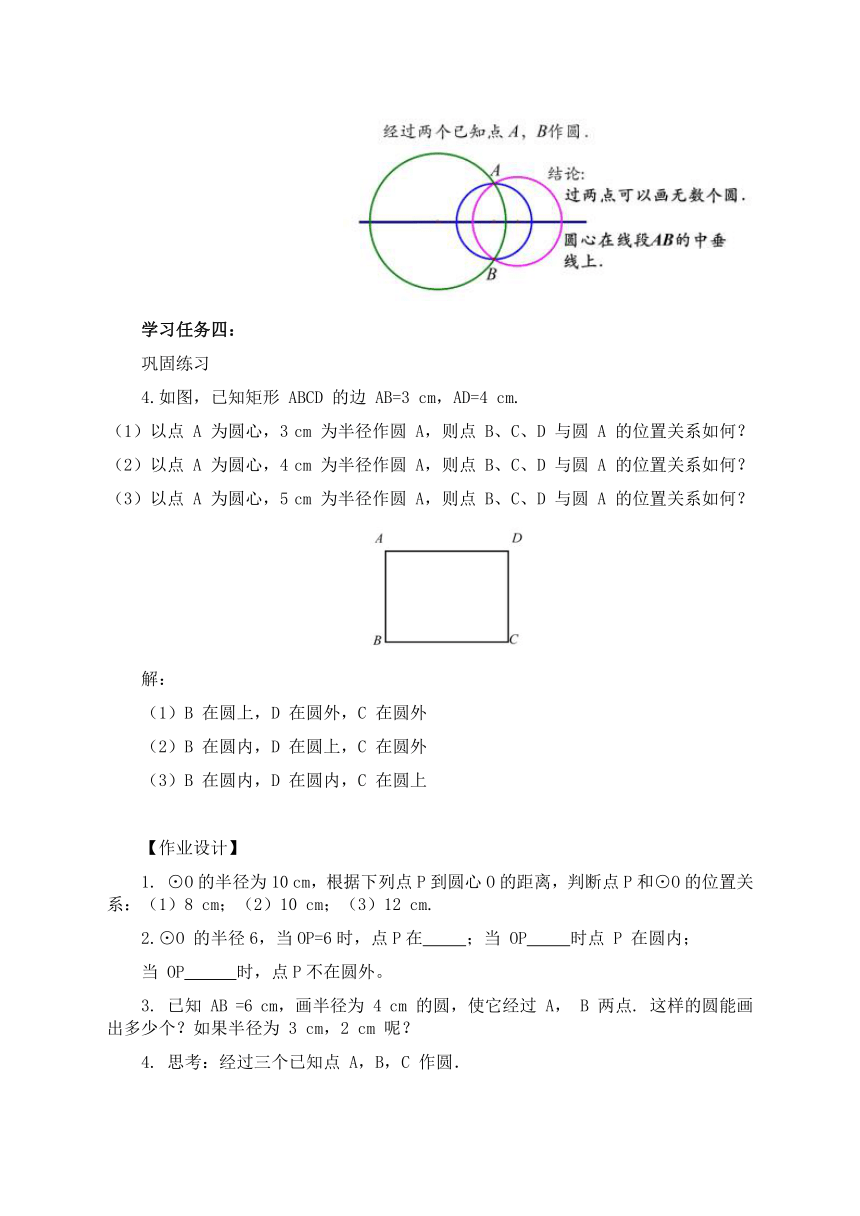
1.经过一个已知点 A 作圆.↓ 2.经过两个已知点 A,B 作圆.↓
学习任务四:
巩固练习
4.如图,已知矩形 ABCD 的边 AB=3 cm,AD=4 cm.
(1)以点 A 为圆心,3 cm 为半径作圆 A,则点 B、C、D 与圆 A 的位置关系如何?
(2)以点 A 为圆心,4 cm 为半径作圆 A,则点 B、C、D 与圆 A 的位置关系如何?
(3)以点 A 为圆心,5 cm 为半径作圆 A,则点 B、C、D 与圆 A 的位置关系如何?
解:
(1)B 在圆上,D 在圆外,C 在圆外
(2)B 在圆内,D 在圆上,C 在圆外
(3)B 在圆内,D 在圆内,C 在圆上
【作业设计】
1. ⊙O的半径为10 cm,根据下列点P到圆心O的距离,判断点P和⊙O的位置关系:(1)8 cm;(2)10 cm;(3)12 cm.
2.⊙O 的半径6,当OP=6时,点P在 ;当 OP 时点 P 在圆内;
当 OP 时,点P不在圆外。
3. 已知 AB =6 cm,画半径为 4 cm 的圆,使它经过 A, B 两点. 这样的圆能画出多少个?如果半径为 3 cm,2 cm 呢?
4. 思考:经过三个已知点 A,B,C 作圆.
【参考答案】
1. 答:(1)点 P 在⊙O 的内; (2)点 P 在⊙O 的上;(3)点 P 在⊙O 的外.
2. 答:圆上;<6;≤6.
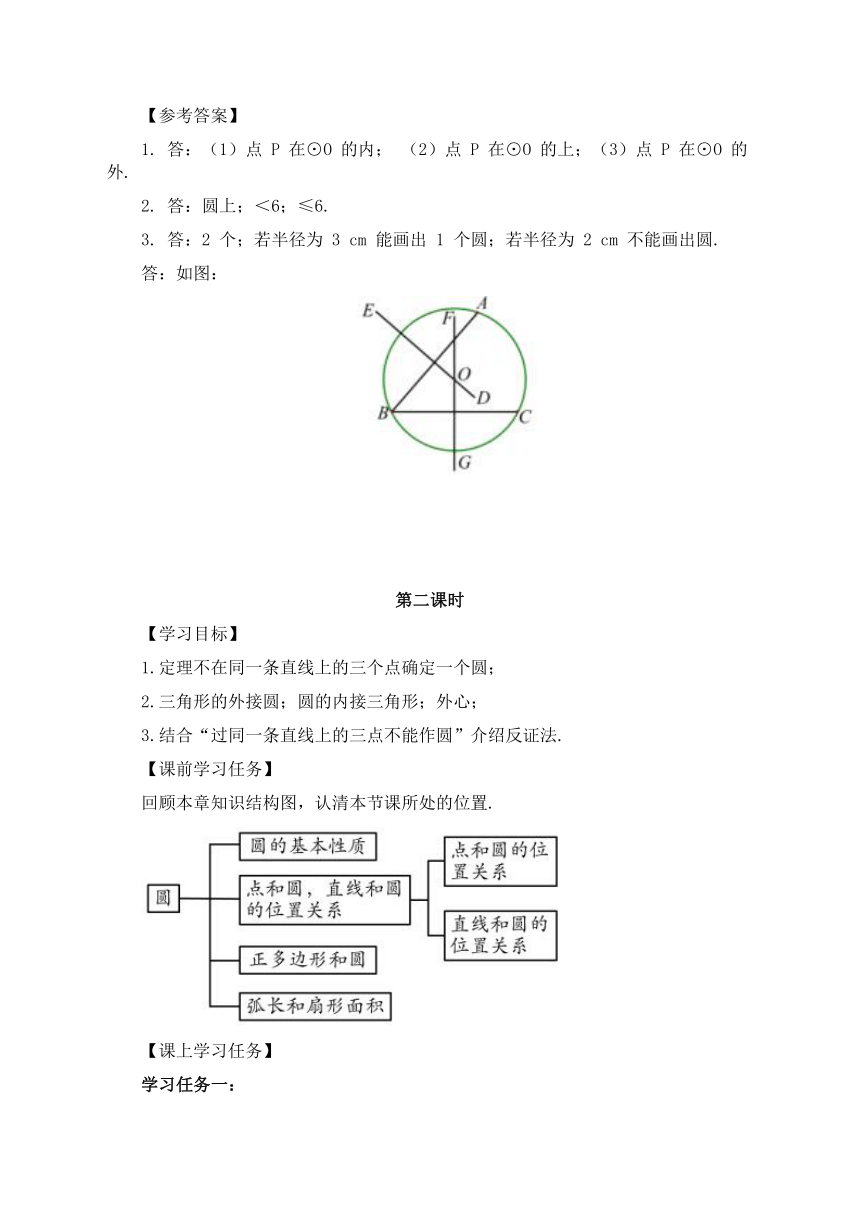
3. 答:2 个;若半径为 3 cm 能画出 1 个圆;若半径为 2 cm 不能画出圆.
答:如图:
第二课时
【学习目标】
1.定理不在同一条直线上的三个点确定一个圆;
2.三角形的外接圆;圆的内接三角形;外心;
3.结合“过同一条直线上的三点不能作圆”介绍反证法.
【课前学习任务】
回顾本章知识结构图,认清本节课所处的位置.
【课上学习任务】
学习任务一:
请同学们画三个点 A,B,C.
答案:两种情况,如下图
学习任务二:
经过不在同一条直线上的三个点 A,B,C 能不能作圆?如果能,如何确定所作圆的圆心?
结论:不在同一条直线上的三个点确定一个圆.
学习任务三:补全概念
学习任务四:
请作出锐角三角形、 直角三角形、 钝角三角形的外接圆. 这些外接圆的圆心在什么位置?
答:锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
学习任务五:
巩固练习
2.小腾家的圆形镜子损坏了,他要定制一个大小相同的新镜子,如何测量镜子的半径?
3.如图,已知 Rt△ABC 中,若∠C=90°,AC=5 cm,BC=12 cm,求△ABC 的外接圆半径.
学习任务六:
假设 命题的结论 不成立, 经过推理得出 矛盾 , 由 矛盾 判定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
学习任务七:
巩固练习
4.判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
答案:√,×,×,√.
5.若一个三角形的外心在一边上,则此三角形的形状为( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等边三角形
答案:B.
【作业设计】
1.如图,分别作出锐角三角形、直角三角形和钝角三角形的外接圆,它们外心的位置有什么特点?
2.如图是一名考古学家发现的一块古代车轮的碎片,你能帮他找出这个轮子的半?说出你的理由.
试一试:
请用反证法证明“两直线平行,同位角相等”.
已知:AB∥CD,求证:∠1=∠2.
思考:
经过任意四个点是不是可以作一个圆?
【参考答案】
1.答案:锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
2. 答案:
试一试:
证明:先假设∠1≠∠2,
过点 O 作直线 A’B’,使∠EOB’=∠2.
∴A’B’∥CD (同位角相等,两直线平行)
这样,过点 O 就有两条直线 AB、A’B’都平行 CD,
这与平行公理“过直线外一点有且仅有一条直线与已知直线平行”矛盾.
∴假设∠1≠∠2 不正确,
∴∠1=∠2.
思考:
答:根据我们今天学习的经验,我们应该首先对这四个点的位置关系进行分类,从四点在同一条直线上,四个点中有三个点在同一条直线上另一点不在,四点中任意三点都不在同一条直线上去思考.
四点在同一条直线上,不能作圆;
四点中有三个点在同一条直线上另一点不在,不能作圆;
四点中任意三点都不在同一条直线上,有可能作一个圆,也有可能做不出一个圆.
《点和圆的位置关系》学习任务单及作业设计
第一课时
【学习目标】
1.了解点和圆的位置关系关注数形之间的转化,
2.过一点、过两点可以作无数个圆,并熟知圆心分布.
【课前学习任务】
回顾本章知识结构图,认清本节课所处的位置.
【课上学习任务】
学习任务一:整理概念:点和圆的位置关系
设⊙O 的半径为 r,点P到圆心的距离为d,则有
点P在圆外,则 d>r ;
点P在圆上,则d=r ;
点P在圆内,则d<r .
学习任务二:巩固练习
1.画出由所有到已知点O的距离大于或
等于2cm,并且小于或等于3cm 的点组成的图形.
(请用刻度尺和圆规)
2.体育课上,小明和小丽的铅球成绩分别是
6.4 m 和 5.1 m ,他们投出的铅球分别落在图中哪个区域内?
小明的铅球落在6分到7分的区域,小丽的铅球落在5分到6分的区域。
3.已知⊙O 的面积为 25π:
(1)若 PO=5.5,则点 P 在 ;
(2)若 PO=4,则点 P 在 ;
(3)若 PO= ,则点 P 在圆上;
(4)若点 P 不在圆外,则 PO_________。
(答案:圆外,圆内,5,≤5.)
学习任务三:
探究“过已知点作圆”
1.经过一个已知点 A 作圆.↓ 2.经过两个已知点 A,B 作圆.↓
学习任务四:
巩固练习
4.如图,已知矩形 ABCD 的边 AB=3 cm,AD=4 cm.
(1)以点 A 为圆心,3 cm 为半径作圆 A,则点 B、C、D 与圆 A 的位置关系如何?
(2)以点 A 为圆心,4 cm 为半径作圆 A,则点 B、C、D 与圆 A 的位置关系如何?
(3)以点 A 为圆心,5 cm 为半径作圆 A,则点 B、C、D 与圆 A 的位置关系如何?
解:
(1)B 在圆上,D 在圆外,C 在圆外
(2)B 在圆内,D 在圆上,C 在圆外
(3)B 在圆内,D 在圆内,C 在圆上
【作业设计】
1. ⊙O的半径为10 cm,根据下列点P到圆心O的距离,判断点P和⊙O的位置关系:(1)8 cm;(2)10 cm;(3)12 cm.
2.⊙O 的半径6,当OP=6时,点P在 ;当 OP 时点 P 在圆内;
当 OP 时,点P不在圆外。
3. 已知 AB =6 cm,画半径为 4 cm 的圆,使它经过 A, B 两点. 这样的圆能画出多少个?如果半径为 3 cm,2 cm 呢?
4. 思考:经过三个已知点 A,B,C 作圆.
【参考答案】
1. 答:(1)点 P 在⊙O 的内; (2)点 P 在⊙O 的上;(3)点 P 在⊙O 的外.
2. 答:圆上;<6;≤6.
3. 答:2 个;若半径为 3 cm 能画出 1 个圆;若半径为 2 cm 不能画出圆.
答:如图:
第二课时
【学习目标】
1.定理不在同一条直线上的三个点确定一个圆;
2.三角形的外接圆;圆的内接三角形;外心;
3.结合“过同一条直线上的三点不能作圆”介绍反证法.
【课前学习任务】
回顾本章知识结构图,认清本节课所处的位置.
【课上学习任务】
学习任务一:
请同学们画三个点 A,B,C.
答案:两种情况,如下图
学习任务二:
经过不在同一条直线上的三个点 A,B,C 能不能作圆?如果能,如何确定所作圆的圆心?
结论:不在同一条直线上的三个点确定一个圆.
学习任务三:补全概念
学习任务四:
请作出锐角三角形、 直角三角形、 钝角三角形的外接圆. 这些外接圆的圆心在什么位置?
答:锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
学习任务五:
巩固练习
2.小腾家的圆形镜子损坏了,他要定制一个大小相同的新镜子,如何测量镜子的半径?
3.如图,已知 Rt△ABC 中,若∠C=90°,AC=5 cm,BC=12 cm,求△ABC 的外接圆半径.
学习任务六:
假设 命题的结论 不成立, 经过推理得出 矛盾 , 由 矛盾 判定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
学习任务七:
巩固练习
4.判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆( ).
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
答案:√,×,×,√.
5.若一个三角形的外心在一边上,则此三角形的形状为( )
A、锐角三角形 B、直角三角形
C、钝角三角形 D、等边三角形
答案:B.
【作业设计】
1.如图,分别作出锐角三角形、直角三角形和钝角三角形的外接圆,它们外心的位置有什么特点?
2.如图是一名考古学家发现的一块古代车轮的碎片,你能帮他找出这个轮子的半?说出你的理由.
试一试:
请用反证法证明“两直线平行,同位角相等”.
已知:AB∥CD,求证:∠1=∠2.
思考:
经过任意四个点是不是可以作一个圆?
【参考答案】
1.答案:锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
2. 答案:
试一试:
证明:先假设∠1≠∠2,
过点 O 作直线 A’B’,使∠EOB’=∠2.
∴A’B’∥CD (同位角相等,两直线平行)
这样,过点 O 就有两条直线 AB、A’B’都平行 CD,
这与平行公理“过直线外一点有且仅有一条直线与已知直线平行”矛盾.
∴假设∠1≠∠2 不正确,
∴∠1=∠2.
思考:
答:根据我们今天学习的经验,我们应该首先对这四个点的位置关系进行分类,从四点在同一条直线上,四个点中有三个点在同一条直线上另一点不在,四点中任意三点都不在同一条直线上去思考.
四点在同一条直线上,不能作圆;
四点中有三个点在同一条直线上另一点不在,不能作圆;
四点中任意三点都不在同一条直线上,有可能作一个圆,也有可能做不出一个圆.
同课章节目录
