第24章 圆 单元练习题(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册第24章《圆》单元练习题(含答案)
一、单选题
1.如图,一个油桶靠在直立的墙边,量得并且则这个油桶的底面半径是( )
A. B. C. D.
2.在中,AB,CD为两条弦,下列说法:①若,则;②若,则;③若,则弧AB=2弧CD;④若,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,点A、B、C在⊙O上,且∠ACB=100o,则∠α度数为( )
A.160o B.120o C.100o D.80o
4.如图,在⊙O中,CD是直径,AB是弦,AB⊥CD于E,AB=8,OD=5,则CE的长为( )
A.4 B.2 C. D.1
5.如图,内接于,CD是的直径,,则( )
A.70° B.60° C.50° D.40°
6.如图,AB 为⊙O 的直径,点 D 是弧 AC 的中点,过点 D 作 DE⊥AB 于点 E,延长 DE 交⊙O 于点 F,若 AC=12,AE=3,则⊙O 的直径长为( )
A.7.5 B.15
C.16 D.18
7.如图,已知、是的弦,,点C在弦上,连接CO并延长CO交于于点D,,则的度数是( )
A.30° B.40° C.50° D.60°
8.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A.28° B.30° C.36° D.56°
9.如图,⊙O是△ABC的外接圆,将△ABC绕点C顺时针旋转至△EDC,使点E在⊙O上,再将△EDC沿CD翻折,点E恰好与点A重合,已知∠BAC=36°,则∠DCE的度数是( )
A.24 B.27 C.30 D.33
10.下列说法正确的是( )
①近似数精确到十分位;
②在,,,中,最小的是;
③如图所示,在数轴上点所表示的数为;
④用反证法证明命题“一个三角形最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”;
⑤如图,在内一点到这三条边的距离相等,则点是三个角平分线的交点.
A.1 B.2 C.3 D.4
二、填空题
11.某圆的周长是12.56米,那么它的半径是______________,面积是__________.
12.如图,A、B、C是上的点,,垂足为点D,且D为OC的中点,若,则BC的长为___________.
13.如图,、是的弦,过点A的切线交的延长线于点,若,则___________°.
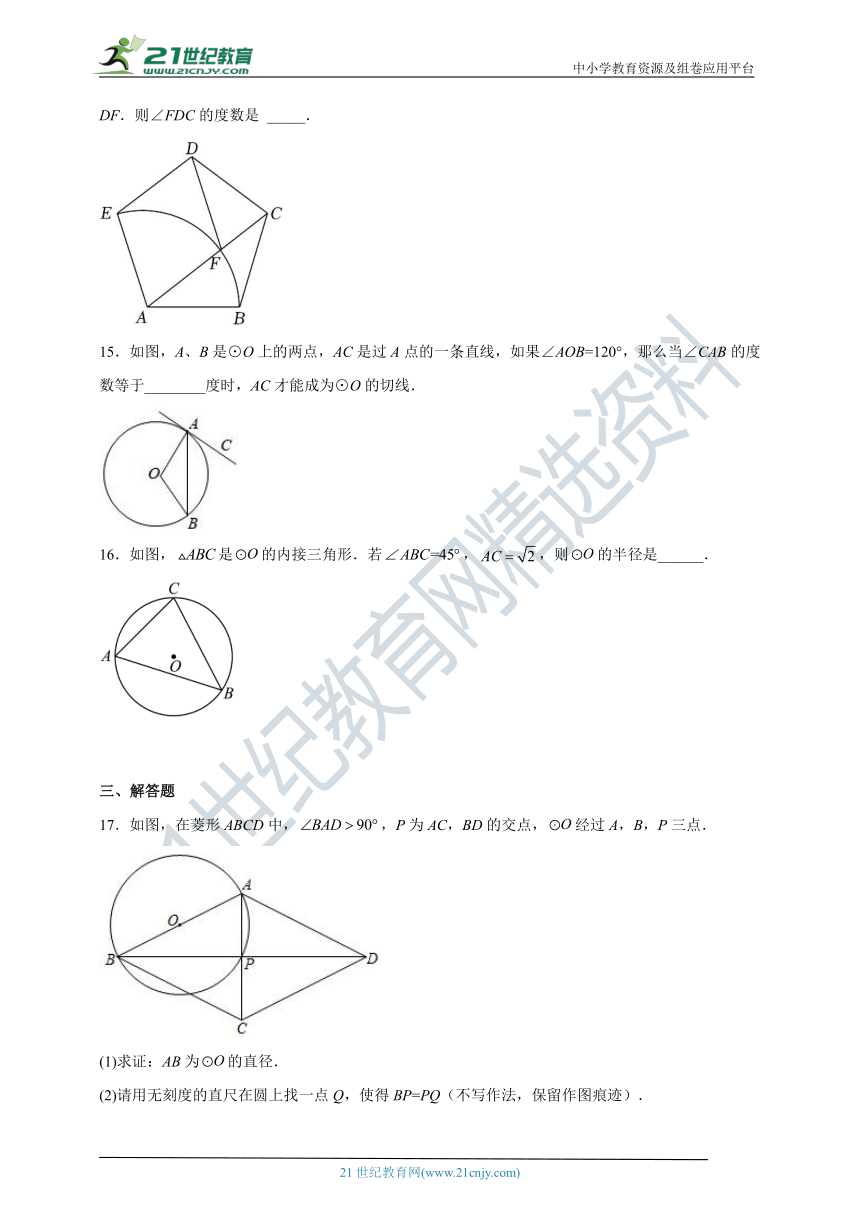
14.如图,在正五边形ABCDE中,连结AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是 _____.
15.如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于________度时,AC才能成为⊙O的切线.
16.如图,是的内接三角形.若,,则的半径是______.
三、解答题
17.如图,在菱形ABCD中,,P为AC,BD的交点,经过A,B,P三点.
(1)求证:AB为的直径.
(2)请用无刻度的直尺在圆上找一点Q,使得BP=PQ(不写作法,保留作图痕迹).
18.请用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:如图,Rt△ABC中,∠C=90°.
求作:一个⊙O,使⊙O与AB、BC所在直线都相切,且圆心O在边AC上.
19.如图所示,AB为⊙O的直径,在△ABC中,AB=BC,AC交⊙O于点D,过点D作DE⊥BC,垂足为点E.
(1)证明DE是⊙O的切线;
(2)AD=8,P为⊙O上一点,P到弦AD的最大距离为8.
①尺规作图作出此时的P点,保留作图痕迹;
②求DE的长.
20.如图,在中,,延长到点,以为直径作,交的延长线于点,延长到点,使.
(1)求证:是的切线;
(2)若,,,求的长.
21.如图,点A,B,C,D在⊙O上,=.求证:AC=BD;
22.如图,点P是的直径延长线上的一点(),点E是线段的中点.在直径上方的圆上作一点C,使得.求证:是的切线.
23.如图,四边形内接于,求证:是等边三角形.
24.如图,四边形ABCD是菱形,以AB为直径作⊙O,交CB于点F,点E在CD上,且CE=CF,连接AE.
(1)求证:AE是⊙O的切线;
(2)连接AC交⊙O于点P,若,BF=1,求⊙O的半径.
25.如图,⊙O是以△ABC的边AC为直径的外接圆,∠ACB=54°,如图所示,D为⊙O上与点B关于AC的对称点,F为劣弧BC上的一点,DF交AC于N点,BD交AC于M点.
(1)求∠DBC的度数;
(2)若F为弧BC的中点,求.
26.已知P为⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有点A、B(不与P、Q重合),连接AP、BP,若∠APQ=∠BPQ
(1)如图1,当∠APQ=45°,AP=1,BP=2时,求⊙O的半径。
(2)如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,设∠NOP=α,∠OPN=β,若AB平行于ON,探究α与β的数量关系。
参考答案
1.C2.A3.A4.B5.C6.B7.C8.A9.B10.B
11. 2米 12.56平方米
12.7
13.35
14.36
15.60
16.1
17(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,即∠APB=90°,
∵经过A,B,P三点.
∴AB为的直径;
(2)解:如图,延长DA交于点Q,即为所求,
理由:连接BQ,
∵AB为的直径,
∴∠AQB=90°,
∴∠BDQ+∠PBQ=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD,
∴∠APB=90°,∠BDQ=∠ABP,
∴∠ABP+∠PBQ=90°,
∵∠ABP+∠BAP=90°,
∴∠BAP=∠PBQ,
∵∠BAP=∠BQP,
∴∠PBQ =∠BQP,
∴BP=PQ.
18.解:作∠ABC的平分线交AC于O点,以O点为圆心,OC为半径作圆,则为所求作的圆.
19.(1)证明:连接OD,BD,
∵AB为⊙O的直径,
∴BD⊥AD,
又∵AB=BC,△ABC是等腰三角形,
∴BD又是AC边上的中线,
∴OD是△ABC的中位线,
∴OD∥BC,又DE⊥BC,
∴DE⊥OD,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)
解:①如图,作AD的垂直平分线与☉O相交于点P,点P即为所求.
②如图,AD的垂直平分线与AD相交于点F,连接BD,
∵PF⊥AD,
∴AF=AD=4,
设☉O的半径为r,
在Rt△AFO中,AF2+FO2=AO2,
即42+(8 r) 2=r2,解得r=5.
∴FO=PF PO=3,
∵FO是△ABD的中位线,
∴BD=2FO=6,
∵AB为⊙O的直径,
∴BD⊥AC,
又∵AB=BC,
△ABC是等腰三角形,
∴AD=DC=8,
∴BC=AB=10,
在Rt△BDC中,
S△BDC=BD CD=BC DE,
∴DE=4.8.
20.(1)如图,连接,
中,,
,
,
,
,
,
,
,
,
即,
是半径,
是的切线;
(2)
如图,过点作,
,
,
,,
,
在与中,
,
,
,
21.证明:∵=,
∴=,
∴,
∴BD=AC.
22.证明:连接,
∵点E是线段的中点,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵是的半径,
∴是的切线.
23.证明:∵四边形内接于,
∴,
又∵,
∴,
∵,
∴,
∴是等边三角形.
24.(1)解:如图所示,连接AF,
∵AB是圆O的直径,
∴∠AFB=90°,
∵四边形ABCD是菱形,
∴AD=AB=CD=BC,∠B=∠D,,
∴∠DAF=∠AFB=90°,
∵CE=CF,
∴CD-CE=BC-CF,即DE=BF,
∴△AED≌△AFB(SAS),
∴∠DAE=∠BAF,
∴∠DAE+∠EAF=90°=∠BAF+∠EAF,
∴∠BAE=90°,
又∵AB是圆O的直径,
∴AE是圆O的切线;
(2)解:如图所示,连接BP,
∵AB是圆O的直径,
∴∠APB=90°,
∵四边形ABCD是菱形,
∴AB=CB,
∴,
设圆O的半径为r,则,
∴,
在Rt△ACF中,,
在Rt△ABF中,,
∴,
解得或(舍去),
∴圆O的半径为.
25.(1)
∵点B、点D关于AC对称,
∴BD⊥AC,
∴∠DBC+∠ACB=90°,
∵∠ACB=54°,
∴∠DBC=90°-54°=36°,
故∠DBC的度数为36°.
(2)
连接OF,
∵点F是的中点,
∴∠BOF=∠COF=2∠BDF,
∵OC=OB,
∴∠OBC=∠OCB=54°,
∴∠OBM=∠OBC-∠DBC=54°-36°=18°,∠BOC=180°-2×54°=72°,
∴∠BOF=∠BOC==36°,
∴∠BDF===18°,
∴∠BDF=∠OBM,
∵点B、点D关于AC对称,
∴DM=BM,
∴在△BOM和△DNM中,
∴△BOM≌△DNM,
∴NM=OM,
∴.
26.(1)连接AB,
∵∠APQ=∠BPQ=45°,
∴∠APB=∠APQ+BPQ=90°,
∴AB是⊙O的直径,
∴AB=,
∴⊙O的半径为;
(2)α+2β=90°,
证明:连接OA、OB、OQ,
∵∠APQ=∠BPQ,
∴,
∴∠AOQ=∠BOQ,
∵OA=OB,
∴OQ⊥AB,
∵ON∥AB,
∴NO⊥OQ,
∴∠NOQ=90°,
∵OP=OQ,
∴∠OPN=∠OQP,
∵∠OPN+∠OQP+∠PON+∠NOQ=180°,
∴2∠OPN+∠PON+∠NOQ=180°,
∴∠NOP+2∠OPN=90°,
∵∠NOP=α,∠OPN=β,
∴α+2β=90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学上册第24章《圆》单元练习题(含答案)
一、单选题
1.如图,一个油桶靠在直立的墙边,量得并且则这个油桶的底面半径是( )
A. B. C. D.
2.在中,AB,CD为两条弦,下列说法:①若,则;②若,则;③若,则弧AB=2弧CD;④若,则.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.如图,点A、B、C在⊙O上,且∠ACB=100o,则∠α度数为( )
A.160o B.120o C.100o D.80o
4.如图,在⊙O中,CD是直径,AB是弦,AB⊥CD于E,AB=8,OD=5,则CE的长为( )
A.4 B.2 C. D.1
5.如图,内接于,CD是的直径,,则( )
A.70° B.60° C.50° D.40°
6.如图,AB 为⊙O 的直径,点 D 是弧 AC 的中点,过点 D 作 DE⊥AB 于点 E,延长 DE 交⊙O 于点 F,若 AC=12,AE=3,则⊙O 的直径长为( )
A.7.5 B.15
C.16 D.18
7.如图,已知、是的弦,,点C在弦上,连接CO并延长CO交于于点D,,则的度数是( )
A.30° B.40° C.50° D.60°
8.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A.28° B.30° C.36° D.56°
9.如图,⊙O是△ABC的外接圆,将△ABC绕点C顺时针旋转至△EDC,使点E在⊙O上,再将△EDC沿CD翻折,点E恰好与点A重合,已知∠BAC=36°,则∠DCE的度数是( )
A.24 B.27 C.30 D.33
10.下列说法正确的是( )
①近似数精确到十分位;
②在,,,中,最小的是;
③如图所示,在数轴上点所表示的数为;
④用反证法证明命题“一个三角形最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”;
⑤如图,在内一点到这三条边的距离相等,则点是三个角平分线的交点.
A.1 B.2 C.3 D.4
二、填空题
11.某圆的周长是12.56米,那么它的半径是______________,面积是__________.
12.如图,A、B、C是上的点,,垂足为点D,且D为OC的中点,若,则BC的长为___________.
13.如图,、是的弦,过点A的切线交的延长线于点,若,则___________°.
14.如图,在正五边形ABCDE中,连结AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是 _____.
15.如图,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于________度时,AC才能成为⊙O的切线.
16.如图,是的内接三角形.若,,则的半径是______.
三、解答题
17.如图,在菱形ABCD中,,P为AC,BD的交点,经过A,B,P三点.
(1)求证:AB为的直径.
(2)请用无刻度的直尺在圆上找一点Q,使得BP=PQ(不写作法,保留作图痕迹).
18.请用圆规、直尺作图,不写作法,但要保留作图痕迹.
已知:如图,Rt△ABC中,∠C=90°.
求作:一个⊙O,使⊙O与AB、BC所在直线都相切,且圆心O在边AC上.
19.如图所示,AB为⊙O的直径,在△ABC中,AB=BC,AC交⊙O于点D,过点D作DE⊥BC,垂足为点E.
(1)证明DE是⊙O的切线;
(2)AD=8,P为⊙O上一点,P到弦AD的最大距离为8.
①尺规作图作出此时的P点,保留作图痕迹;
②求DE的长.
20.如图,在中,,延长到点,以为直径作,交的延长线于点,延长到点,使.
(1)求证:是的切线;
(2)若,,,求的长.
21.如图,点A,B,C,D在⊙O上,=.求证:AC=BD;
22.如图,点P是的直径延长线上的一点(),点E是线段的中点.在直径上方的圆上作一点C,使得.求证:是的切线.
23.如图,四边形内接于,求证:是等边三角形.
24.如图,四边形ABCD是菱形,以AB为直径作⊙O,交CB于点F,点E在CD上,且CE=CF,连接AE.
(1)求证:AE是⊙O的切线;
(2)连接AC交⊙O于点P,若,BF=1,求⊙O的半径.
25.如图,⊙O是以△ABC的边AC为直径的外接圆,∠ACB=54°,如图所示,D为⊙O上与点B关于AC的对称点,F为劣弧BC上的一点,DF交AC于N点,BD交AC于M点.
(1)求∠DBC的度数;
(2)若F为弧BC的中点,求.
26.已知P为⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有点A、B(不与P、Q重合),连接AP、BP,若∠APQ=∠BPQ
(1)如图1,当∠APQ=45°,AP=1,BP=2时,求⊙O的半径。
(2)如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,设∠NOP=α,∠OPN=β,若AB平行于ON,探究α与β的数量关系。
参考答案
1.C2.A3.A4.B5.C6.B7.C8.A9.B10.B
11. 2米 12.56平方米
12.7
13.35
14.36
15.60
16.1
17(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,即∠APB=90°,
∵经过A,B,P三点.
∴AB为的直径;
(2)解:如图,延长DA交于点Q,即为所求,
理由:连接BQ,
∵AB为的直径,
∴∠AQB=90°,
∴∠BDQ+∠PBQ=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,AB=AD,
∴∠APB=90°,∠BDQ=∠ABP,
∴∠ABP+∠PBQ=90°,
∵∠ABP+∠BAP=90°,
∴∠BAP=∠PBQ,
∵∠BAP=∠BQP,
∴∠PBQ =∠BQP,
∴BP=PQ.
18.解:作∠ABC的平分线交AC于O点,以O点为圆心,OC为半径作圆,则为所求作的圆.
19.(1)证明:连接OD,BD,
∵AB为⊙O的直径,
∴BD⊥AD,
又∵AB=BC,△ABC是等腰三角形,
∴BD又是AC边上的中线,
∴OD是△ABC的中位线,
∴OD∥BC,又DE⊥BC,
∴DE⊥OD,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)
解:①如图,作AD的垂直平分线与☉O相交于点P,点P即为所求.
②如图,AD的垂直平分线与AD相交于点F,连接BD,
∵PF⊥AD,
∴AF=AD=4,
设☉O的半径为r,
在Rt△AFO中,AF2+FO2=AO2,
即42+(8 r) 2=r2,解得r=5.
∴FO=PF PO=3,
∵FO是△ABD的中位线,
∴BD=2FO=6,
∵AB为⊙O的直径,
∴BD⊥AC,
又∵AB=BC,
△ABC是等腰三角形,
∴AD=DC=8,
∴BC=AB=10,
在Rt△BDC中,
S△BDC=BD CD=BC DE,
∴DE=4.8.
20.(1)如图,连接,
中,,
,
,
,
,
,
,
,
,
即,
是半径,
是的切线;
(2)
如图,过点作,
,
,
,,
,
在与中,
,
,
,
21.证明:∵=,
∴=,
∴,
∴BD=AC.
22.证明:连接,
∵点E是线段的中点,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵是的半径,
∴是的切线.
23.证明:∵四边形内接于,
∴,
又∵,
∴,
∵,
∴,
∴是等边三角形.
24.(1)解:如图所示,连接AF,
∵AB是圆O的直径,
∴∠AFB=90°,
∵四边形ABCD是菱形,
∴AD=AB=CD=BC,∠B=∠D,,
∴∠DAF=∠AFB=90°,
∵CE=CF,
∴CD-CE=BC-CF,即DE=BF,
∴△AED≌△AFB(SAS),
∴∠DAE=∠BAF,
∴∠DAE+∠EAF=90°=∠BAF+∠EAF,
∴∠BAE=90°,
又∵AB是圆O的直径,
∴AE是圆O的切线;
(2)解:如图所示,连接BP,
∵AB是圆O的直径,
∴∠APB=90°,
∵四边形ABCD是菱形,
∴AB=CB,
∴,
设圆O的半径为r,则,
∴,
在Rt△ACF中,,
在Rt△ABF中,,
∴,
解得或(舍去),
∴圆O的半径为.
25.(1)
∵点B、点D关于AC对称,
∴BD⊥AC,
∴∠DBC+∠ACB=90°,
∵∠ACB=54°,
∴∠DBC=90°-54°=36°,
故∠DBC的度数为36°.
(2)
连接OF,
∵点F是的中点,
∴∠BOF=∠COF=2∠BDF,
∵OC=OB,
∴∠OBC=∠OCB=54°,
∴∠OBM=∠OBC-∠DBC=54°-36°=18°,∠BOC=180°-2×54°=72°,
∴∠BOF=∠BOC==36°,
∴∠BDF===18°,
∴∠BDF=∠OBM,
∵点B、点D关于AC对称,
∴DM=BM,
∴在△BOM和△DNM中,
∴△BOM≌△DNM,
∴NM=OM,
∴.
26.(1)连接AB,
∵∠APQ=∠BPQ=45°,
∴∠APB=∠APQ+BPQ=90°,
∴AB是⊙O的直径,
∴AB=,
∴⊙O的半径为;
(2)α+2β=90°,
证明:连接OA、OB、OQ,
∵∠APQ=∠BPQ,
∴,
∴∠AOQ=∠BOQ,
∵OA=OB,
∴OQ⊥AB,
∵ON∥AB,
∴NO⊥OQ,
∴∠NOQ=90°,
∵OP=OQ,
∴∠OPN=∠OQP,
∵∠OPN+∠OQP+∠PON+∠NOQ=180°,
∴2∠OPN+∠PON+∠NOQ=180°,
∴∠NOP+2∠OPN=90°,
∵∠NOP=α,∠OPN=β,
∴α+2β=90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
